Activité n°2 Expérimentale (Chap.10) : Une boisson rafraîchissante

Titre de l'activité : Activité n°2 Expérimentale (Chap.10) : Une boisson rafraîchissante

Durée : 2 h

Matériels de l'élève

1 calorimètre avec ses accessoires
Balance pour peser les glaçons (d'eau distillée)
Papier absorbant
2 thermomètres numériques ou sonde FOXY sur POD
Bidons d'eau distillée à température ambiante

Compétences

RÉA - Suivre une procédure, un mode opératoire
RÉA - Mesurer
RÉA - Calculer, utiliser une formule
RÉA - Utiliser un outil informatique
APP - Rechercher et extraire l'information
APP - Mobiliser les connaissances en rapport avec le problème
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
COM - Présenter la démarche suivie ou les résultats obtenus à l'aide d'un langage adapté

Notions

Mettre en œuvre un protocole expérimental pour déterminer une énergie mise en jeu lors d'un changement d'état.
Établir un bilan d'énergie pour déterminer une température d'équilibre lors d'un changement d'état

Contexte

C’est l’été, la température extérieure est de $33\ \mathrm{^\circ C}$. Jade souhaite boire une boisson fraîche mais la bouteille n’était pas au frigo. Elle souhaite que la boisson est une température de $6\ \mathrm{^\circ C}$. Pour cela elle dispose de glaçons dans son congélateur à $-18\ \mathrm{^\circ C}$ qui ont une masse de $5\ g$.

Combien devra-t-elle utiliser de glaçons pour rafraîchir $150 mL$ de boisson ?

Définition : Enthalpie de changement d'état (À savoir)

L'enthalpie de changement d'état d'un corps pur est la variation d'enthalpie qui accompagne un changement d'état du corps rapportée à la masse mise en jeu lors de cette transformation. Par exemple pour le passage de l'état liquide à l'état de vapeur on parlera d'enthalpie de vaporisation $L_{vap}$.

L'énergie échangée sous forme de transfert thermique (à température constante) se détermine avec :

\[\fbox{$ {\Large {Q = m\times L } } $}\]

Avec :

$Q$ : Énergie échangée sous forme de transfert thermique $\left(en \; J\right)$
$m$ : masse du corps $\left(en \; kg\right)$
$L$ : Enthalpie de changement d'état $(en \; J.kg^{-1})$

La chaleur latente (ou énergie) de changement d'état L est l'énergie qu'il faut apportée à 1 kg de ce corps pour qu'il change d'état.

Complément : Quelques enthalpies de changement d'état [Document 1]

Substance	Enthalpie de fusion $L_{fus} \ \ \left(\mathrm{kJ/kg} \right)$	Température de fusion $\mathrm{^\circ C}$	Enthalpie de vaporisation $L_{vap} \ \ \left(\mathrm{kJ/kg} \right)$	Température d’ébullition $\mathrm{^\circ C}$
Éthanol	108,00	−114,00	855,00	78,30
Ammoniac	332,17	−77,74	1 369,00	−33,34
Eau	333,55	0,00	2 264,76	100,00
Réfrigérant R134a			215,90	−26,60
Réfrigérant R152a			326,50	−25,00

Complément : Capacité thermique massique de l'eau sous différentes phases [Document 2]

Substance	Phase	Capacité thermique massique $\left(\mathrm{kJ/kg/K} \right)$
Eau	gaz	1,850
	liquide	4,185
	solide	2,060

Définition : Capacité thermique massique d'un corps (Rappels) [Document 3]

Lorsque la température d'un corps solide ou liquide varie d'une valeur initiale $\theta_i$ à une valeur finale $\theta_f$, la quantité de chaleur $Q$ (ou énergie thermique) transférée, égale à la variation d'énergie interne $\Delta U$, est définie par :

\[\fbox{$ \begin{array}{rll} {\Large {\Delta U = Q}} & = & {\Large {m\cdot c\cdot \left ( \theta_f - \theta_i \right ) } } \\ & = & {\Large {m\cdot c\cdot \Delta \theta } } \end{array} $}\]

Avec :

$\Delta U$ : variation d'énergie interne $\left(en \; J\right)$
$m$ : masse du corps $\left(en \; kg\right)$
$c$ : capacité thermique massique $(en \; J.kg^{-1}.^\circ \text{C }^{-1}$ ou $\; J.kg^{-1}.K^{-1} )$
$\Delta \theta$ : variation de température $\left(en \; ^\circ \text{C } ou \; K\right)$

La capacité thermique massique du corps est l'énergie qu'il faut apportée à 1 kg de ce corps pour élever sa température de $1^\circ \text{C}$ (ou de $1\ K$).

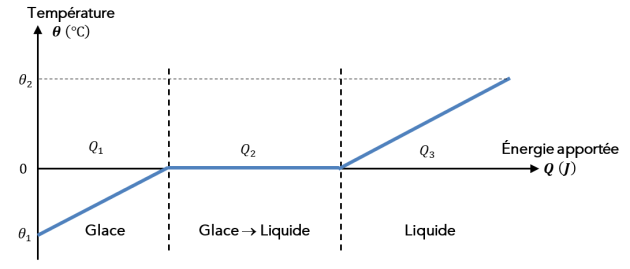
Complément : Évolution de la température en fonction de l'énergie apportée Q à une masse m d'eau [Document 4]

L'évolution de la température en fonction de l'énergie apportée $Q$ à une masse m d'eau initialement sous forme de glace à la température $\theta_1$ qui se transforme en eau liquide à la température $\theta_2$ est donné sur le graphique ci-dessous :

Premiers pas ⚓

Question⚓

Q1. Quel est l’état initial ($T$, $p$, état) de la boisson ? et son état final ?

Solution ⚓

Activité n°2 - Q1.

État initial : ($33\ \mathrm{^\circ C}$, $p_{atm}=10^5\ Pa$, liquide)

État final : ($6\ \mathrm{^\circ C}$, $p_{atm}=10^5\ Pa$, liquide)

Question⚓

Q2. Quel est l’état initial ($T$, $p$, état) du glaçon ? et son état final ?

Solution ⚓

Q2. État initial : ($-18\ \mathrm{^\circ C}$, $p_{atm}=10^5\ Pa$, solide)

État final : ($6\ \mathrm{^\circ C}$, $p_{atm}=10^5\ Pa$, liquide)

(Attention : ici il faut bien considérer que les glaçons ont fondu, et qu'ils sont devenu de l'eau liquide, on parlera d'eau de fonte des glaçons, mais cette eau aura la même masse que celle des glaçons solide !)

Question⚓

Q3. Réaliser un schéma décrivant les différents états intermédiaires du glaçon afin de passer de l’état initial à l’état final ? Écrire les explications de ces différentes étapes.

Solution ⚓

Q3.

Les glaçons solide $-18\ \mathrm{^\circ C}$ doit d'abord se réchauffer et donc gagner de l’énergie thermique pour atteindre la température de fusion $0\ \mathrm{^\circ C}$ de l'eau.
Une fois à $0\ \mathrm{^\circ C}$, les glaçons vont subir le changement d'état « fusion^[*] » et se transformer en eau liquide, et ce à température constante ! Il faut donc qu'ils gagnent de l'énergie thermique qui ne servira qu'au changement d'état.
Une fois entièrement fondu (il n'y aura plus de glaçon solide), l'eau de fonte va devoir se réchauffer et donc gagner de l'énergie thermique pour atteindre la température voulue de $6\ \mathrm{^\circ C}$.

Question⚓

Q4. Quelle est la variation de l’énergie interne du glaçon ? et de la boisson ? Quelle hypothèse faites-vous sur la boisson ?

Ne pas faire de calculs ici.

Donner (en plus des explications) seulement les formules de calculs des variations d'énergie interne demandées. (Ne pas écrire ici les formules des différents transferts thermiques, ce sera à la question Q7 qu'il faudra le faire).

Solution ⚓

Q4.

L'énergie interne du glaçon varie car on doit lui fournir de l'énergie thermique lors des 3 étapes décrites précédemment.

Les glaçons solides reçoivent une énergie $Q_1$ pour passer de la température $\theta_1 = -18\ \mathrm{^\circ C}$ à la température de $\theta_2 = 0\ \mathrm{^\circ C}$.
Les glaçons vont fondre totalement et devenir entièrement liquide, à la température constante de $\theta_2 = 0\ \mathrm{^\circ C}$, en recevant une énergie thermique $Q_2$.
L'eau de fonte des glaçons va se réchauffer et gagner une énergie thermique $Q_3$ pour passer de $\theta_2 =0\ \mathrm{^\circ C}$ à $\theta_f =6\ \mathrm{^\circ C}$

La variation d'énergie interne des glaçons s'exprime donc : $\mathrm {\Delta U_{\text{glaçons} }=Q_1 + Q_2 + Q_3}$.

L'énergie interne de la boisson va aussi varier puisqu'elle va être refroidie par les glaçons. Elle va donc perdre une énergie thermique $Q_4$ pour passer de $\theta_4 =33\ \mathrm{^\circ C}$ à $\theta_f =6\ \mathrm{^\circ C}$.

On aura donc : $\mathrm {\Delta U_{\text{boisson} }=Q_4}$.

Il faut donc considérer la boisson comme n'étant constituée que d'eau.

Détermination expérimentale de l'enthalpie de fusion de l'eau ⚓

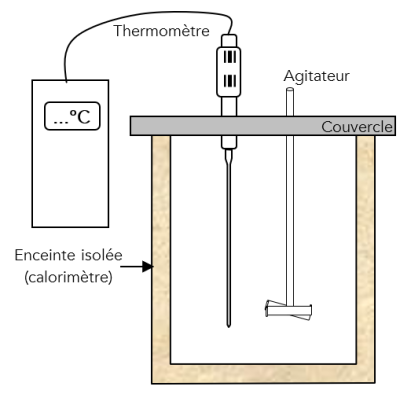
Complément : Le calorimètre [Document 5]

La quantité d'énergie échangée par le calorimètre sera calculée en utilisant sa capacité calorifique $C_{calo} \; \left( \text{en } J.\mathrm{^\circ C}^{-1} \right)$ déterminée lors d'une activité expérimentale précédente.

Il faudra demander au professeur la valeur de $C_{calo}$ à prendre pour votre calorimètre

Rappel :

Si plusieurs corps sont placés dans une enceinte isolée de l'extérieur (enceinte adiabatique), les chaleurs qu'ils reçoivent, dans cette enceinte, vérifient le principe de conservation de l'énergie : soit $\sum{Q_i=0}$

Où $Q_i$ désigne la chaleur reçue par un corps placé à l'intérieur de l'enceinte.

Question⚓

Q5. Voici un protocole expérimental incomplet. Le compléter et l'accompagner d’un schéma) afin de déterminer l'enthalpie de fusion de l'eau.

Introduire $300\ mL$ d'eau dans le calorimètre (masse $m=300g$). Il faudra déterminer très précisément la masse d'eau dans le calorimètre.

Mesurer la température $\theta_1$ de l'eau (et du calorimètre) une fois l'équilibre thermique atteint ${\color{red} \theta_1=}$
Prélever des glaçons fondants (environ $70\ g$) à la température $\theta_2=0\ \mathrm{^\circ C}$ et mesurer rapidement la masse totale de la glace $m_2$.

Introduire les glaçons séchés dans le calorimètre. Agiter.
Mesurer la température finale $\theta_{eq}$ lorsque l'équilibre thermique est atteint ${\color{red} \theta_{eq}=}$

Solution ⚓

Q5.

Exploitation des mesures expérimentales ⚓

Question⚓

Q6. Exprimer la quantité de chaleur $Q_1$ reçue par le glaçon pour se transformer en eau liquide en fonction de $m_2$ et de$ L_{fus}$.

Solution ⚓

Q6. $Q_1=m_2\times L_{fus}$

Question⚓

Q7. Exprimer la quantité de chaleur $Q_2$ reçue par l'eau liquide issue du glaçon pour se réchauffer à la température $\theta_{eq}$ en fonction de $m_2$ , $c_{e,\ell}$, $\theta_2$ et $\theta_{eq}$.

Solution ⚓

Q7. $Q_2=m_2\times c_{e,\ell}\times\left(\theta_{eq}-\theta_2\right)$

Question⚓

Q8. Exprimer la quantité de chaleur $Q_3$ cédée par les $300\ mL$ d'eau lorsqu'elle se refroidit de $\theta_1$ à $\theta_{eq}$.

Solution ⚓

Q8. $Q_3=m_1\times c_{e,\ell}\times\left(\theta_{eq}-\theta_1\right)$

Question⚓

Q9. Exprimer la quantité de chaleur $Q_4$ cédée par le calorimètre lorsqu'il se refroidit de $\theta_1$ à $\theta_{eq}$

Solution ⚓

Q9. $Q_4=C_{calo}\times\left(\theta_{eq}-\theta_1\right)$

Question⚓

Q10. Quelle relation existe-t-il entre $Q_1$, $Q_2$, $Q_3$ et $Q_4$ ? Justifier.

Solution ⚓

Q10. Comme le système {eau + glaçon + calorimètre} est isolé, donc il n'y a aucun échange d'énergie avec l'extérieur, la variation d'énergie interne est nulle : $\Delta U=0=Q_1+Q_2+Q_3+Q_4$

Question⚓

Q11. En déduire l'expression de $L_{fus}$ puis calculer sa valeur.

Solution ⚓

Q11.

$m_2\times L_{fus}+m_2\times c_{e,\ell}\times\left(\theta_{eq}-\theta_2\right)+m_1\times c_{e,\ell}\times\left(\theta_{eq}-\theta_1\right)+C_{calo}\times\left(\theta_{eq}-\theta_1\right)=0$

$m_2\times L_{fus}=-m_2\times c_{e,\ell}\times\left(\theta_{eq}-\theta_2\right)-m_1\times c_{e,\ell}\times\left(\theta_{eq}-\theta_1\right)-C_{calo}\times\left(\theta_{eq}-\theta_1\right)$

$L_{fus}=\dfrac{-m_2\times c_{e,\ell}\times\left(\theta_{eq}-\theta_2\right)-m_1\times c_{e,\ell}\times\left(\theta_{eq}-\theta_1\right)-C_{calo}\times\left(\theta_{eq}-\theta_1\right)}{m_2}$

$L_{fus}=$

Complément : Incertitude relative d'une mesure : r [Document 6]

L'incertitude relative, ou écart relatif, est un indicateur de la qualité et de la précision de la mesure.

Lorsque la grandeur mesurée $m$ possède une valeur de référence connue (théorique), on calcule l'incertitude relative ainsi :

\[\fbox{$ \begin{array}{c} {\Large{ r = \frac{\left| \, m - m_{\text{référence}}\, \right|} {m_{\text{référence}}} } } \end{array} $}\]

Les incertitudes relatives sont en général exprimées en pourcentage, il faudra donc l'écrire en pourcentage.

Plus r est petit et plus la mesure est précise.

On considère que si $r<0,01$ (soit $r<1\, \%$) la mesure est de bonne qualité.

Question⚓

Q12. Comparer à la valeur attendue $L_{fus,\ th}=334\ kJ.kg^{-1}$ en déterminant l'écart relatif. Commenter

Solution ⚓

Q12. Écart relatif :

$r=\dfrac{\left|L_{fus}-L_{fus,\ th}\right|}{L_{fus,\ th}}=$

+ Commentaire à rédiger quand la valeur est calculée.

Retour sur la boisson de Jade ⚓

Question⚓

On suppose de système {boisson+glaçons} est est isolé (adiabatique)^[*].

Q13. Combien faut-il alors de glaçons pour rafraîchir la boisson de Jade ?

Il faut réutiliser les réponses de la question Q4 en détaillant cette fois-ci toutes les formules des transferts thermiques.

Solution ⚓

Q13. On suppose ici que le système {boisson+glaçons} est isolé (adiabatique)^[*] et donc n'échange pas d’énergie avec le milieu extérieur.

Toute l'énergie perdue par la boisson est intégralement transférée aux glaçons (qui se réchauffent, fondent, puis (l'eau de fonte) se réchauffe encore), il n'y a pas de transferts avec le milieu extérieur, donc on a $\mathrm {\Delta U_{\text{système} }=Q_1 + Q_2 + Q_3+Q_4=0}$.

Avec :

${\color{red} Q_1=m_{\text{glaçons} } \times c_{eau, s}\times \left(\theta_2 -\theta_1 \right )=- m_{\text{glaçons} } \times c_{eau, s}\times \theta_1}$ car $\theta_2=0\mathrm{^\circ C}$

${\color{blue} Q_2=m_{\text{glaçons} } \times L_{fus, eau}}$

${\color{green} Q_3=m_{\text{glaçons} } \times c_{eau, \ell}\times \left(\theta_f -\theta_2 \right )=m_{\text{glaçons} } \times c_{eau, \ell}\times \theta_f }$ car $\theta_2=0\mathrm{^\circ C}$

${\color{cyan}Q_4=m_{\text{boisson} } \times c_{eau, \ell}\times \left(\theta_f -\theta_4 \right )}$

$Q_1 + Q_2 + Q_3+Q_4=0$

\[\begin{array}{rll} \large { {\color{red} Q_1} + {\color{blue} Q_2 }+ {\color{green} Q_3}+{\color{cyan} Q_4}=0 } & \Longleftrightarrow & \large { {\color{red} - m_{\text{glaçons} } \times c_{eau, s}\times \theta_1} + {\color{blue} m_{\text{glaçons} } \times L_{fus, eau} } } \\ & & \large { \text{ } + {\color{green} m_{\text{glaçons} } \times c_{eau, \ell}\times \left(\theta_f -\theta_2 \right ) } + {\color{cyan} m_{\text{boisson} } \times c_{eau, \ell}\times \left(\theta_f -\theta_4 \right ) } =0 } \\ & & \large { \text{ } } \\ & \Longleftrightarrow & \large { m_{\text{glaçons} } \times \left ( {\color{red} - c_{eau, s}\times \theta_1} + {\color{blue} L_{fus, eau} } + {\color{green} c_{eau, \ell}\times \theta_f } \right ) = - {\color{cyan} m_{\text{boisson} } \times c_{eau, \ell}\times \left(\theta_f -\theta_4 \right ) } } \\ & \Longleftrightarrow & \large { m_{\text{glaçons} } = \dfrac{ - {\color{cyan} m_{\text{boisson} } \times c_{eau, \ell}\times \left(\theta_f -\theta_4 \right ) } } { {\color{red}- c_{eau, s}\times \theta_1} + {\color{blue} L_{fus, eau} } + {\color{green} c_{eau, \ell}\times \theta_f } } } \\ & \Longleftrightarrow & \large { m_{\text{glaçons} } = \dfrac{ - {\color{cyan} 0,150 } \times 4,185\cdot 10^{3} \times \left(6,0 - 33 \right ) } { {\color{red} - 2,060\cdot 10^{3} \times (-18) } + {\color{blue} 334\cdot 10^{3} } + {\color{green} 4,185 \cdot 10^{3} \times 6,0 } } } \\ & \Longleftrightarrow & \large {{\color{magenta} m_{\text{glaçons} } = 4,3 \cdot 10^{-2}\ kg }} \\ & \Longleftrightarrow & \large {{\color{magenta} m_{\text{glaçons} } = 43\ g }} \end{array}\]

Ce qui représente un nombre de glaçons de :

$N_{\text{glaçons}}=\dfrac{m_{\text{glaçons} }}{m_{\text{1 glaçon} }}=\dfrac{43}{5}=8,6\approx 9$ glaçons.

Glossaire

Adiabatique
Une transformation adiabatique (ou processus adiabatique) est une transformation qui ne produit pas d'échange de chaleur avec le milieu extérieur $\left (Q = 0\right )$.
Ce type de transformation a lieu lorsque le système thermodynamique (dans ce cas un gaz parfait) se trouve dans un récipient isolé de l'extérieur par l'intermédiaire de parois adiabatiques. Les transformations qui se produisent très rapidement et pour lesquelles le système n'a pas le temps d'échanger de la chaleur avec le milieu extérieur peuvent elles aussi être considérées comme étant adiabatiques.
Fusion
C'est le nom du changement d'état de l'état solide à l'état liquide. Rappel : lors d'un changement d'état la température reste constante.
Il s'agit d'une transformation physique.