📑 Documents et définitions⚓
Complément : Le modèle du gaz parfait
Ce modèle a été développé du milieu du XVIIème siècle au milieu du XVIIIème siècle et formalisé au XIXème siècle. Il est fondé sur l'observation expérimentale selon laquelle tous les gaz tendent vers ce comportement à pression suffisamment basse, quelle que soit la nature chimique du gaz, ce qu'exprime la loi d'Avogadro, énoncée en 1811 : la relation entre la pression, le volume et la température est, dans ces conditions, indépendante de la nature du gaz. Cette propriété s'explique par le fait que lorsque la pression est faible, les molécules de gaz sont suffisamment éloignées les unes des autres pour que l'on puisse négliger les interactions électrostatiques qui dépendent, elles, de la nature du gaz (molécules plus ou moins polaires). De nombreux gaz réels vérifient avec une excellente approximation le modèle du gaz parfait dans les conditions normales. C'est le cas des gaz principaux de l'air, le diazote et le dioxygène.
Source : Wikipedia
Complément : Situations de la vie courante
Si l'on place un ballon partiellement dégonflé au soleil, on remarque qu'il reprend son volume initial et qu'il est plus dur.
Le volume d'un gaz contenu dans un ballon augmente avec la température.
La pression d'un gaz augmente avec la température.
Lorsqu'on gonfle un ballon, sa pression augmente.
Il devient plus dur. Gonfler un ballon consiste à introduire de l'air dans le ballon.
Définition : Rappels sur les propriétés d'un gaz
La pression d'un gaz augmente avec la quantité de matière du gaz et le volume d'un gaz augmente aussi avec la quantité de matière du gaz.
La température, le volume, la pression et la quantité de matière d'un gaz sont des paramètres influant sur l'état d'un gaz.
Question⚓
Q1. Décrire simplement ce qu'est un gaz parfait.
Solution⚓
A3-Q1.
On appelle gaz parfait un ensemble de molécules sans interaction entre elles en dehors des chocs élastiques. Les molécules ne s'attirent ou ne se repoussent pas, elles ne font que se cogner les unes aux autres.
Les gaz parfaits ne constituent en fait qu'un modèle qui constitue bien souvent une approximation acceptable.
(Info. : D'autres modèles sont possibles dont le plus connu est celui de Van der Waals.)
🧪 Étude des variables d'état⚓
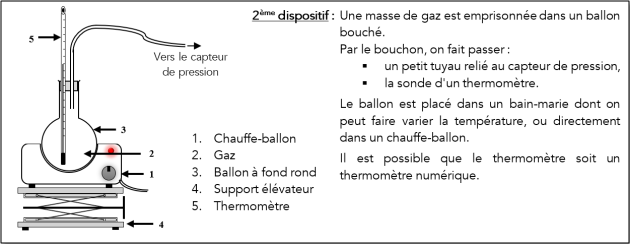
📰 Description du matériel⚓
Question⚓
Q3. À partir de la description du matériel, indiquer les expérimentations qui peuvent être effectuées.
Question⚓
Q4. Pour chaque dispositif préciser les grandeurs qui sont étudiées et celles qui sont maintenus constantes en complétant le tableau ci-dessous :
Grandeurs étudiées | Grandeurs constantes | |
|---|---|---|
1er dispositif | ||
2ème dispositif |
📈 Étude de la relation entre la pression et le volume⚓
Objectif :
Vérifier la relation \(P\times V= \mathrm{Constante}\) à l'aide du dispositif n°1. (\(P\) est la pression absolue)
Le manomètre relié à la seringue mesure une pression différentielle par rapport à la pression atmosphérique.
Il faudra donc penser à utiliser la pression absolue du gaz \(p_{abs}=p_{diff}+p_{atm}\). Un pressiomètre indique la pression atmosphérique lors de l'expérience.
Méthode : Protocole expérimentale à suivre
Relever la valeur de la pression atmosphérique : \(p_{atm}=1034\ \mathrm{hPa}\)
Faire varier le volume autour du volume à l'équilibre pour lequel la pression différentielle est nulle.
Noter alors les valeurs de pression différentielle dans un tableau de mesure.
Calculer alors la pression absolue pour chacune des valeurs de volume mesuré.
Complément : Tableau de mesures
\(V\ \left(\mathrm{en\ mL}\right)\) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
\(p_{diff}\ \left(\mathrm{en\ hPa}\right)\) | |||||||||||
\(p_{abs}\ \left(\mathrm{en\ hPa}\right)\) | |||||||||||
\(p_{abs}\times V\) |
Question⚓
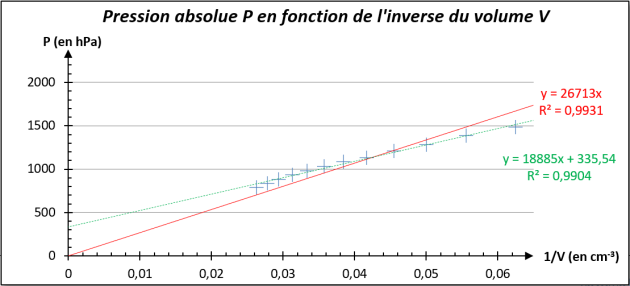
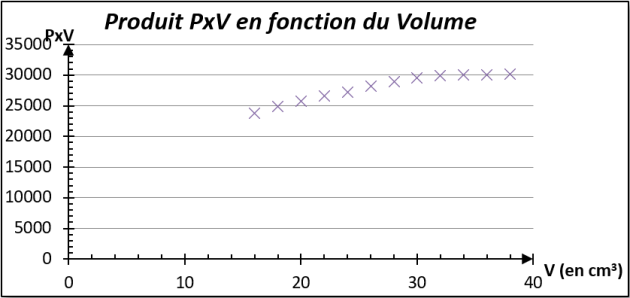
Q6. Quelle type de courbe obtient-on ? Est-ce en accord avec la relation \(P\times V=Cste\) que l'on veut vérifier ? Identifier les sources d'erreurs.
Solution⚓
A3-Q6.
On obtient une droite qui ne passe pas par l'origine comme on devrait avoir car \(P=Cste\times\dfrac{1}{V}\).
Le coefficient de corrélation de la droite qui passe par l'origine (en vert sur mon graphique) n'est pas bon, donc pour nos mesures, on ne peut pas conclure sur une droite qui passe par l'origine.
Les sources d'erreurs possibles se situent d'une part au niveau de la mesure du volume et de la pression qui ne sont pas très précis.
Lors de la mesure du volume, nous n'avons pas tenu compte du volume contenu dans le tuyau.
Question⚓
Q7. Rappeler quelles sont les grandeurs constantes lors de cette expérience. Le sont-elles réellement ? Expliquer.
Solution⚓
A3-Q7.
Les grandeurs censées être constantes sont la quantité de matière et la température.
La température est constante pour la durée de l'expérience, en revanche pour la quantité de matière, c'est moins sûr. En effet, la quantité de gaz contenu dans la seringue peut varier si on appuie ou on tire trop fort le piston de la seringue, car l'étanchéité n'est pas parfaite. Il y a donc des fuites.
C'est ce qui peut expliquer l'écart de nos valeurs par rapport au modèle \(P\times V=Cste\)
Question⚓
Q8. Conclure quant à la validité de la relation \(P\times V=Cste\).
📈 Étude de la relation entre la pression et la température⚓
Méthode : Protocole expérimentale à suivre
Placer le ballon plein d'air sur un chauffe-ballon.
Boucher à l'aide d'un bouchon à deux trous : un trou servant à faire passer un thermomètre et l'autre servant à relier le ballon à un pressiomètre.
Allumer le chauffe-ballon et le régler au maximum.
Chauffer pendant une dizaine de minutes.
Il faudra lire la température \(\theta\) tous les \(5\ \mathrm{^\circ C}\) et en deux temps : d'une part lorsqu'on chauffe le ballon, et d'autre part (si on a du temps) en laissant refroidir le ballon.
Noter les valeurs mesurées dans les tableaux de mesures ci-dessous.
Complément : Tableaux de mesures
\(\theta\ \left(en\ \mathrm{^\circ C}\right)\) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
\(T\ \left(en\ \mathrm{K}\right)\) | |||||||||||
\(p\ \left(\mathrm{en\ kPa}\right)\) |
\(\theta\ \left(en\ \mathrm{^\circ C}\right)\) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
\(T\ \left(en\ \mathrm{K}\right)\) | |||||||||||
\(p\ \left(\mathrm{en\ kPa}\right)\) |
Question⚓
Q10. Proposer puis réaliser une méthode pour déterminer le volume d'air contenu dans le ballon ?
⚠ Appeler le professeur pour faire valider votre méthode ⚠
Solution⚓
A3-Q10.
On remplit le ballon en utilisant de l'eau et une éprouvette graduée. Soit en remplissant totalement le ballon puis en versant l'eau dans une éprouvette (en plusieurs fois si nécessaire). Soit en remplissant le ballon avec l'éprouvette graduée dont on ajoutera les différents volumes nécessaires.
\(V_{ballon}=325\ \mathrm{mL}\)
Question⚓
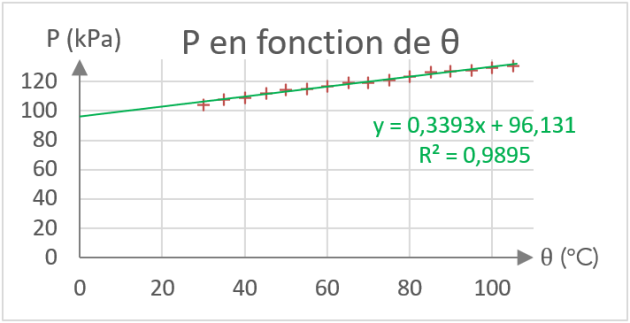
Q11. Il existe une relation simple entre les deux grandeurs \(P\) et \(\theta \ \textsf{ en } \mathrm{^\circ C}\). Tracer un graphique permettant de retrouver cette relation en suivant les consignes suivantes :
Placer la température \(\theta \ \textsf{ en } \mathrm{^\circ C}\) en abscisses.
Faire calculer par le logiciel la courbe de tendance.
Indiquer ci-contre l'allure de la courbe tracée (axes, unités...)
Noter l'équation de la courbe de tendance (appelé également modélisation).
⚠ Appeler le professeur pour faire valider votre méthode ⚠
On définit maintenant la température absolue \(T\) (en Kelvin ou \(K\)) à l'aide de la relation : \(T = 273 + \theta \ \ \ \ \ \left( \ \theta \ \textsf{ en } \mathrm{^\circ C} \ \right)\)
Placer \(T\) en abscisses.
Question⚓
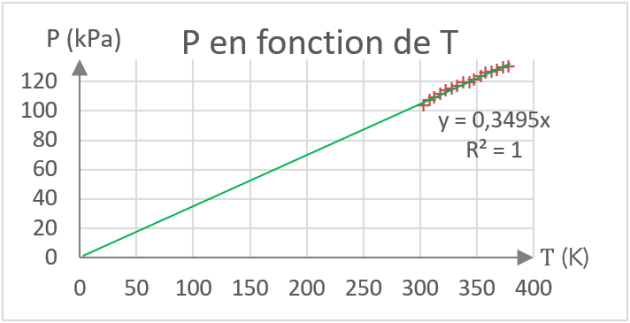
Q12. Tracer un nouveau graphique en suivant les consignes suivantes :
Compléter le tableau avec les valeurs de \(T\ \left(en\ \mathrm{K}\right)\).
Tracer le graphe des variations de la pression en fonction de la température absolue \(K\).
Faire calculer par le logiciel la courbe de tendance.
Indiquer ci-contre l'allure de la courbe tracée (axes, unités...)
Noter l'équation de la courbe de tendance (appelé également modélisation).
⚠ Appeler le professeur pour faire valider votre méthode ⚠
Question⚓
Q13. Quel est l'intérêt de ce changement de variable ? Quand \(P\) tend vers \(0\), que vaut alors \(T\) ?
Par ailleurs, la pression d'un gaz est le résultat de l'agitation des molécules de gaz et des chocs entre les molécules.
Définition :
Le volume \(V\) d'un gaz (pris à une pression et à une température données) est proportionnel au nombre de moles du gaz.
Soit un gaz contenant \(n\) moles et occupant un volume \(V\), sa température absolue est notée \(T\) et sa pression \(P\).
Question⚓
Q15. Parmi les relations suivantes, quelle est celle qui est compatible avec les résultats expérimentaux et le raisonnement du paragraphe précédent.
Dans les équations suivantes, \(a\) est un coefficient de proportionnalité.
\(n=a\times P\times T\times V\)
\(V\ =\ a\times n\times P\times T\)
\(P\ =\ a\times n\times T\times V\)
\(T\ =\ a\times n\times P\times V\)
\(n\times P=a\times P\times V\)
\(n\times T=a\times P\times V\)
\(n\times V=a\times P\times T\)
Définition : L'équation d'état des gaz parfait est :
Où \(\large R\) est La constante des gaz parfaits valant : \(\large R=8,314\ USI\)
D'après l'expression choisie ci-dessus : \(R=\dfrac{1}{a}\).
Définition :
Le gaz parfait est un modèle.
Pour un gaz réel, \(P\times V\approx n\times R\times T\) si la pression est faible et si la température n'est pas trop basse.
Dans les conditions habituelles de température et de pression, l'air (mélange de gaz) se comporte comme un gaz parfait.
Question⚓
Q16. En utilisant l'équation de la courbe de tendance de la Q12. (Pression en fonction de la température absolue), la valeur du volume V et la valeur de R, calculer le nombre n de mole de gaz.
Attention : \(P\ en\ \mathrm{Pa}\ , V\ en\ \mathrm{m^3}\).
Solution⚓
A3-Q16.
Le coefficient directeur de l'équation permet de calculer le nombre de mole de gaz enfermé dans le ballon. Ce coefficient directeur vaut k=0,3495 pour la droite tracée en Q52.
Or cette droite a pour équation \(P=k\times T\),
or comme \(P=\dfrac{n\times R}{V}\times T\) on a alors : \(k=\dfrac{n\times R}{V}\)
Donc : \(n=\dfrac{k\times V}{R}\)
\(n=\dfrac{0,3495\cdot{10}^3\times325\cdot{10}^{-6}}{8,314}\)
\(\color{blue}n=1,37\cdot{10}^{-2}\ \mathrm{mol}\)
🧮 Cas d'un mélange de gaz parfaits⚓
Définition : Définition d'un mélange idéal
Un mélange de gaz parfait est dit idéal quand toutes les particules (qu'elles soient identiques ou non) ne subissent que des chocs élastiques et aucune autre interaction. La pression totale d'un mélange ne dépend alors pas de la nature des gaz présents, mais uniquement de la quantité totale de matière.
Soit un mélange de gaz considérés comme parfait constitué de \(10,0\ \mathrm{g}\) de dioxygène, de \(40,0\ \mathrm{g}\) de diazote et de \(12,0\ \mathrm{g}\) de dioxyde de carbone, occupant un volume total de \(50\ \mathrm{L}\).
Question⚓
Q19. Calculer la quantité de matière totale \(n_\text{total}\) de ce mélange.
Solution⚓
A3-Q19.
Pour appliquer la loi des gaz parfaits, \(P\times V=n_\text{total}\times R\times T\), il faut calculer la quantité de matière totale en gaz présent dans le mélange.
Il nous faut également les masses molaires des molécules :
\(M_{O_2}=2\times M_O=2\times16,0=32,0\ \mathrm{g.mol^{-1}}\) et \(M_{N_2}=2\times M_N=2\times14,0=28,0\ \mathrm{g.mol^{-1}}\)
\(M_{{CO}_2}=M_C+2\times M_O=12,0+2\times16,0=44,0\ \mathrm{g.mol^{-1}}\)
\(n_\text{total}=n_{O_2}+n_{N_2}+n_{{CO}_2}\)
\(n_\text{total}=\dfrac{m_{O_2}}{M_{O_2}}+\dfrac{m_{N_2}}{M_{N_2}}+\dfrac{m_{{CO}_2}}{M_{{CO}_2}}\)
\(n_\text{total}=\dfrac{10,0}{32,0}+\dfrac{40,0}{28,0}+\dfrac{12,0}{44,0}\)
\(\color{blue}n_\text{total}=2,01\ \mathrm{mol}\)
Question⚓
Q20. Calculer alors la pression de ce mélange lorsque la température sera de \(20\ \mathrm{^\circ C}\), et lorsqu'elle sera de \(100 \ \mathrm{^\circ C}\).
Solution⚓
A3-Q20.
Pour une température de de \(20\ \mathrm{^\circ C}\), c'est-à-dire \(20+273=293\) de \(20\ \mathrm{K}\), la pression de ce mélange de gaz sera :
\(P=\dfrac{n_{total}\times R\times T}{V}\)
\(P=\dfrac{2,01\times8,314\times(20+273)}{50\cdot{10}^{-3}}\)
\(\color{blue}P=98,0\ \mathrm{kPa}\)
Pour une température de \(100 \ \mathrm{^\circ C}\), c'est-à-dire \(100+273=393\ \mathrm{K}\), la pression de ce mélange de gaz sera :
\(P=\dfrac{n_\text{total}\times R\times T}{V}\)
\(P=\dfrac{2,01\times8,314\times(100+273)}{50\cdot{10}^{-3}}\)
\(\color{blue}P=1,25\cdot{10}^5\ \mathrm{kPa}\)
Question⚓
Q21. On fixe maintenant la pression à \(1013\ \mathrm{hPa}\) et la température à \(110 \ \mathrm{^\circ C}\). Quel sera le volume occupé par ce mélange de gaz ?
🏋️♂️ Exercices d'entraînement et d'application⚓
💪 Exercice n°1⚓
Calculer le volume occupé à \(20\ \mathrm{^\circ C}\) et pour une pression de \(1,0\cdot{10}^5\ \mathrm{Pa}\) par une masse de \(100\ \mathrm{g}\) de chacun des gaz suivants.
Question⚓
1. L'argon (gaz monoatomique \(\ce{Ar}\)).
Solution⚓
A3-Ex.1-Q1.
Question⚓
2. Le dioxygène \(\ce{O2}\).
Solution⚓
A3-Ex.1-Q2.
Question⚓
3. Le dioxyde de carbone \(\ce{CO2}\).
Solution⚓
A3-Ex.1-Q3.
Question⚓
4. L'hexafluorure de soufre \(\ce{SF6}\).
Solution⚓
A3-Ex.1-Q4.
💪 Exercice n°2⚓
Une bouteille contient du gaz butane \(\ce{C4H10}\) comprimé surmontant du butane liquéfié.
La bouteille est munie d'un manomètre et d'un détendeur.
Question⚓
1. Quels sont les rôles d'un manomètre et d'un détendeur ?
Solution⚓
A3-Ex.2-Q1.
Le manomètre permet de mesurer la pression d'un gaz et le détendeur permet de détendre le gaz.
Il abaisse la pression du gaz comprimé à la pression atmosphérique.
Si le manomètre est placé avant le détendeur, il mesure la pression du gaz à l'intérieur de la bouteille.
Si le manomètre est placé après le détendeur, il mesure la pression du gaz à la sortie de la bouteille.
Question⚓
2. Le contenu de la bouteille a une masse de \(12\ \mathrm{kg}\). Quelle est la quantité de matière correspondante ?
Question⚓
3. En admettant que la totalité du contenu de la bouteille puisse être utilisée sous forme de butane gazeux à \(20\ \mathrm{^\circ C}\) et à la pression atmosphérique de \({10}^5\ \mathrm{Pa}\), quel est le volume de gaz disponible ?
💪 Exercice n°3⚓
On considère deux espèces chimiques gazeuses, puis leur mélange.
On admet que tous les gaz peuvent être modélisés par le gaz parfait.
Une quantité de matière \(n_1\) du premier gaz a un volume \(V_1\), une pression \(p_1\) et une température absolue \(T_1\).
Une quantité de matière \(n_2\) du premier gaz a un volume \(V_2\), une pression \(p_2\) et une température absolue \(T_2\).
Le mélange de ces deux gaz est effectué dans un volume \(V\), la pression et \(p\) et la température absolue \(T\).
Question⚓
3. Dans le cas où \(p=p_1=p_2\) et \(T=T_1=T_2\), déterminer le volume \(V\) du mélange en fonction des volumes \(V_1\) et \(V_2\).
Solution⚓
A3-Ex.3-Q3.
En utilisant les formules du 2. On a :
\(V=\dfrac{n\times R\times T}{p} Avec n=n_1+n_2\)
\(n_1=\dfrac{{p_1\times V}_1}{R\times T_1}\hspace{1cm} \textsf{donc} \hspace{1cm} n_1=\dfrac{{p\times V}_1}{R\times T}\)
\(n_2=\dfrac{{p_2\times V}_2}{R\times T_2} \hspace{1cm} \textsf{donc} \hspace{1cm} n_2=\dfrac{{p\times V}_2}{R\times T}\)
On a donc :
\(V=\dfrac{\left(n_1+n_2\right)\times R\times T}{p}\)
\(V=\left(\dfrac{{p\times V}_1}{R\times T}+\dfrac{{p\times V}_2}{R\times T}\right)\times\dfrac{R\times T}{p}\)
\(\color{blue} V=V_1+V_2\)
Question⚓
4. Dans le cas où \(V=V_1=V_2\) et \(T=T_1=T_2\), établir une relation entre les trois pressions
Solution⚓
A3-Ex.3-Q4.
Pour l'espèce gazeuse 1 : \(p_1\times V=n_1\times R\times T\)
Pour l'espèce gazeuse 2 : \(p_2\times V_2=n_2\times R\times T\)
Pour le mélange : \(p\times V=n\times R\times T\)
\(p=\dfrac{n\times R\times T}{V} \hspace{1cm} \textsf{avec} \hspace{1cm} n=n_1+n_2\)
\(n_1=\dfrac{p_1\times V}{R\times T} \hspace{1cm} \textsf{et} \hspace{1cm} n_2=\dfrac{p_2\times V}{R\times T}\)
Donc :
\(p=\dfrac{\left(\dfrac{p_1\times V}{R\times T}+\dfrac{p_2\times V}{R\times T}\right)\times R\times T}{V}\)
\(\color{blue} p=p_1+p_2\)