Activité n°3 (Chap.2) : La capillarité conséquence de la tension superficielle

🎦 Étude du document vidéo ⚓

Complément : Vidéos à visionner

Flasher le QR-Code ou cliquer sur le lien pour lancer les vidéos

VIDEO 1 - Ascension capillaire et loi de Jurin	VIDEO 2 - Illustration de la loi de Jurin et des conséquences de la capillarité

→ Visionner les deux documentaires vidéo projetés au tableau et répondre aux questions suivantes.

Question⚓

Q1. (ANA) Que fait la tension superficielle lorsqu'on plonge une lame de verre dans de l'eau ?

Solution ⚓

A3-Q1.

Elle va faire monter l'eau sur la paroi du verre.

Question⚓

Q2. (ANA) Comment se nomme le phénomène que l'on observe quand on rapproche deux lames de verre dans l'eau ? Que se passe-t-il lorsqu'on les rapproche davantage ?

Solution ⚓

A3-Q2.

Lorsqu'on rapproche les deux lames de verre, qui chacune élève le niveau de l'eau, on voit apparaître un ménisque. Si on les rapproche encore plus, l'eau s'élève au-dessus du niveau du récipient.

Question⚓

Q3. (ANA) Qui a quantifié le phénomène de monté de liquide entre deux lames de verre très proche ? Quand ?

Solution ⚓

A3-Q3.

C'est James Jurin, au 18^ème siècle.

Question⚓

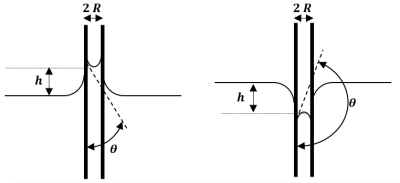
Q4. (APP) De quoi dépend la hauteur $\large h$ de montée du liquide entre les deux parois ?

Solution ⚓

A3-Q4.

La hauteur $\large h$ de montée du liquide dépend de :

La masse volumique $\large \rho$ du fluide
De l'intensité de la pesanteur $\large {g}$
Du coefficient de tension superficielle $\large {\sigma}$
De la distance $\large 2\ R$ qui sépare les deux lames

Question⚓

Q5. (APP) Écrire la relation entre ces paramètres.

Solution ⚓

A3-Q5.

\[\fbox{$ {\large { \color{blue} \text{ } h = \dfrac{2 \times \sigma \times \cos \theta }{\rho \times g \times R} \text{ } }} $}\]

Question⚓

Q7. (APP) Quel paramètre influence le signe de $\large h$ ?

Solution ⚓

A3-Q7.

C'est l'angle de mouillage qui influence le signe de $\large h$.

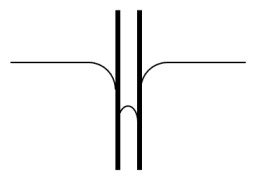
Complément :

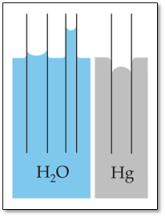
Exemple de remontée capillaire avec l'eau $\large \left( \ H_2O \ \right)$ et de descente capillaire avec le mercure $\large \left( \ Hg \ \right)$ :

Question⚓

Q8. (APP) Comment appelle-t-on le phénomène quand $\large h$ est positif ? Et quand $\large h$ est négatif ?

Solution ⚓

A3-Q8.

Quand $\large h$ est positif on parle d'ascension, et quand $\large h$ est négatif, on parle de dépression capillaire.

Question⚓

Q9. (APP) Quelle doit-être la valeur de l'angle de mouillage $\large \theta$ pour avoir une dépression capillaire avec le mercure ?

Solution ⚓

A3-Q9.

Il faut un angle de mouillage supérieur à $\large {\pi}/{2}$ pour avoir un $\large \cos{\theta}<0$.

Question⚓

Q10. (APP) Cites 7 exemples d'utilisation du phénomène de capillarité ?

Solution ⚓

A3-Q10.

Les éponges (vivantes), et artificielles
Le sopalin™ (papier absorbant)
Le buvard

Le papier filtre utilisé en chromatographie
La mèche des bougies
Remontées d'eau dans les murs (néfaste)
Les plantes

Question⚓

Q11. (ANA) La capillarité est-elle un phénomène tout le temps désirable ? Si non, donner un exemple.

Non, car dans le cas de remontées d'eau dans les murs, cela peut être dangereux, comme ans le cas de l'église Saint Philibert de Dijon qui a dû être fermée au public car les piliers ont été endommagés par des remontées capillaires.

👨‍🎓 Liquide mouillant, et liquide non mouillant : angle de contact ⚓

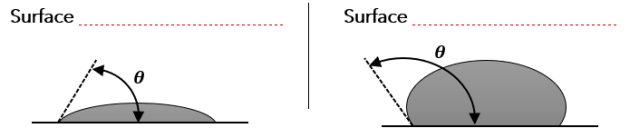
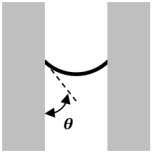
La surface libre d'un liquide est courbe au contact d'une paroi. Ceci est due aux forces capillaires.

L'angle de mouillage $\large \theta$ va déterminer si on a une remontée capillaire $\large \left( \ h>0 \ \right)$ ou un descente capillaire $\large \left( \ h<0 \ \right)$.

Les schémas ci-dessous matérialisent cet angle de mouillage dans le cas d'un tube capillaire et lorsqu'une goutte de liquide est déposée sur une surface.

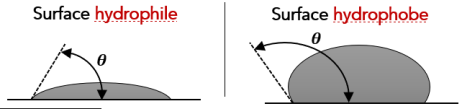
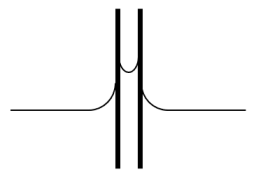
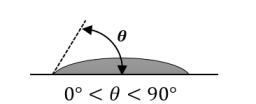
Liquide mouillant

Exemple avec de l'eau et du verre sale

Liquide non mouillant

Exemple avec du mercure et du verre

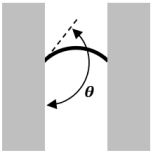
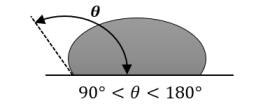
Si l'angle de contact est nul, le liquide mouille parfaitement le solide (exemple : l'eau et du verre propre).

Question⚓

Q12. (APP) Compléter la légende des schémas ci-dessous avec un des mots suivants : hydrophobe, hydrophile.

Solution ⚓

A3-Q12.

👨‍🎓 La loi de Jurin ⚓

Définition : La loi de Jurin (à savoir utiliser, pas à connaître)

\[\fbox{$ {\huge { \color{blue} \text{ } h = \dfrac{2 \ \sigma \ \cos \theta }{\rho \ g \ R} \text{ } }} $}\]

$\large h$ est la hauteur du liquide dans le tube capillaire en mètres $\left(\ \mathrm{m}\ \right)$
$\large \sigma$ est la tension superficielle du liquide en newton par mètre $\left(\mathrm{\ N.m^{-1}\ }\right)$
$\large \rho$ est la masse volumique du liquide en kilogrammes par mètre cube $\left(\mathrm{\ kg.m^{-3}\ }\right)$
$\large \theta$ est l'angle de contact entre le liquide et la paroi du tube en degré $\mathrm{^\circ}$
$\large R$ est le rayon du tube en mètres $\left(\ \mathrm{m}\ \right)$
$\large g$ est l'accélération de la pesanteur terrestre, $g=9,81\ \mathrm{m.s^{-2}}$

💪 Exercices d'application ⚓

Complément : 📄 Données pour faire les exercices

🏋️‍♂️ Exercice n°1 ⚓

On constate de l'humidité (eau) dans un mur jusqu'à une hauteur de $1,2\ \mathrm{m}$.

On estime que le réseau capillaire à un rayon de $1,0\cdot{10}^{-5}\ \mathrm{m}$.

Question⚓

Q13. (RÉA) Déterminer la valeur de l'angle de contact sachant que la température est de $20\ \mathrm{^\circ C}$ ?

Aide : Il faut faire un retournement de formule ; $\theta=\arccos \left(\ \cos \theta \ \right)$

Réponse : $\theta=36 \mathrm{^\circ}$

Solution ⚓

A3-Q13.

\[\begin{array}{rll} \large { h=\frac{2\ \sigma\ cos\ \theta}{\rho\ g\ R} } & {\large \Leftrightarrow} & {\large { cos\ \theta=\dfrac{h\ \rho\ g\ R}{2\ \sigma_\mathrm{eau}} } } \\ & {\large \Leftrightarrow} & {\large { \theta=\arccos\ \left(\dfrac{h\ \rho\ g\ R}{2\ \sigma_{eau}}\right) } } \\ & {\large \Leftrightarrow} & {\large { \theta= \arccos\ \left(\dfrac{1,2\times1000\times9,81\times1,0\cdot{10}^{-5}}{2\times7,28\cdot{10}^{-2}}\right) }} \\ & {\large \Leftrightarrow} & {\large { \theta= \color{blue} 36\ \mathrm{^\circ } }} \end{array}\]

Question⚓

Q14. (RÉA) Même question pour une température est de $0\ \mathrm{^\circ C}$ ?

Réponse : $\theta=39 \mathrm{^\circ}$

Solution ⚓

A3-Q14.

$\large \theta=\arccos\ \left(\dfrac{h\ \rho\ g\ R}{2\ \sigma_{eau}}\right)$

$\large \theta=\arccos\ \left(\dfrac{1,2\times1000\times9,81\times1,0\cdot{10}^{-5}}{2\times7,56\cdot{10}^{-2}}\right)$

$\large \color{blue} \theta=39 \mathrm{^\circ}$

🏋️‍♂️ Exercice n°2 ⚓

L'eau est maintenant dans un tube capillaire en verre dont le rayon est de ${10}^{-3}\ \mathrm{m}$.

Question⚓

Q15. (RÉA) Sachant que la température est maintenant de $0\ \mathrm{^\circ C}$, calculer la hauteur d'ascension de l'eau dans le tube capillaire en verre.

Réponse : $h=15,4\ \mathrm{mm}$

Solution ⚓

A3-Q15.

Pour l'interface eau – verre, l'angle de contact vaut$ \theta=0^\circ$.

$\large h = \dfrac{2 \ \sigma \ \cos \theta }{\rho \ g \ R}$

$\large h =\dfrac{2\times7,56\cdot{10}^{-2}\times \cos\ 0}{1000\times9,81\times{10}^{-3}}$

$\large \color{blue} h =0,0154\ \mathrm{m} = 15,4\ \mathrm{mm}$

Question⚓

Q16. (RÉA) Même question pour une température est de $20\ \mathrm{^\circ C}$.

Réponse : $h=14,8\ \mathrm{mm}$

Solution ⚓

A3-Q16.

On ré-applique la formule de la loi de Jurin avec une nouvelle valeur de $\large \sigma$ :

$\large h =\dfrac{2\times7,28\cdot{10}^{-2}\times \cos\ 0}{1000\times9,81\times{10}^{-3}}$

$\large \color{blue} h =0,0148\ \mathrm{m} = 14,8\ \mathrm{mm}$

Question⚓

Q17. (RÉA) Reprendre les questions Q15. et Q16. avec un tube en paraffine. Commenter.

Réponse : $-4,51\ \mathrm{mm}$ ; $-4,34\ \mathrm{mm}$

Solution ⚓

A3-Q17.

Dans le cas d'un tube en paraffine, on a $\large \theta=107\mathrm{^\circ}$.

À $0\ \mathrm{^\circ C}$ :
$\large h =\dfrac{2\times7,56\cdot{10}^{-2}\times \cos\ 107}{1000\times9,81\times{10}^{-3}}$
$\large \color{blue} h =-0,00451\ \mathrm{m} = -4,51\ \mathrm{mm}$

À $20\ \mathrm{^\circ C}$ :
$\large h =\dfrac{2\times7,28\cdot{10}^{-2}\times \cos\ 107}{1000\times9,81\times{10}^{-3}}$
$\large \color{blue} h =-0,00434\ \mathrm{m} = -4,34\ \mathrm{mm}$

🏋️‍♂️ Exercice n°3 ⚓

On prend maintenant deux lames de verres distantes de $3,0\ \mathrm{mm}$ et de longueur $1\ \mathrm{m}$.

Question⚓

Q18. (RÉA) Calculer la hauteur d'ascension de l'eau ente les deux lames de verre pour une température de $20\ \mathrm{^\circ C}$.

Réponse : $9,9\ \mathrm{mm}$

Solution ⚓

A3-Q18.

$\large h =\dfrac{2\times7,28\cdot{10}^{-2}\times \cos\ 0}{1000\times9,81\times{1,5\cdot 10}^{-3}}$

$\large \color{blue} h =0,0099\ \mathrm{m} = 9,9\ \mathrm{mm}$

🏋️‍♂️ Exercice n°4 ⚓

La sève est principalement constituée d'eau, et le système capillaire des arbres a un rayon de $\large 2,5\cdot{10}^{-5}\ \mathrm{m}$ et que l'on peut considérer que l'angle de contact est nul.

Question⚓

Q19. (RÉA) Calculer la hauteur d'ascension de la sève dans les arbres à une température de $20\ \mathrm{^\circ C}$.

Réponse : $590\ \mathrm{mm}$

Solution ⚓

A3-Q19.

$\large h =\dfrac{2\times7,28\cdot{10}^{-2}\times \cos\ 0}{1000\times9,81\times{2,5\cdot 10}^{-5}}$

$\large \color{blue} h =0,59\ \mathrm{m} = 59\ \mathrm{cm}$

🏋️‍♂️ Exercice n°5 ⚓

On observe des remontées capillaires dans une paroi en bois et ce jusqu'à une hauteur de $\large 80\ \mathrm{cm}$ lorsque la température moyenne est de $\large 20\ \mathrm{^\circ C}$.

Question⚓

Q20. (RÉA) Déterminer le diamètre du système capillaire.

Réponse : $D=38\ \mathrm{\mu m}$

Solution ⚓

A3-Q20.

\[\begin{array}{rll} \large { h=\frac{2\ \sigma\ cos\ \theta}{\rho\ g\ R} } & {\large \Leftrightarrow} & {\large { R=\dfrac{2\ \sigma\ \cos\ \theta}{\rho\ g\ h} } } \\ & {\large \Leftrightarrow} & {\large { R=\dfrac{2\times7,28\cdot{10}^{-2}\times c o s\ 0}{1000\times9,81\times0,80} } } \\ & {\large \Leftrightarrow} & {\large { R= \color{blue} 1,9 \cdot 10^{-5}\ \mathrm{m } }} \end{array}\]

Le diamètre est donc $\large\color{red} D= 2\times R=3,8\cdot{10}^{-5}\ \mathrm{m}$

🏋️‍♂️ Exercice n°6 ⚓

Un liquide mouillant parfaitement le verre et de masse volumique $\large \rho=1,05\cdot{10}^3\ kg.m^{-3}$, s'élève à une hauteur moyenne $\large h=1,5\ cm$ dans un tube capillaire en verre, vertical et de diamètre intérieur $\large d=1,0\ mm$.

Question⚓

Q21. (RÉA) Calculer la constante de tension superficielle du liquide $\left( \ g=9,81\ \mathrm{m.s^{-2}}\ \right)$.

Réponse : $\sigma=3,9\cdot 10^{-2} \ \mathrm{N.m^{-1}}$

Solution ⚓

A3-Q21.

Le liquide est parfaitement mouillant, donc l'angle de contact est nul.

Le rayon du capillaire est $R=\dfrac{d}{2}=\dfrac{1,0}{2}=0,50\ \mathrm{mm}$

\[\begin{array}{rll} \large { h=\frac{2\ \sigma\ cos\ \theta}{\rho\ g\ R} } & {\large \Leftrightarrow} & {\large { \sigma=\dfrac{\rho\ g\ R\ h}{2\ \cos\ \theta} } } \\ & {\large \Leftrightarrow} & {\large { \sigma=\dfrac{1,05\cdot{10}^3\times9,81\times0,50\cdot{10}^{-3}\times1,5\cdot{10}^{-2}}{2\times \cos\ 0} } } \\ & {\large \Leftrightarrow} & {\large { \sigma= \color{blue} 3,9 \cdot 10^{-2}\ \mathrm{N.m^{-1}} }} \end{array}\]