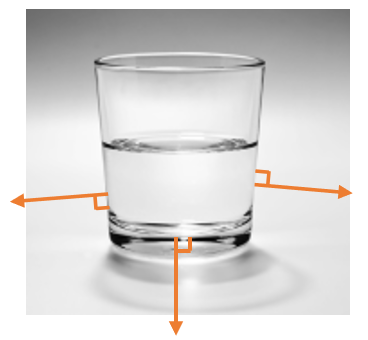
Définition : Force pressante
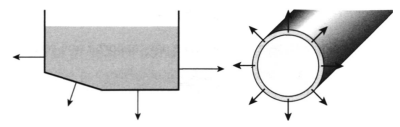
Un gaz ou un liquide contenu dans un récipient exerce une force sur les parois de celui-ci.
Cette force \(\vec{F}\), appelée force pressante, est toujours perpendiculaire aux parois.
Rappel : Représentation d'une force
La force est la grandeur physique associée à l'action mécanique.
Elle se caractérise par :
une direction (une ligne) ;
un sens (sens de parcours de la ligne) ;
une valeur (ou intensité) en newton (N) ;
un point d'application.
Une force localisée est modélisée par un vecteur-force \(\vec{F}\) avec pour point d'application le point de contact.
Une force répartie dans tout le volume (ou en surface) est modélisée par un vecteur-force appliqué au centre d'inertie \(G\) du corps.
Définition : Orientation des forces pressantes
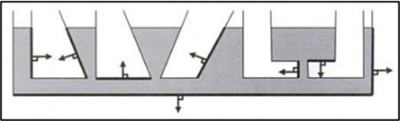
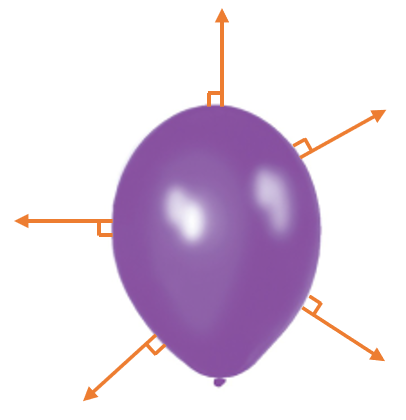
Les forces pressantes sont toujours orientées du fluide vers la paroi, ce qui définit leur sens.
Elles sont perpendiculaires à la paroi, ce qui définit leur direction.
Le point d’application de la force pressante sur une paroi et la valeur de celle-ci dépendent de la façon dont la pression évolue sur cette paroi. Il existe deux cas de figure :
Pression uniforme (la même en tout point de la surface) sur l’ensemble de la paroi :
Exemples : Air ou le vent (un gaz) au niveau d’une cloison verticale, un liquide sur une paroi horizontale.
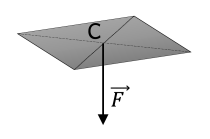
Dans ce cas : \(F = p_\text{rel} \times S\).
Avec \(p_\text{rel} \)la pression relative compte tenu de la hauteur de fluide au-dessus de la surface.
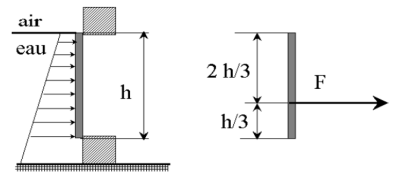
Pression variant linéairement avec la profondeur :
Exemples : Tout fluide incompressible (liquide) sur une paroi verticale.
Dans ce cas : \(F = p_\text{rel\ 1/2} \times S\).
Avec \(p_\text{rel\ 1/2}\) la pression relative à mi-profondeur.
Cette force s’exerce en un point situé à 2/3 de la hauteur de la paroi exposée au fluide incompressible, par rapport à la surface libre.
Représentation de la force pressante dans le cas où la pression est uniforme
Complément : Document n°1 : Lien entre force pressante et pression
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Vidéo sur support numérique.
Attention : Appel professeur
Faites vérifier vos réponses. Expliquer votre choix.
Définition : Unités de la pression
L'unité de la pression dans le système international est le pascal (Pa).
Il existe plusieurs unités de mesures pour la pression. Les trois unités couramment utilisées sont le millimètre de mercure (mmHg), le bar (bar) et le pascal (Pa).
\(1\ \mathrm{bar} = 10^5\ \mathrm{Pa}\)
\(1\ \mathrm{mmHg} = 133\ \mathrm{Pa}\)
La pression atmosphérique, notée \(p_\mathrm{atm}\), correspond à la pression de l'air qui nous entoure. Sa valeur est \(p_\mathrm{atm} \simeq 1,013\ \mathrm{bar} =1013\ \mathrm{hPa} = 101\ 300\ \mathrm{Pa}\).
Question⚓
Q3. (APP/RÉA) Effectuer les conversions suivantes :
Convertir en \(Pa\) :
a. \(2\, bar\)
b. \(3\, mbar\)
c. \(4\, Mbar\)
Convertir en \(bar\) :
d. \(2\,000\, 000\, Pa\)
e. \(2\cdot 10^5\, Pa\)
f. \(3\, kPa\)
Solution⚓
A-Q3.
Convertir en \(Pa\) :
a. \(2\, bar=2\times 10^5 \, Pa\)
b. \(3\, mbar=3\times 10^{-3} \times 10^5 \, Pa\)
\(=3\times 10^{2}\, Pa=300 Pa\)
c. \(4\, Mbar= 4\times 10^{6} \times 10^5 \, Pa\)
\(=4\times 10^{11}\, Pa=400 \ GPa\)
Convertir en \(bar\) :
d. \(2\,000\, 000\, Pa=\dfrac{2\,000\, 000}{10^5}\, bar=20\, bar\)
e. \(2\cdot 10^5\, Pa=\dfrac{2\cdot 10^5}{10^5}\, bar=2\, bar\)
f. \(3\, kPa=\dfrac{3\cdot 10^3}{10^5}\, bar=3\cdot 10^{-2}\, bar=30\, mbar\)
Définition : Force et pression
Q4. (APP) Indiquer ci-dessous la relation entre la force, la pression et la surface pressée avec les unités associées.