Activité n°2 : Masse volumique et densité - [Chap. Densité et masse volumique]

Vous savez tous que la masse d’un litre d’eau est un kilogramme et que si vous portez deux litres d’eau, vous portez deux kilogrammes. Mais pourquoi le savez-vous ? … Parce que vous connaissez déjà tout, ou presque, des grandeurs physiques importantes que sont la masse volumique et la densité.

🔖 Quelques définitions ⚓

Complément : 🎥 Vidéo d’introduction

Considérons un échantillon de matière (dans l’un quelconque de ses trois états : solide, liquide ou gaz) de masse \(m\) et de volume \(V\), et ceci dans des conditions de température et de pression données.

Si la matière est homogène, alors le rapport \(m/V\) est indépendant de l’échantillon prélevé d’une part, et est caractéristique de la nature de la matière considérée d’autre part. Ce rapport caractéristique prend le nom de « masse volumique » et se note généralement « \(\rho\) » (lire « rhô »).

La masse volumique (physique-chimie)

https://ladigitale.dev/digiview/#/v/6396f3a421629

☞ Regarder la vidéo du document précédent, puis répondre aux questions suivantes.

Question⚓

Q1. Compléter la définition de la masse volumique d’un matériau suivante :

Solution ⚓

A2.Q1.

\[\begin{array}{lcl} {\fcolorbox{red}{white}{$ {\Large \color{red}\ \ \ \mathbf{ \rho = \dfrac{m}{V} } \ \ \ } $}} & \textsf{ avec :} & \begin{array}{|lcl} {\large\ \mathbf{m} } & \textsf{:} & { \textsf{masse de l’échantillon en } \large \mathbf{kg} }\\ {\large\ \mathbf{V} } & \textsf{:} & {\textsf{volume occupé par l'échantillon en } \large \mathbf{m^3} } \\ {\large\ \mathbf{\rho} } & \textsf{:} & { \textsf{masse volumique en } \large \color{red}\mathbf{kg.m^{-3}} } \end{array} \end{array}\]

Définition : 📌 La masse volumique

La masse volumique d’un matériau est définie par la relation :

\[\begin{array}{lcl} {\fcolorbox{red}{white}{$ \begin{array}{lcl} {\large\ \hspace{3em} } & \hspace{3em} & { \hspace{2em} } \\ {\large\ \hspace{3em} } & \hspace{3em} & { \hspace{2em} } \\ {\large\ \hspace{3em} } & \hspace{3em} & { \hspace{2em} } \end{array} $}} & \textsf{ avec :} & \begin{array}{|lcl} {\large\ \mathbf{m} } & \textsf{:} & { \textsf{masse de l’échantillon en } \large \mathbf{kg} }\\ {\large\ \mathbf{V} } & \textsf{:} & {\textsf{volume occupé par l'échantillon en } \large \mathbf{m^3} } \\ {\large\ \mathbf{\rho} } & \textsf{:} & { \textsf{masse volumique en } \large \color{red}\textsf{.............} } \end{array} \end{array}\]

Question⚓

Q2. Donner d’autres associations d’unités liant la masse, la masse volumique et le volume.

Solution ⚓

A2.Q2.

Masse en \(\ce{g}\), volume en \(\ce{L}\) :masse volumique en \(\ce{g.L^{-1}}\) ;
Masse en \(\ce{g}\), volume en \(\mathrm{mL}\) : masse volumique en \(\mathrm{g \cdot mL^{-1}}\)

Définition : 📌 Densité d’un matériau

La densité est une grandeur physique sans dimension qui permet de comparer rapidement les masses volumiques entre elles.

\[\begin{array}{lcl} {\fcolorbox{red}{white}{$ {\Large \color{red}\ \ \ \mathbf{ d = \dfrac{\rho}{\rho_{ref}} } \ \ \ } $}} & \textsf{ avec :} & \begin{array}{|lcl} {\large\ \mathbf{d} } & \textsf{:} & { \textsf{densité du matériau, sans unité} }\\ {\large\ \mathbf{\rho} } & \textsf{:} & {\textsf{masse volumique du matériau} } \\ {\large\ \mathbf{\rho_{ref}} } & \textsf{:} & { \textsf{masse volumique de référence} } \end{array} \end{array}\]

Dans le cas des solides et des liquides, le corps choisi pour référence est l’eau (à la température de \(\mathrm{4^\circ C}\) et sous la pression normale \((P=\mathrm{1\ 013\ hPa})\)).
Dans ces conditions, la masse volumique de l’eau vaut :
\(\rho_{eau} \ \mathrm{ \left( 4^\circ C ; 1\ 013\ hPa \right)=999,973\ kg \cdot m^{-3} = 1\ 000\ kg \cdot m^{-3} }\) (avec 4 chiffres significatifs)
Dans le cas des gaz, compte tenu des ordres de grandeur très différents pour les masses volumiques, le corps de référence dans ce cas est également un gaz et il s’agit de l’air, dans les mêmes conditions de température et de pression que le gaz considéré.
Ainsi, dans les Conditions Normales de Température et de Pression, dites conditions « C.N.T.P. » et définies par \(P=\mathrm{1\ 013\ hPa}\) et \(T=\mathrm{273\ K \left( =0^\circ C\right)}\), la masse volumique de l’air est \(\rho_{air} \ \mathrm{ \left( \textsf{C.N.T.P}\right) = 1,292\ 7\ kg \cdot m^{-3} }\), valeur que l’on arrondira souvent à \(\mathrm{ 1,29\ kg \cdot m^{-3} }\) voire \(\mathrm{ 1,29\ kg \cdot m^{-3} }\).

🏋️ Exercices sur la masse volumique et la densité ⚓

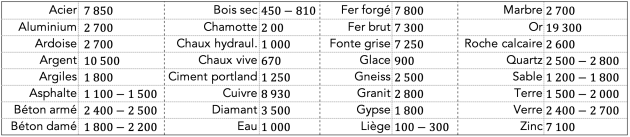
Complément : 📑 Données relatives à tous les exercices

\(P=1\ 000\ \mathrm{bar}\)

\(g=9,81\ \mathrm{N\cdot kg^{-1}}\)

\(d_\mathrm{alcool}=0,8\)

\(d_\mathrm{eau\ de\ mer}=1,03\)

\(\rho_\mathrm{air}=1,3\ \mathrm{kg\cdot m^{-3}}\)

Masses volumiques de quelques corps en \(\mathbf{kg\cdot m^{-3} }\) :

💪 Exercice n°1 : Retournement de formule ⚓

Question⚓

Q3. Exprimer \(m\) en fonction des autres grandeurs.

Solution ⚓

A2.Q3.

\(m=\rho\times V\)

Question⚓

Q4. Exprimer \(V\) en fonction des autres grandeurs.

Solution ⚓

A2.Q4.

\(V=\dfrac{m}{\rho}\)

💪 Exercice n°2 : Calculs de masses volumiques ⚓

Question⚓

Q5. Calculer la masse volumique de l’alcool.

Solution ⚓

A2.Q5.

\(\rho_\mathrm{alcool}=d_\mathrm{alcool}\times\rho_\mathrm{eau}=0,8\times1\ 000=800\ \mathrm{g\cdot L^{-1}} \left( \textsf{ou} =800\ \mathrm{kg\cdot m^{-3}} \right)\)

Question⚓

Q6. Calculer la densité d’un bois de masse volumique \\(rho=750\ \mathrm{g\cdot L^{-1}}\).

Solution ⚓

A2.Q6.

\(d_\mathrm{bois}=\dfrac{\rho}{\rho_\mathrm{eau}}=\dfrac{750}{1\ 000}=0,750\)

💪 Exercice n°3 : Quelques calculs ⚓

Question⚓

Q7. Un bloc de fonte de masse \(m=30\ \mathrm{kg}\) a les dimensions suivantes : \(20\ cm\times20\ cm\times10\ cm\). Déterminer la masse volumique de la fonte.

Solution ⚓

A2.Q7.

\(\rho_\mathrm{fonte}=\dfrac{m}{V}=\dfrac{30}{\left(20\times20\times10\right)\cdot{10}^{-6}}=7\ 500\ \mathrm{kg\cdot m^{-3}}\)

Question⚓

Q8. Déterminer la masse d’un bloc de bois de masse volumique \(\rho=720\ \mathrm{kg\cdot m^{-3}}\) et de dimensions suivantes : longueur \(L=\ 25\ \mathrm{cm}\), largeur \(\ell=10\ \mathrm{cm}\) et hauteur \(h=5,0\ \mathrm{cm}\).

Solution ⚓

A2.Q8.

\(m=\rho\times V=720\times\left(25\times10\times5,0\right)\cdot{10}^{-6}=0,90\ \mathrm{kg}\)

Question⚓

Q9. Remplir le tableau suivant :

Solution ⚓

A2.Q9.

Question⚓

Q10. Calculer la masse du contenu d'une brouette de 60 litres si vous transportez de la chaux vive.

Solution ⚓

A2.Q.

\(m_\mathrm{chaux\ vive}=\rho_\mathrm{chaux\ vive}\times V=670\times60\cdot{10}^{-3}=40\ \mathrm{kg}\)

Question⚓

Q11. Les plaques de laine de verre \(\left(\rho=25\ \mathrm{kg\cdot m^{-3}}\right)\) mesurent \(2,00\ m\) par \(50\ cm\). Quelle sera la masse de 500 plaques de \(5\ cm\) d'épaisseur ?

Solution ⚓

A2.Q11.

\(m_\mathrm{plaques}=500\times m_\mathrm{plaque}\)

\(m_\mathrm{plaques}=500\times\rho\times V\)

\(m_\mathrm{plaques}=500\times25\times2,00\times50\cdot{10}^{-2}\times5\cdot{10}^{-2}\)

\(m_\mathrm{plaques}=6,3\cdot{10}^2\ \mathrm{kg}=0,63\ \mathrm{t}\)

Question⚓

Q12. La densité d’un liquide est de 0,668. En déduire la valeur de sa masse volumique.

Solution ⚓

A2.Q12.

\(\rho=d\times\rho_\mathrm{eau}=0,668\times1\ 000=668\ \mathrm{kg\cdot m^{-3}}\)

Question⚓

Q13. La masse volumique de l’or est de \(19\ 300\ \mathrm{kg\cdot m^{-3}}\). En déduire sa densité puis commenter cette valeur.

Solution ⚓

A2.Q13.

\(d_\mathrm{or}=\dfrac{\rho_\mathrm{or}}{\rho_\mathrm{eau}}=\dfrac{19\ 300}{1\ 000}=19,3\) La densité de l'or est très importante !!

💪 Exercice n°4 : Densité d’un mélange ⚓

Question⚓

Q14. Déterminer la densité d’un mélange constitué de \(50\ \mathrm{L}\) d’eau et \(15\ \mathrm{L}\) d’hydrocarbures (masse volumique égale à \(850\ \mathrm{kg\cdot m^{-3}}\).

(Aide : \(d=0,97\) ; indice : Il faut dans un premier temps déterminer la masse totale, puis le volume total).

Solution ⚓

A2.Q14.

\(m_\mathrm{eau}=\rho_\mathrm{eau}\times V_\mathrm{eau}=1\ 000\times50\cdot{10}^{-3}=50\ \mathrm{kg}\)

\(m_\mathrm{hc}=\rho_\mathrm{hc}\times V_\mathrm{hc}=850\times15\cdot{10}^{-3}=12,75\ \mathrm{kg}\)

\(V_\mathrm{total}=50+15=65\ \mathrm{L}=65\cdot{10}^{-3}\ \mathrm{m^3}\)

\(d_\text{mélange}=\dfrac{\rho_\text{mélange}}{\rho_\text{eau}}=\dfrac{\ \ \ \dfrac{m_\text{mélange}}{V_\text{total}}\ \ \ }{\rho_\text{eau}}=\dfrac{ m_\text{eau} + m_\text{hc} } {V_\text{total} \times \rho_\text{eau} }\)

\(d_\text{mélange}=\dfrac{ 50+ 12,75 } {65\cdot{10}^{-3} \times 1\ 000 }=0,97\)

💪 Exercice n°5 : Questions diverses ⚓

Question⚓

On mélange \(5\ \mathrm{kg}\) d’huile et \(\ce{100\ g}\) d’eau. La masse volumique de l’huile est de \(780\ g/L\).

Q15. Comment se positionnent l’huile et l’eau l’une par rapport à l’autre ?

Solution ⚓

A2.Q15.

L’huile se place au-dessus de l’eau car elle est moins dense que l’eau.

Question⚓

Q16. La masse joue-t-elle un rôle sur la position de corps les uns par rapport aux autres ?

Solution ⚓

A2.Q16.

La masse des corps ne joue aucun rôle quant à la position des uns par rapport aux autres, seule la différence de densité importe. (et le fait que les deux substances ne doivent pas être miscible pour être séparées).

💪 Exercice n°6 : Masse volumique et densité d’un liquide ⚓

Pour mesurer la densité de l’éthanol, on utilise une fiole jaugée de \(50,0\ \mathrm{mL}\). On pèse la fiole vide : \(m_1=53,257\ \mathrm{g}\). On la pèse remplie d’éthanol jusqu’au trait de jauge : \(m_2=92,807\ \mathrm{g}\), à \(20\ \mathrm{^\circ C}\).

Question⚓

Q17. Déterminer la densité de l’éthanol.

(Réponse : \(d=0,791\) ; indice : Il faut dans un premier temps déterminer la masse, puis la masse volumique).

Solution ⚓

A2.Q17.

\(V_\mathrm{eth}=50,0\ \mathrm{mL} \ \textsf{ et } \ m_\mathrm{eth}=m_2-m_1=92,807-53,257=39,550\ \mathrm{g}\)

\(d_{eth}=\dfrac{\rho_{eth}}{\rho_{eau}}=\frac{\ \ \ \dfrac{m_{eth}}{V_{eth}}\ \ \ }{\rho_{eau}}=\dfrac{m_{eth}}{V_{eth}\times\rho_{eau}}=\dfrac{39,550\cdot{10}^{-3}}{50,0\cdot{10}^{-6}\times1\ 000}=0,791\)

Question⚓

Q18. Un baril de diamètre \(D=80,0\ \mathrm{cm}\) et de hauteur \(h=1,20\ \mathrm{m}\) est rempli aux trois-quarts d’huile lubrifiante de densité \(d_\mathrm{h}=0,880\). Déterminer la masse d’huile dans le baril.

(Réponse :\( m=398\ \mathrm{kg}\)).

Solution ⚓

A2.Q18.

\(\definecolor{light_blue}{RGB}{78,173,234}V_h=\dfrac{3}{4}\times\pi\dfrac{D^2}{4}\times h\ \ \ \ \ \ \ \ \color{light_blue}\left( \textsf{Le calcul ici n’est pas utile, la valeur du volume ne nous intéresse pas…}\right)\)

\(m_\mathrm{h}=\rho_\mathrm{h}\times V_\mathrm{h}=d_\mathrm{h}\times\rho_{eau}\times\pi\dfrac{D^2}{4}\times h\)

\(m_\mathrm{h}=0,880\times1\ 000\times\dfrac{3}{4}\times\pi\dfrac{\left(80,0\cdot{10}^{-2}\right)^2}{4}\times1,20=398\ \mathrm{kg}\)

💪 Exercice n°7 : Masse d’air dans une pièce… [Bonus]⚓

Une pièce parallélépipédique a les dimensions suivantes : \(10\ \mathrm{m}\times4,5\ \mathrm{m}\times2,5\ \mathrm{m}\).

Question⚓

Q19. Calculer la masse d’air enfermée dedans.

(Réponse : \(m=1,46\cdot{10}^2\ \mathrm{kg}\)).

Solution ⚓

A2.Q19.

\(m_\mathrm{air}=\rho_\mathrm{air}\times V\text{pièce}= 1,3\times 10\times 4,5\times 2,5=146\ \mathrm{kg}\)