📄 Le théorème d'Archimède expliqué⚓
La loi physique qu'Archimède a théorisé à partir du problème de la couronne[*] s'énonce généralement avec ce théorème :
Définition :
« Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé ; cette force est appelée poussée d'Archimède. »
Question⚓
Q1. Expliquer les 3 mots ou groupes de mots en gras dans la définition précédente.
Solution⚓
Q1.
Un
« corps »
désigne un objet solide d'un volume quelconque.Un
« fluide au repos »
est un liquide ou un gaz immobile. Pour que la poussée d'Archimède puisse s'exercer, il faut en effet que le fluide et le corps soient, tout du moins théoriquement, au repos. Sans cela d'autres forces seront mises en œuvre : si un corps tombe d'une hauteur élevée, à cause de la gravité il va ainsi d'abord s'enfoncer dans l'eau avant de remonter.Pour visualiser la
« force verticale dirigée de bas en haut »
dont il est ici question, il faut simplement imaginer que dans l'eau agit une force (contraire à la gravité, qui est une force verticale dirigée de haut en bas, à cause de laquelle les objets chutent), qui repousse les objets vers la surface.
Question⚓
Q3. En utilisant les informations précédentes, expliquer pourquoi un bateau plongé dans un fluide, l'eau de mer en l'occurrence, ne coule pas lorsqu'il est sur l'eau.

Solution⚓
Q3.
Si ce bateau ne coule pas, jusqu'à toucher le fond de la mer, c'est parce qu'une force verticale agissant de bas en haut le maintient à la surface, et que cette force s'oppose à la force de la gravité, qui attire quant à elle le bateau vers le fond, en agissant de haut en bas.
Ainsi donc, en dépit du poids du corps, qui devrait le pousser à tomber, celui-ci reste en surface : il a atteint un parfait équilibre. Cela signifie tout simplement que le poids du corps est compensé par la poussée exercée par le fluide. C'est la poussée d'Archimède.
🔎 Origine de la poussée d'Archimède⚓
Complément :
📝 (facultatif) Démonstration⚓
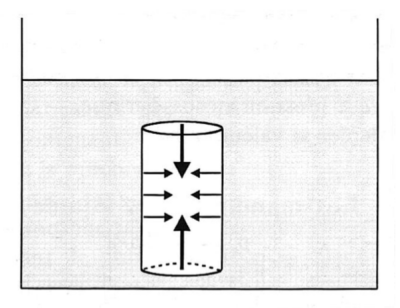
Attention :
Remarque : on ne doit pas considérer les forces pressantes sur les faces latérales, comme celles-ci se compensent mutuellement.
(à rédiger séparément)
Question⚓
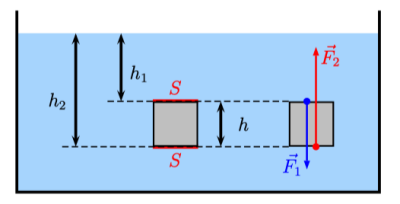
En utilisant le schéma de droite du document précédent, exprimer :
la pression hydrostatique \(p_1\) et \(p_2\) à la profondeur \(h_1\) puis celle en \(h_2\) ;
les forces \(F_1\) et \(F_2\) exercées par le fluide à ses deux profondeurs ;
la différence de ces deux forces.
Comment appelle-t-on cette différence de forces ?
Solution⚓
La face supérieure se trouve à une profondeur \(h_1\), la face inférieure à une profondeur \(h_2\ \left( =h_1 +h \right)\).
La pression hydrostatique à la profondeur \(h_1\), vaut : \(p_1=\rho_\text{liq} \times g \times h_1\)
En \(h_2\), vaut : \(p_2=\rho_\text{liq} \times g \times h_2\).
Le liquide exerce donc la force pressante ascendante \(\vec{F_2}\) sur la face inférieure telle que :
\(F_2=p_2\times S=\rho_\text{liq} \times g \times h_2 \times S\)
De même : La norme de la force pressante descendante \(\vec{F_1}\) exercée par le liquide sur la face supérieure vaut :
\(F_1=p_1\times S=\rho_\text{liq} \times g \times h_1 \times S\)
Comme \(F_2 > F_1\) , le corps est soumis à une force résultante \(\vec{F_A}= \vec{F_1} + \vec{F_2}\) dirigée vers le haut et de norme :
\[\begin{array}{rll} {\large F_A=F_2-F_1 } & {\large = \rho_\text{liq.dépl} \times g \times S \times \left(h_2-h_1 \right) } & \large { | \ \text{ or : } h_2-h_1=h }\\ & {\large = \rho_\text{liq.dépl} \times g \times S \times h } & \large { | \ \text{ or : } S\times h = V }\\ & {\large = \rho_\text{liq.dépl} \times g \times V } \end{array} \mathbf{ }\]
On retrouve la formule de l'expression de la poussée d'Archimède que nous verrons dans le prochain paragraphe.
On peut montrer que cette formule reste valable pour toute autre forme que pourrait avoir le corps immergé.
📌 Énoncé et formule mathématique⚓
Définition : (À SAVOIR 📍)
Tout corps plongé dans un fluide au repos reçoit de la part de ce dernier une force verticale ascendante égale au poids du volume de fluide déplacé par le corps et appliquée au centre de gravité du volume de fluide déplacé, appelée poussée d’Archimède.
Le volume du liquide déplacé est égal au volume du corps \(V_\text{liq.dépl}\).
Question⚓
Q5. Écrire la poussée d'Archimède en fonction du volume de fluide déplacé \(V\), de sa masse volumique \(\rho_\text{liq.dépl}\) et de l'intensité de pesanteur \(g\) ?.
🏋🏻♂️ Petits exercices⚓
💪 Exercice n°1 : Poussée d’Archimède sur un cube de fonte⚓
Un cube de fonte de masse volumique \(\rho= 6\ 700\ \mathrm{kg\cdot m^{-3}}\) et a pour arête : \(80,0\ \mathrm{cm}\).
Question⚓
Q6. Déterminer la poussée d’Archimède exercée sur le cube entièrement immergé dans de l’eau de masse volumique \(\rho_\text{eau}=1\ 000\ \mathrm{kg\cdot m^{-3}}\).
Solution⚓
Q6.
\(P_A = \rho_\text{fluide} \times g \times V_\text{imm.}\)
Le cube est entièrement immergé, donc son \(V_\text{imm.}\) correspond à son volume entier.
\(V_\text{imm.}= a \times a \times a = \left( a \right)^3 =0,8003^3 = 0,512 \ \mathrm{m^{3}}\)
\(P_A= 1\ 000 \times 9,81 \times 0,512 = 5,02\cdot 10^3\ \mathrm{N}\)
💪 Exercice n°2 : Poussée d’Archimède sur un cube de bois⚓
Un cube de bois de masse \(m = 600\ \mathrm{kg}\) a pour arête : \(1,0\ \mathrm{m}\).
Question⚓
Q9. Déterminer la poussée d’Archimède exercée sur le cube entièrement immergé dans de l’eau de densité \(1,01\).
Solution⚓
Q9.
\(P_A = \rho_\text{fluide} \times V_\text{imm.} \times g\)
Le cube est entièrement immergé, donc son \(V_\text{imm.}\) correspond à son volume entier.
\(V_\text{imm.}= a \times a \times a = \left( a \right)^3 =1,0^3 = 1,0 \ \mathrm{m^{-3}}\)
\(P_A= 1\ 010 \times 9,81 \times 1,0= 9,9\cdot 10^3\ \mathrm{N}\)
Question⚓
Q11. En comparant les deux forces, justifier que le cube n’est que partiellement immergé à l’équilibre.
Solution⚓
Q11.
\(P_A > P\) donc le cube remonte. Tant que le cube est entièrement immergé, il continu à remonter car \(P\) et \(P_A\) ne changent pas. Le cube commence donc à sortir de l’eau. Mais dès qu’il sort de l’eau, \(V_\text{imm.}\) diminue donc \(P_A\) aussi.
Tant que \(P_A > P\) , le cube continue à sortir de l’eau et \(V_\text{imm.}\) continue à diminuer, jusqu’à ce que \(P_A = P\). À ce moment, le cube flotte ne sort pas davantage de l'eau : il reste immobile.
Question⚓
Q12. Déterminer le volume immergé du cube.
💪 Exercice n°3 : Poussée d’Archimède sur un élément de tunnel sous-marin⚓
D’après la vidéo sur la construction du tunnel sous-marin reliant Copenhague à Malmö, on peut noter les informations suivantes :
« La réalisation du tunnel nécessite la fabrication avec de l’acier et du béton, de 20 segments ; chacun d’une longueur équivalente à 2 terrains de foot, d’une hauteur équivalente à une maison de 3 étages et ayant une masse de 55 000 tonnes. »
Chaque élément a pour longueur \(L=176 \ \mathrm{m}\), largeur \(\ell=39 \ \mathrm{m}\) et hauteur \(h=8,5 \ \mathrm{m}\)
Chaque élément est obstrué par 2 panneaux d’acier chacun de masse \(m_a = 3\ \mathrm{t}\).
Masse volumique :
du béton : \(2,2\cdot 10^3 \mathrm{kg\cdot m^{-3}} \) ;
de l’acier \(7,5\cdot 10^3 \mathrm{kg\cdot m^{-3}}\) ;
de l’eau de mer \(1,03\cdot 10^3 \mathrm{kg\cdot m^{-3}}\).
Question⚓
Q13. Vérifier par le calcul, que chaque élément flotte effectivement dans l’eau de mer (une fois fermés par les 2 panneaux d’acier).
Solution⚓
Q13.
Masse de chaque segment :
\(M = 55\ 000 \ \mathrm{t}\)
Calcul du poids d’un segment :
\(P = M \times g = 55\ 000\ 000 \times 9,81 = 5,4\cdot 10^8 \ \mathrm{N}\)
Calcul de la Poussée d’Archimède d’un caisson si on suppose qu’il est entièrement immergé :
\(P_A = \rho_\text{fluide} \times g \times V_\text{imm.}\) (\(V_\text{imm.}\) correspond à son volume entier).
\(V_\text{imm.} = 176 \times 39 \times 8,5 = 5,8\cdot 10^4 \ \mathrm{m^3}\)
\(P_A = 1030 \times 9,81 \times 5,8\cdot 10^4 =5,9\cdot 10^8 \ \mathrm{N}\)
Comparaison de P et de \(P_A\) :
On a \(P_A > P\) donc le segment n’est que partiellement immergé, il flotte.
Question⚓
Q14. Déterminer la hauteur d’immersion de chacun des éléments et vérifier que la profondeur de l’eau de mer est suffisante (\(8\ \mathrm{m}\) de tirant d’eau maximum).
Solution⚓
Q14.
Calcul du volume immergé :
Lorsque \(P_A = P\), le cube flotte. Il en vient l’égalité suivante :
\(\rho_\text{fluide} \times g \times V_\text{imm.} = m \times g\)
\(\rho_\text{fluide} \times V_\text{imm.} = m\)
\(V_\text{imm.} = \dfrac{m}{\rho_\text{fluide} } =\dfrac{55\ 000\ 000}{1030 }=5,4\cdot 10^4 \ \mathrm{m^3}\)
Calcul de la hauteur immergé (autrement appelé le tirant d’eau) :
\(V_\text{imm.} = L \times \ell \times h_\text{imm.} = 176 \times 39 × h_\text{imm.}\)
\(h_\text{imm.} = \dfrac {V_\text{imm.} } {L\times \ell }= 7,9 \ \mathrm{m}\)
\(7,9 \ \mathrm{m} < 8 \ \mathrm{m}\), donc le segment peut flotter et naviguer sur le bras de mer.
🧪 Mise en évidence expérimentale⚓
Attention : CCF
Les démarches utilisées dans cette expérience peuvent être demandées en CCF.
🧪 Expérience n°1 : Mesure de la Poussée d’Archimède (1ère méthode)⚓
Question⚓
Q15.
À l’aide du matériel à disposition et du protocole donné ci-dessous, réaliser le montage expérimental permettant de mesurer la valeur du volume de solide immergé \(V\text{imm}\).
Déterminer ensuite par le calcul la valeur de la Poussée d’Archimède \(P_A\) exercée par l’eau sur le corps immergé.
Données :
\(\rho_\text{eau}=1\ 000\ \mathrm{kg\cdot m^{-3}}\) ou \(\rho_\text{eau}=1,000\ \mathrm{kg\cdot L^{-1}}\)
\(g=9,81\ \mathrm{N /kg}\)
Protocole :
Dans une éprouvette graduée, introduire un volume \(V\) très précis d’eau (du robinet).
Noter ce volume : \(V =…………\)
Introduire dans cette éprouvette, une masse marquée retenue par un fil, de telle sorte que la masse soit entièrement immergée.
Noter la masse \(m = …………\)
Noter le nouveau volume d’eau contenu dans l’éprouvette \(V^\prime = …………\)
Déterminer la valeur du volume immergé \(V\text{imm}\) de la masse marquée, en précisant le calcul.
Noter le calcul et le résultat pour le volume \(V\text{imm} = …………\)
Déterminer la valeur de la Poussée d’Archimède \(P_A\) exercée sur le volume immergé.
Noter le calcul et le résultat pour le volume \(P_A = …………\)
🧪 Expérience n°2 : Mesure de la Poussée d’Archimède (2ème méthode)⚓
Complément : Le dynamomètre

Un dynamomètre est un appareil constitué d’un ressort étalonné, qui mesure la force exercée à l’une de ses extrémités. Si on accroche un objet de masse \(m\), le dynamomètre affichera la valeur du poids \(\vec P\) de cet objet.
Question⚓
Q15.
À l’aide du matériel à disposition, notamment d’un dynamomètre, et du cours, proposer un protocole expérimental (celui-ci peut être avantageusement accompagné d’un schéma) permettant de déterminer d’une autre manière la valeur de la Poussée d’Archimède s’exerçant sur un objet immergé dans l’eau.
Réaliser ensuite ce protocole et exploiter vos mesures afin de déterminer la valeur de la Poussée d’Archimède \(P_A\) s’exerçant sur ce corps.