🔖 Qu'est-ce que l'enthalpie de combustion ?⚓
Définition : 📌 Corps simple et corps composés
On appelle corps simple tout constituant formé d’un seul élément chimique. On appelle corps composé tout constituant formé d’au moins deux éléments différents.
Définition : 📌 Enthalpie de formation
On appelle enthalpie de formation \(\Delta_fH^0\) d’un constituant, à la température \(T\) et sous la pression de \(1\ \mathrm{bar}\), l’énergie thermique libérée ou reçue lors de la réaction de formation d’une mole de ce constituant. Elle s’exprime en \(\mathrm{J.mol^{-1}}\).
Par convention, l’enthalpie de formation du corps simple correspondant à son état le plus stable à la température \(T\) et sous la pression de \(1\ \mathrm{bar}\) est nulle.
Lorsque \(\Delta_fH^0>0\), la transformation chimique reçoit de l’énergie.
Lorsque \(\Delta_fH^0<0\), la transformation chimique libère de l’énergie.
Exemple : Exemples d'enthalpies de formation
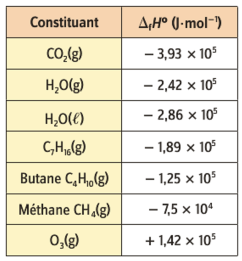
Exemples d'enthalpies de formation à \(25\ \mathrm{^\circ C}\) sous la pression de de \(1\ \mathrm{bar}\). L'état physique du constituant doit être précisé (solide, liquide, gaz).
Définition : 📌 Enthalpie de combustion
On appelle enthalpie de combustion \(\Delta_fH^0\) d’un constituant, à la température \(T\) et sous la pression de \(1\ \mathrm{bar}\), lors de la réaction complète d’une mole de combustible avec le dioxygène. Elle s’exprime en \(\mathrm{J.mol^{-1}}\).
Lors d’une combustion, le système chimique cède de l’énergie au milieu extérieur : les enthalpies de combustion sont de signe négatif.
Elles dépendent de la température à laquelle s’effectue la réaction.
Exemple : la combustion d’une mole de butane \(\left( \ce{C_4H_{10\ (g)}} \right)\) fournit au milieu extérieur une énergie de \(2,9\cdot{10}^6\ \mathrm{J}\).
Exemple : Exemples d'enthalpies de combustion
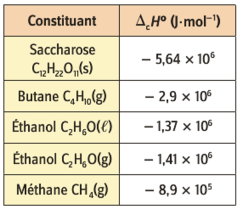
Exemples d'enthalpies de combustion à \(25\ \mathrm{^\circ C}\) sous la pression de de \(1\ \mathrm{bar}\). L'état physique du constituant doit être précisé (solide, liquide, gaz).
Méthode : Calcul d’une enthalpie de combustion
Voir la fiche méthode n°5 en lien ici-même, ou bien dans la section dédiée sur le domaine canoprof : https://p-berger.canoprof.fr/eleve/Commun/Fiches-Méthodes-PDF
🔥 Détermination expérimentale d’une enthalpie de combustion⚓
⚗️ Dispositif expérimental⚓
Bougie chauffe-plat
Sonde thermométrique
Balance de précision
Canette avec dispositif d'isolation thermique

🧪 Mode opératoire⚓
Lire puis mettre en oeuvre le mode opératoire suivant.
Méthode :
Relever la température de la salle de TP.
Peser la canette vide. On note \(m_\text{alu}\) sa masse.
Peser une masse d'eau distillée \(m_\text{eau}=75\ \mathrm{g}\) de température \(\theta_1\) et la verser dans la canette. Noter la valeur précise de la température \(\theta_1\) de l’eau.
Peser la bougie avant de l’allumer. On note \(m_\text{av}\) sa masse.
Chauffer la canette à l'aide du dispositif de chauffage, agiter constamment l'eau dans la canette à l'aide de l'agitateur en verre et noter régulièrement la température de l'eau.
Arrêter le chauffage lorsque la température de l'eau a augmenté d'au moins \(10\ \mathrm{^\circ C}\). Noter la valeur précise de la température finale \(\theta_2\).
Peser à nouveau la bougie. On note \(m_\text{ap}\) sa masse.
📝 Résultats obtenus⚓
Question⚓
Compléter ce qui suit avec vos mesures.
\(m_{alu}=\)
\(m_{av}=\)
\(m_{ap}=\)
\(\theta_1=\)
\(\theta_2=\)
\(m_{eau}=\)
✍🏻 Exploitation des mesures⚓
On suppose que la bougie est constituée de paraffine de formule brute \(\ce{C_{25}H_{52}}\) (en fait un mélange d'hydrocarbures).
Complément : Données
Masse molaire de la paraffine : \(M=352\ \mathrm{g.mol^{-1}}\)
Constituant | Enthalpie de formation \(\Delta_fH^0\ \ \left(\mathrm{J.mol^{-1}}\right)\) |
|---|---|
\(\ce{ O_{2\ ( g ) } }\) | \(0\) |
\(\ce{H_2O_{\ (g) } }\) | \(-2,42\ \times\ {10}^5\) |
\(\ce{CO_{2\ (g)}}\) | \(-3,93\ \times\ {10}^5\) |
\(\ce{C_{25}H_{52\ (g)}}\) | \(-86\ \times\ {10}^5\) |
Définition : 📌 Variation d’énergie lors d’un transfert thermique
Lors d’une variation de température \(\Delta\theta\) d’un corps de masse \(m\), l’énergie \(Q\) du transfert thermique s’exprime par :
La valeur du transfert thermique est positive si le corps reçoit de la chaleur et négative s’il en donne.
Attention : ⚠️
Les valeurs calculées ci-dessous le sont à partir de mes valeurs expérimentales et donc données à titre indicatif. Vous n'aurez certainement pas les mêmes valeurs avec vos mesures.
Il vous faudra donc faire ces calculs avec vos propres mesures expérimentale.
Question⚓
Q4. Calculer l'énergie thermique \(Q_\text{eau}\) reçue par l'eau au cours de la réaction de combustion, sachant que la capacité thermique massique de l'eau vaut \(c_\text{eau}=4,18\ \mathrm{J\cdot g^{-1}\cdot K^{-1}}\).
Solution⚓
Q4.
Le transfert thermique reçu par l’eau au cours de la réaction de combustion est :
\(Q_\text{eau}=m_\text{eau}\times c_\text{eau}\left(\theta_2-\theta_1\right)\)
\(Q_\text{eau}=73,2\times4,18\times\left(40,5-20,5\right)\)
\({\color{blue}Q_\text{eau}=6,12\times{10}^3\ \mathrm{J}}=6,12\ \mathrm{kJ}\)
Question⚓
Q5. Calculer l’énergie thermique \(Q_\text{alu}\) reçue par la canette au cours de la réaction de combustion, sachant que la capacité thermique massique de l’aluminium vaut \(c_\text{alu}=0,890\ \mathrm{J\cdot g^{-1}\cdot K^{-1}}\).
Question⚓
Q6. À l'aide des masses \(m_\text{av}\) et \(m_v{ap}\), déterminer la perte de quantité de matière en paraffine.
Solution⚓
Q6.
\(m_\text{av}=8,8\ \mathrm{g}\) et \(m_\text{ap}=8,4\ \mathrm{g}\) soit une variation de masse \(m_\text{perdue}=m_\text{av}-m_\text{ap}=8,8-8,4=0,4\ \mathrm{g}\)
Ce qui correspond à une variation de quantité de matière :
\(n_\text{perdue}=\dfrac{m_\text{perdue}}{M}=\dfrac{0,4}{352}=1,14\cdot{10}^{-3}\ \mathrm{mol}\)
Question⚓
Q8. En faisant l’hypothèse que l'énergie libérée par la combustion de la paraffine est entièrement utilisée par le chauffage de l'eau et du métal constituant la canette, déduire des résultats précédents l’enthalpie de combustion de la paraffine.
Solution⚓
Q8.
On a déterminé précédemment l’énergie reçue par l’eau et celle reçue par la canette, donc l’énergie libérée par la combustion d’une masse de \(0,3\ \mathrm{g}\) de paraffine, est \(-\left(Q_\text{eau}+Q_\text{alu}\right)\). On peut donc déterminer l’enthalpie de combustion de la paraffine par la relation :
\(\Delta_cH^0\left(\ce{C_{25}H_{52}},\ g\right)=\dfrac{-\left(Q_\text{eau}+Q_\text{alu}\right)}{n_\text{perdue}}\)
\(\Delta_cH^0\left(C_{25}H_{52},g\right)=\dfrac{-\left(6,12\cdot{10}^3+1,55\cdot{10}^2\right)}{1,14\cdot{10}^{-3}}\)
\(\Delta_cH^0\left(C_{25}H_{52},g\right)=-5,50\cdot{10}^6\ \mathrm{J\cdot mol^{-1}}\)
Question⚓
Q10. À l'aide des enthalpies de formation, vérifier la valeur trouvée et commenter.
Utiliser la fiche méthode n°5 : « Calculer l'énergie lors d'une combustion » dont le lien a été donné dans la première partie : « 🔖 Qu'est-ce que l'enthalpie de combustion ? »
Solution⚓
Q10.
Pour écrire la formule de l'enthalpie de combustion, on utilise l'équation de la réaction de combustion trouvée en Q2 :
Calcul de l'enthalpie de combustion à partir des enthalpies de formation :
\(\mathrm{\Delta}_cH^0\left(\ce{C25H52},\ g\right)={\color{blue}25\times\mathrm{\Delta}_fH^0\left(\ce{CO_2},\ g\right)}+{\color{red}26\times\mathrm{\Delta}_fH^0\left(\ce{H_2O},\ g\right)}-{\definecolor{vertRGB}{RGB}{0, 176, 80}\color{vertRGB}\mathrm{\Delta}_fH^0\left(\ce{C25H52},\ g \right)}-{\definecolor{deepcarrotorange}{rgb}{0.91, 0.41, 0.17}\color{deepcarrotorange}38\times\mathrm{\Delta}_fH^0\left(\ce{O_2},\ g\right)}\)
\(\mathrm{\Delta}_cH^0\left(C_{25}H_{52},g\right)={\color{blue}25\times\left(-3,93\cdot{10}^5\right)}+{\color{red}26\times\left(-2,42\cdot{10}^5\right)}-{\definecolor{vertRGB}{RGB}{0, 176, 80}\color{vertRGB}\left(-86\cdot{10}^5\right)}-{\definecolor{deepcarrotorange}{rgb}{0.91, 0.41, 0.17}\color{deepcarrotorange}38\times0}\)
\(\definecolor{fashionfuchsia}{rgb}{0.96, 0.0, 0.63}\color{fashionfuchsia}\mathrm{\Delta}_cH^0\left(C_{25}H_{52},g\right)=-7,5\cdot{10}^6\ \mathrm{J\cdot mol^{-1}}\)
On compare ce résultat à celui de la question Q7. : ce qui fait, avec mes valeurs, un écart relatif d’environ \(27\ \%\).
Question⚓
Q11. Justifier la différence entre cette valeur est celle obtenue expérimentalement. (Ne pas oublier de parler de la chaleur latente de fusion de la paraffine, qui en plus des pertes thermiques intervient pour une part non négligeable dans cet écart).
Solution⚓
Q11.
L’énergie libérée par la combustion ne va pas entièrement dans l’élévation de la température de l’eau et de la canette car l’air entourant la canette est lui aussi chauffé.
De plus, dans le calcul précédent, on a considéré la paraffine sous l’état gazeux, or elle est d’abord solide. Il faut donc ajouter l’énergie nécessaire pour faire passer la paraffine de l’état solide à l’état liquide, puis à l’état gazeux.
Question⚓
Q12. Quelles améliorations du montage peut imaginer pour essayer d’améliorer la concordance entre ce résultat expérimental et la valeur théorique que l’on vient de calculer ?