👨🎓 Les ions oxonium et le pH⚓
Complément : Document n°1 : L'ion oxonium et le potentiel hydrogène
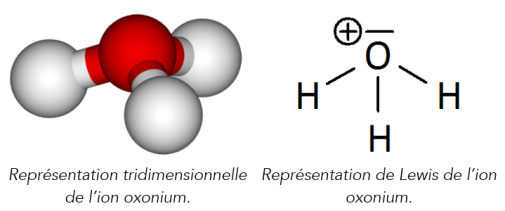
Toute solution aqueuse contient des ions oxonium \(H_3O_{\left( aq \right)}^+\) (parfois encore appelés hydronium). La concentration de ces ions joue un rôle majeur dans le déroulement d'un très grand nombre de réactions chimiques.
Les ions oxonium peuvent par exemple provenir de l'action d'un ion \(H^+\) sur l'eau :
\(H_{\left( aq \right)}^++H_2O_{\left( \ell \right)}\rightarrow H_3O_{\left( aq \right)}^+\)
Complément : Document n°2 : Le potentiel hydrogène
La valeur de la concentration molaire \(\Big[H_3O^+\Big]\) pouvant varier de quelques \(\mathrm{mol.L^{-1}}\) à \({10}^{-14}\ \mathrm{mol.L^{-1}}\), le chimiste danois S. Sørensen proposa en 1909 une grandeur plus facile à manipuler : le potentiel hydrogène ou pH.
Le pH est une grandeur sans unité qui quantifie l'acidité d'une solution aqueuse et est défini par la relation suivante :
Cette relation est valable pour \(\Big[H_3O^+\Big]<0,10\ \mathrm{mol.L^{-1}}\).
La mesure du pH permet de calculer la concentration molaire en ions oxonium, grâce à la relation suivante :

Remarque :
La concentration en ions oxonium obtenue par la relation précédente est donnée avec deux chiffres significatifs lorsque le pH est donné avec un chiffre après la virgule. Cette règle reste valable si le pH est supérieur à 10 et donné avec trois chiffres significatifs.
Complément : Document n°3 : Point mathématiques sur les log
\(\large \log\ {\Big(A\times B\Big)}=\log{\ A}+\log{\ B}\)
\(\large \log\ {\Big( 10^a\Big)}=a\)
\(\large \log \ {\Big(\ \dfrac{\ A\ } {B}\ \Big)}=\log{\ A}-\log{\ B}\)
\(\large 10^{\log \ a }=a\)
Question⚓
Q2. Calculer les pH correspondant à des concentrations en oxonium de :
\(\large \color{black} {\Big[H_3O^+\Big]=0,050\ \mathrm{mol.L^{-1}} }\)
\(\large \color{black} {\Big[H_3O^+\Big]=10^{-7}\ \mathrm{mol.L^{-1}} }\)
\(\large \color{black} {\Big[H_3O^+\Big]=10^{-14}\ \mathrm{mol.L^{-1}} }\)
(Aide : utiliser une formule du Doc.2)
Question⚓
Q3. Justifier alors la phrase du Doc.1.2 : « ...le chimiste danois S. Sørensen proposa en 1909 une grandeur plus facile à manipuler : le potentiel hydrogène ou pH. »
.
Question⚓
Q4. Quelle est l'évolution de la valeur du pH lorsque la concentration en ion oxonium est multipliée par 10 ?
Solution⚓
A1-Q4.
Soit \(\mathrm{pH}_1=-\log{\ \Big[H_3O^+\Big]}\).
\(\mathrm{pH}_2=-\log{\ \left(10\times\Big[H_3O^+\Big]\ \right)}\)
\(\mathrm{pH}_2=-\log{10}\ - \ \log{\ \Big[H_3O^+\Big]}\)
\(\mathrm{pH}_2=-1+\mathrm{pH}_1\)
\(\color{blue} {\mathrm{pH}_2=\mathrm{pH}_1-1}\)
Lorsque la concentration est multipliée par 10, le \(\mathbf{pH}\) diminue de 1.
💪 Exercice n°1 : Calculs autour du pH⚓
On dissout \(n=7,0\cdot{10}^{-3}\ \mathrm{mol}\) de chlorure d'hydrogène \(H{C\ell}_{\left(g\right)}\) dans un volume \(V=0,35\ \mathrm{L}\) d'eau.
Il se produit alors la réaction acido-basique suivante : \(H{C\ell}_{\left(g\right)}+H_2O_{\left(\ell\right)}\longrightarrow H_3O_{\left(aq\right)}^++C\ell_{\left(aq\right)}^-\).
Question⚓
Q5. Calculer le pH de cette solution.
Solution⚓
A1-Q5.
Lorsqu'il disparait \(n\ \mathrm{mol}\) de \(H{C\ell}_{\left(g\right)}\), il se forme \(n_{H_3O^+}=n\ \mathrm{mol}\) d'ions \(H_3O_{\left(aq\right)}^+\).
\(\mathrm{pH}=-\log{\ \Big[H_3O^+\Big]}\)
\(\mathrm{pH}=-\log{\ \left(\ \dfrac{\ n_{H_3O^+} \ }{V}\ \right)}\)
\(\mathrm{pH}=-\log{\ \left(\ \dfrac{\ n\ }{V}\ \right)}\)
\(\mathrm{pH}=-\log{\ \left(\ \dfrac{7,0\cdot{10}^{-3}}{0,35}\ \right)}\)
\(\color{blue} \mathrm{pH}=1,7\)
On dissout \(n=1,5\cdot{10}^{-4}\ \mathrm{mol}\) d'acide sulfurique \(H_2SO_{4\ \left(\ell\right)}\) dans un volume \(V=100\ \mathrm{mL}\) d'eau.
Il se produit alors la réaction acido-basique suivante : \( H_2SO_{4\ \left(\ell\right)}+2\ H_2O_{\left(\ell\right)}\longrightarrow2\ H_3O_{\left(aq\right)}^++SO_{4\ \left(aq\right)}^{2-}\).
Question⚓
Q6. Calculer le pH de cette solution.
Solution⚓
A1-Q6.
Lorsqu'il disparait \(n\ \mathrm{mol}\) de \(H_2SO_{4\ \left(\ell\right)}\), il se forme \(n_{H_3O^+}=2\ n\ \mathrm{mol}\) d'ions \(H_3O_{\left(aq\right)}^+\).
\(\mathrm{pH}=-\log{\ \Big[H_3O^+\Big]}\)
\(\mathrm{pH}=-\log{\ \left(\ \dfrac{\ n_{H_3O^+} \ }{V}\ \right)}\)
\(\mathrm{pH}=-\log{\ \left(\ \dfrac{\ 2\ n\ }{V}\ \right)}\)
\(\mathrm{pH}=-\log{\ \left(\ \dfrac{ 2\times1,5\cdot{10}^{-4} } { 100\cdot{10}^{-3} } \ \right)}\)
\(\color{blue} \mathrm{pH}=2,5\)
Question⚓
Q7. Un jus de citron possède un \(\mathrm{pH}=2,4\). Calculer la concentration en ion oxonium \(\Big[H_3O^+\Big]\) dans cette solution.
👨🎓 La mesure du pH⚓
Complément : Document n°4 : Comment mesurer le pH ?
💪 Exercice n°2 : pH et incertitude⚓
L'incertitude sur la mesure d'un pH au pH-mètre est au mieux de l'ordre de 0,05 unité. On considère une solution pour laquelle un pH-mètre indique \(\mathrm{pH}=5,30\).
Question⚓
Q10. Écrire, avec 2 chiffres significatifs, la valeur de la concentration des ions oxonium avec son incertitude \(U\left(\ \Big[H_3O^+\Big]\ \right)\).
L'incertitude sur la valeur V est l'encadrement de la valeur \(V\) mesurée avec le signe \(\large \pm\), elle est notée \(\large U\left(V\right)\). Le résultat s'écrit alors : \(\large V \pm U\left(V\right)\).
