📄 Documents⚓
📄 Document n°1 : Octaves et bandes⚓
Complément : 1️⃣ Spectre par fréquence
Un son est caractérisé par un niveau sonore pour chaque fréquence. Pour étudier un bruit, il est nécessaire d’analyser l’ensemble du spectre (\(20\ \mathrm{Hz}\) à \(20\ 000\ \mathrm{Hz}\) pour l’oreille humaine).
Exemple de spectre d’un ventilateur par fréquence (extrait jusqu’à 4664Hz) :
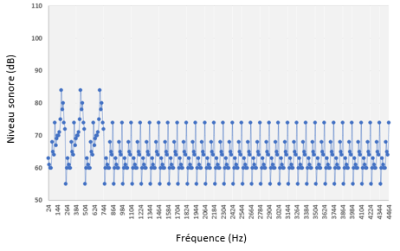
Complément : 2️⃣ Spectre par bande d’octave
L’analyse spectrale par fréquence est trop fine et ne permet pas une lecture efficace. Et comme les fréquences audibles par l'homme représentent une gamme très importante de \(20\ \mathrm{Hz}\) jusqu'à \(20\ 000\ \mathrm{Hz}\), afin de simplifier l’analyse, le spectre est découpé en bandes de fréquences appelées des octaves.
Le principe étant d’obtenir des bandes de largeur relative constante \(\frac{\Delta f}{f}\) correspondant au processus de l’audition humaine. Une octave correspond au doublement de la fréquence.
L'octave est une bande de fréquence centrée à la fréquence \(f\) dont la fréquence minimale est \(f_1\) est la fréquence maximale est \(f_2\) telle que : \(f_1=\dfrac{f}{\sqrt{2}}\) et \(f=\dfrac{f_2}{\sqrt{2}}\).
Les bandes d'octaves utilisées dans le bâtiment sont :
\(63\ \mathrm{Hz}\) | \(125\ \mathrm{Hz}\) | \(250\ \mathrm{Hz}\) | \(500\ \mathrm{Hz}\) | \(1\ 000\ \mathrm{Hz}\) | \(2\ 000\ \mathrm{Hz}\) | \(4\ 000\ \mathrm{Hz}\) | \(8\ 000\ \mathrm{Hz}\) |
Exemple de spectre d’un ventilateur par bande d’octaves :
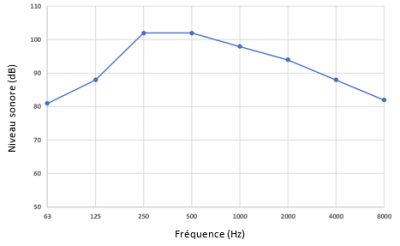
Complément : 3️⃣ Spectre par tiers d’octaves
La tendance forte de notre métier est l’analyse par tiers d’octave qui permet une analyse plus précise du bruit que par bandes d’octaves. A noter que la règlementation demande d’effectuer les tests acoustiques en tiers d’octaves.
Exemple de spectre d’un ventilateur par tiers d’octaves :
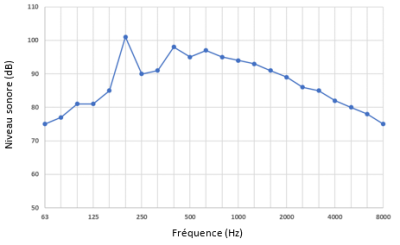
Complément : 4️⃣ Calcul d’un niveau global
À partir de ce découpage en bande de fréquences par octave (ou tiers d’octave), le niveau global peut être calculé en appliquant la formule suivante :
\(\Large L_\text{global}=10\ \log { \left( 10^{\frac{L_{63} }{10} } + 10^{\frac{L_{125} }{10} } + 10^{\frac{L_{250} }{10} } +10^{\frac{L_{500} }{10} } +10^{\frac{L_{1000} }{10} } + ... \right)}\)
Exemple :
Deux équipements peuvent avoir des spectres acoustiques différents mais un niveau global identiques.
Exemple de deux centrales de traitement d’air :
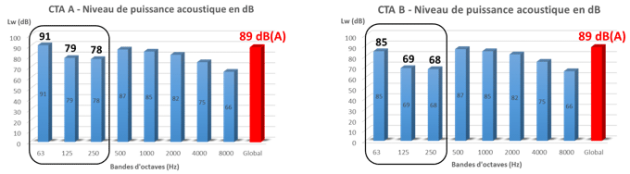
Nota : il est d’usage de présenter la puissance acoustique d’un équipement par bande d’octave en dB et le niveau global en dB(A).
ATTENTION : pour déterminer le traitement acoustique optimal, il est indispensable d’avoir le spectre acoustique de l’équipement en bande d’octaves (ou tiers d’octaves).
📄 Document n°2 : Pondération du niveau sonore⚓
Complément : 📄 Document n°2 : Pondération du niveau sonore
Les courbes d'égales sensations sonores (dites de Fletcher et Munson) donnent le niveau de la sensation sonore en fonction du niveau réel du son, exprimé en décibel (dB).
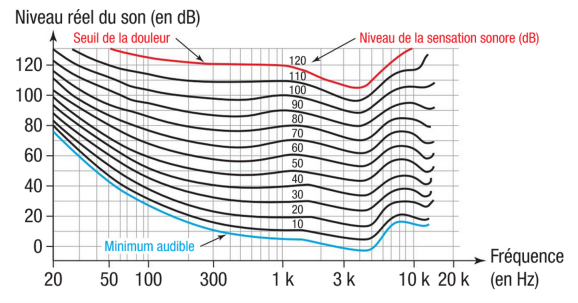
À la différence d'un sonomètre, l'oreille humaine n'a pas la même sensibilité pour toutes les fréquences.
Afin d'obtenir un niveau sonore proche de celui perçu par l'oreille humaine, une pondération « physiologique » a été introduite en se basant sur les courbes isophonique (courbe d'égale sensibilité), il s'agit de la pondération A.
La pondération ‘A’ a été conçue pour se rapprocher de la réaction de l’oreille humaine au bruit. L’oreille humaine n’est pas très sensible aux basses et hautes fréquences, mais entre 500 Hz et 6 kHz l’oreille est alors beaucoup plus sensible.
Un niveau sonore pondéré est exprimé en dB(A).
Le filtre de pondération ‘A’ couvre la gamme entière des fréquences de 20 Hz à 20 kHz, mais sa façon de percevoir le son se rapproche de la sensibilité de fréquence de l’oreille humaine. Ainsi, la valeur pondérée ‘A’ d’une source sonore est une approximation de la façon dont l’oreille humaine perçoit le bruit.
Le filtre de pondération (A) permet de corriger les bruits dont les niveaux sonores sont inférieurs à \(55\ \mathrm{dB}\).
Sur les bandes d'octaves, la pondération A introduit les corrections suivantes :
Fréquence en \(\mathrm{Hz}\) | \(63\ \mathrm{Hz}\) | \(125\ \mathrm{Hz}\) | \(250\ \mathrm{Hz}\) | \(500\ \mathrm{Hz}\) | \(1\ 000\ \mathrm{Hz}\) | \(2\ 000\ \mathrm{Hz}\) | \(4\ 000\ \mathrm{Hz}\) | \(8\ 000\ \mathrm{Hz}\) |
Correction en \(\mathrm{dB}\) | \(-26,2\) | \(-16,1\) | \(-8,6\) | \(-3,2\) | \(0\) | \(+1,2\) | \(+1\) | \(-1,1\) |
❓ Avez-vous compris les documents ?⚓
💪 Exercice⚓
On considère le spectre d’octave d’un bruit routier.
Fréquence En Hz | 63 Hz | 125 Hz | 250 Hz | 500 Hz | 1 000 Hz | 2 000 Hz | 4 000 Hz | 8 000Hz |
Niveau L en dB | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 |
Question⚓
Q4. Calculer le niveau d’intensité sonore global.
Solution⚓
Q4.
\(\Large L_\text{global}=10\ \log { \left( 10^{\frac{L_{63} }{10} } + 10^{\frac{L_{125} }{10} } + 10^{\frac{L_{250} }{10} } +10^{\frac{L_{500} }{10} } +10^{\frac{L_{1000} }{10} } + ... +10^{\frac{L_{8000} }{10} }\right)}\)
\(\Large L_\text{global}=10\ \log { \left( 10^{ \frac{80}{10} } + 10^{ \frac{80}{10} } + 10^{ \frac{80}{10} } + 10^{ \frac{80}{10} } + ... + 10^{ \frac{80}{10} }\right)}\)
\(\Large L_\text{global}=10\ \log { \left( 8 \times 10^{ \frac{80}{10} }\right)}\)
\(\Large L_\text{global}=89\ \mathrm{dB}\)
Question⚓
Q5. Appliquer les pondérations A.
Question⚓
Q6. Calculer le niveau d’intensité sonore global en dB(A). Commentez.
Solution⚓
Q6.
\(\Large L_\text{global}=10\ \log { \left( 10^{\frac{L_{63} }{10} } + 10^{\frac{L_{125} }{10} } + 10^{\frac{L_{250} }{10} } +10^{\frac{L_{500} }{10} } +10^{\frac{L_{1000} }{10} } + ... +10^{\frac{L_{8000} }{10} }\right)}\)
\(\Large L_\text{global}=10\ \log { \left( 10^{ \frac{53,8}{10} } + 10^{ \frac{63,9}{10} } + 10^{ \frac{71,4}{10} } + 10^{ \frac{76,8}{10} } + 10^{ \frac{80}{10} } + 10^{ \frac{81,2}{10} }+ 10^{ \frac{81}{10} } + 10^{ \frac{78,9}{10} }\right)}\)
\(\Large L_\text{global}=87\ \mathrm{dB}\)
Le niveau d'intensité sonore global en dB(A) est 2 dB plus faible que le niveau d'intensité sonore globale en dB. Le bruit parait presque 2x moins bruyant avec la pondération que sans.