🚩 Définitions⚓
Définition : Document n°1 - Transferts thermique et température - 📌 À SAVOIR 📌
Entre deux corps dont la température est différente se produit inévitablement un transfert thermique : la chaleur (énergie thermique, notée \(Q\)) se déplace du corps chaud vers le corps froid jusqu'à l’équilibre des températures. Ce transfert est irréversible.
Il s’agit du 1er principe de la thermodynamique.
Autrement dit, lorsqu’un corps chaud est en présence d’un corps froid, le corps froid voit sa température augmenter, et non le contraire : la température du corps froid ne baisse pas et celle du corps chaud n’augmente pas.
Le corps le plus chaud va céder de l'énergie sous forme de chaleur au corps le plus froid
Définition : Document n°2 - Le flux thermique Φ - 📌 À SAVOIR 📌
Le transfert thermique peut être plus ou moins rapide. Le flux thermique noté \(\mathbf \Phi\) traduit la vitesse de ce transfert et correspond à l’énergie thermique \(\mathbf Q\) transférée pendant une durée \(\mathbf{ \Delta t}\) :
La relation liant \(\mathbf \Phi\), \(\mathbf Q\) et \(\mathbf{ \Delta t}\) et les unités correspondantes sont :
Remarque :
Le flux thermique ayant la dimension d’une puissance, on parle aussi de puissance thermique.
Une habitation bien isolée possède un faible flux thermique et donc des transferts thermiques avec l’extérieur lents.
Exemple :
Dire qu’une paroi est traversée par un flux thermique de \(1\ 500\ \mathrm{W}\) veut dire que la paroi laisse passer 1 500 Joules à chaque seconde.
Question⚓
Q1. Compléter la définition précédente en donnant la relation liant \(\mathbf \Phi\), \(\mathbf Q\) et \(\mathbf{ \Delta t}\) ainsi que les unités correspondantes.
Solution⚓
Q1.
\(\mathbf Q\) : Énergie thermique transférée en joules \(\mathbf J\)
\(\mathbf {\Delta t}\) : Durée du transfert en secondes \(\mathbf s\)
\(\mathbf \Phi\) : Flux thermique transférée en watt \(\mathbf W\)
Question⚓
Une habitation perd thermiquement \(5\ 000\ 000\ \mathrm{J}\) par heure.
Q2. Calculer la valeur du flux \(\mathbf{\Phi}\) correspondant aux pertes. En déduire la puissance thermique qu’il faudra fournir pour compenser les pertes ainsi que le nombre de radiateurs correspondants sachant que chacun possède une puissance de \(1\ 000\ \mathrm{W}\).
Solution⚓
Q2.
On a \(Q=5\ 000\ 000\ \mathrm{J}\) et \(\Delta t = 1\ \mathrm{h}=3\ 600\ \mathrm{s}\).
Donc le flux thermique perdu est : \(\Phi=\dfrac{5\ 000\ 000}{3\ 600}=1,389\cdot 10^3\ \mathrm{W}\).
Il faut donc fournir une puissance thermique \(P=1,389\cdot 10^3\ \mathrm{W}\) afin de compenser ces pertes thermiques.
Il faudra donc le nombre de radiateurs suivant : \(\dfrac{1,389\cdot 10^3}{1\ 000}=1,4\) soit \(\approx 2\) radiateurs de \(1\ 000\ \mathrm{W}\).
Définition : Document n°3 - La densité de flux thermique - 📌 À SAVOIR 📌
Le flux thermique étant échangé au travers d’une surface \(\mathbf S\), on définit la densité de flux thermique\( \mathbf{\varphi}\) qui s’exprime en \(\mathbf{W.m^{-2}}\).
La relation liant \(\mathbf \Phi\), \(\mathbf{\varphi}\) et \(\mathbf S\) et les unités correspondantes sont :
Remarque :
Un grand flux thermique peut traverser une grande surface, au final sa densité de flux sera relative. Inversement, un petit flux peut traverser une petite surface et posséder une densité de flux supérieure à la précédente… (à méditer).
Question⚓
Q3. Compléter la définition précédente en donnant la relation liant \(\mathbf \Phi\), \(\mathbf{\varphi}\) et \(\mathbf S\) ainsi que les unités correspondantes.
Solution⚓
Q3.
\(\mathbf \Phi\) : Flux thermique transférée en \(\mathbf W\)
\(\mathbf {S}\) : Surface en \(\mathbf {m^2}\)
\(\mathbf \varphi\) : Densité de flux thermique en \(\mathbf{W.m^{-2}}\)
👨🎓 LES MODES DE TRANSFERTS THERMIQUES⚓
Complément : Document n°4 - Les 3 modes de transferts thermiques
La conduction :
Elle a lieu essentiellement dans les solides mais peut aussi se rencontrer, à une échelle beaucoup plus faible, dans les fluides. C'est un transfert thermique par contact sans transport de matière. D'un point de vue microscopique, les constituants du matériau communiquent à leurs voisins leur agitation thermique, tout en restant globale¬ment à la même place.
La convection :
Elle a lieu dans un fluide dont la température n'est pas homogène : la zone chaude, moins dense que la zone froide s'élève.
La convection est donc un transfert thermique porté par un mouvement de matière.
Le rayonnement :
Tout corps, en raison de sa température, émet des rayonnements thermiques. Le rayonnement est un transfert thermique qui ne nécessite pas de milieu matériel, les ondes électromagnétiques se déplaçant dans le vide.
💪 Exercice n°1⚓
Question⚓
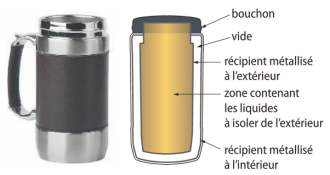
Q5. Voici ci-contre le schéma d'une bouteille thermos. Comment peut-elle, grâce à sa structure, limiter les 3 types de transferts thermiques ?
Solution⚓
A1.Q5. (Ex.4)
Les deux récipients ne sont pas en contact, limitant ainsi le transfert par conduction. Le vide a été fait entre les deux récipients, empêchant ainsi le transfert par convection. Les parois intérieures des deux récipients sont recouvertes de métal afin d'éviter le transfert par rayonnement.
💪 Exercice n°2⚓
🚩 Conclusion⚓
🔥 Les transferts thermiques par conduction⚓
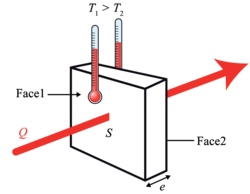
Définition : Document n°5 - Transferts thermiques par conduction (Loi de Fourier) - 📌 À SAVOIR 📌
Dans les solides (mur, etc.), le transfert de chaleur s’effectue par conduction uniquement (de proche en proche).
La densité de flux thermique \(\mathbf \varphi\) transférée par conduction est :
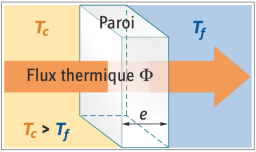
Proportionnelle à la différence de température \(\mathbf {T_\text{c} - T_\text{f}}\) de part et d’autre de la paroi (telle que \(T_\text{c}>T_\text{f}\)) ;
Liée au matériau (à sa capacité à conduire la chaleur). On associe un nombre \(\left(\ \mathbf {\lambda}\ \right)\) à chaque matériau ;
Inversement proportionnelle à l’épaisseur \(\mathbf e\) de la paroi.
La relation liant \(\mathbf \varphi\), \(\mathbf {\Delta T}\), \(\mathbf {\lambda}\) et \(\mathbf e\) est ;
\(\mathbf {\lambda}\) :Conductivité thermique d’un matériau, elle caractérise la manière dont le matériau laisse passer la chaleur, s’exprime en \(\mathbf{W\cdot m^{-1}\cdot K^{-1}}\)
\(\mathbf e\) : l’épaisseur de la paroi, en \(\mathbf m\).
\(\mathbf {T_\text{c} - T_\text{f}}\) : écart de température entre la face la plus chaude \(T_\text{c}\) et la face la plus froide \(T_\text{f}\), en \(\mathbf{^\circ C}\) ou en \(\mathbf{K}\).
Exemple :
Verre : \(\lambda = 1,15\ \mathrm{W\cdot m^{-1}\cdot K^{-1}}\).
Cela veut dire que pour un morceau de verre d’épaisseur \(1\ \mathrm m\), il passe 1,15 Joules chaque seconde, si l’écart de température entre les deux faces vaut \(1\ \mathrm{^\circ C}\) ou \(1\ \mathrm{K}\).
Question⚓
Q8. Compléter la définition précédente en donnant la relation liant \(\mathbf \varphi\), l'écart de température \(\mathbf {T_\text{c} - T_\text{f}}\), \(\mathbf {\lambda}\) et \(\mathbf{e}\).
Complément : Document n°6 - Valeurs de conductivités thermiques
Dans le tableau ci-dessous, sont reportées les conductivités de quelques corps solides, liquides et gazeux. (Ce n'est pas à savoir !)
Matériaux | \(\lambda\; \left( \ W\cdot m^{-1}\cdot K^{-1}\ \right)\) |
|---|---|
Cuivre | \(386\) |
Fer (pur) | \(73\) |
Acier Inoxydable | \(16\) |
Fonte | \(55\) |
Ardoise | \(2,2\) |
Carrelage | \(1,3\) |
Bois | \(0,16\) |
Polystyrène | \(0,038\) |
Matériaux | \(\lambda\; \left( \ W\cdot m^{-1}\cdot K^{-1}\ \right)\) |
|---|---|
Verre | \(0,78\) |
Papier | \(0,48\) |
Chêne | \(0,17\) |
Laine de verre | \(0,038\) |
Eau | \(0,556\) |
Air | \(0,0262\) |
Béton | \(2,2\) |
Enduit plâtre | \(0,57\) |
Complément : Remarque :
Pour garder un plat au chaud plus longtemps, il est préférable de la mettre dans une cocotte en fonte, qui possède un \(\lambda\) plus petit que celui du cuivre dans le cas d’une casserole en cuivre.
Définition : Document n°7 - Résistance thermique d’une paroi - 📌 À SAVOIR 📌
On peut aussi regarder la paroi du point de vue de sa résistance thermique surfacique, et exprimer la densité de flux au regard de l’écart de température, et la résistance totale de la paroi. Ainsi, on peut écrire :
Avec :
\(\mathbf {T_\text{c} - T_\text{f}}\) : écart de température entre la face la plus chaude \(T_\text{c}\) et la face la plus froide \(T_\text{f}\), en \(\mathbf{^\circ C}\) ou en \(\mathbf{K}\).
\(R\) la résistance thermique totale de la paroi, s’exprimant en \(\mathrm{m^2 \cdot K \cdot W^{-1}}\).
En recoupant cette formule et celle de la définition précédente, on trouve la relation suivante :
La résistance thermique \(R\) d'une paroi traduit sa capacité à s'opposer au passage de la chaleur.
Rappel :
Rappel : Une paroi plane, dont les deux faces sont à des températures différentes, est le siège d’un transfert thermique par conduction. Ce transfert se fait spontanément de la source chaude vers la source froide et est naturellement irréversible.
Remarque : Plus \(R\) est grand, plus le matériau est isolant.
Un bon isolant a donc une forte résistance thermique surfacique.
Attention :
Note n°1 :\(\)
\(\dfrac{1}{R}\) homogène à des \(\mathrm{W/m^{2}/K}\) : c.a.d. à une conductance, ou encore au nombre de \(\mathrm W\) qui traverse une paroi identifiée par degré d’écart.
Cette conductance se note généralement \(\mathbf U\).
Il vient : \(\mathbf{U=\dfrac{1}{R}=\dfrac{\lambda}{e}}\)
Note n°2 :
Il est également possible de définir la résistance thermique, notée pour ne pas la confondre \(R_\text{th}\), s’exprimant en \(\mathrm{^\circ C\cdot W^{-1}}\), telle que :
\[\definecolor{grisRGB}{RGB}{225, 225, 225} {\fcolorbox{red}{grisRGB}{$ \begin{array}{rcl} \mathbf{ R_\text{th} = \dfrac{R}{S}} \end{array} $}} \hspace{1cm} \textsf{on a alors : } \hspace{5mm} \mathbf{R_\text{th} = \dfrac{e}{\lambda \times S} }\]Il vient logiquement que :
\[\definecolor{grisRGB}{RGB}{225, 225, 225} \begin{array}{rll} \mathbf{\Phi = S \times \varphi } & & \textsf{donc : } \mathbf{\Phi = S \times \dfrac{T_\text{c} - T_\text{f}}{R} } \\ & & \textsf{on a alors : } {\fcolorbox{red}{grisRGB}{$ \begin{array}{rcl} \mathbf{ \Phi = \dfrac{T_\text{c} - T_\text{f}}{R_\text{th}}} \end{array} $}} \end{array}\]
Complément : Document n°8
Mais quelle est la subtilité entre \(R\) et \(R_\text{th}\) ?
\(R\) donne des informations sur la qualité thermique d’un matériau.
\(R_\text{th}\) s’intéresse plus au global, c’est-à-dire à la résistance thermique global d’un ouvrage compte tenu de ses dimensions.
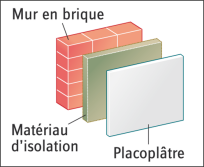
Complément : Document n°9 - Paroi constituée de plusieurs couches de matériaux différents - 📌 À SAVOIR 📌
Lorsqu'un mur est constitué d'une succession de couches de matériaux différents, la résistance thermique se détermine comme ceci :
\(R_\text{total}=R_1+R_2+R_3+...\)
Dans l'exemple ci-contre, on aura : \(R_\text{mur}=R_\text{placo}+R_\text{isolant}+R_\text{brique}\)
💪 Exercices⚓
Question⚓
Q10. Calculer la densité de flux thermique traversant une vitre de \(4,0\ \mathrm{mm}\) d’épaisseur en verre \(\left( \lambda= 0,78\ \mathrm{W\cdot m^{-1} \cdot \mathrm{^\circ C}^{-1} } \right)\), sachant que la température intérieure est de \(20 \mathrm{^\circ C}\) et que la température extérieure vaut \(15 \mathrm{^\circ C}\). (Valeur à trouver : \(\varphi= 9,8\cdot 10^2\ \mathrm{W/m^2}\))
Question⚓
Q12. Que va-t-il se passer pour la densité de flux si \(T_\text{ext}\) diminue ?
Question⚓
Q13. Même chose si \(T_\text{ext} = 30\ \mathrm{^\circ C}\) et \(T_\text{int} = 20\ \mathrm{^\circ C}\) . Commenter. (Valeur à trouver : \(\varphi= 2,0\cdot 10^3\ \mathrm{W/m^2}\))
Solution⚓
Q13.
\(\varphi = \dfrac{\lambda \times \left( T_\text{c} - T_\text{f} \right)}{e}\)
\(\varphi = \dfrac{0,78 \times \left( 30 -20 \right)}{4,0\cdot 10^{-3}}\)
\(\varphi = 2,0\cdot 10^3\ \mathrm{W\cdot m^{-2}}\)
La valeur de la densité de flux est doublée par rapport à la valeur précédemment calculée, ce qui est normal puisque l'écart de température est doublé.
Question⚓
Q14. Même question que « Q10. », mais la vitre fait \(8,0\ \mathrm{mm}\) d’épaisseur. Commenter. (Valeur à trouver : \(\varphi= 4,9\cdot 10^2\ \mathrm{W/m^2}\))
Question⚓
Q15. Même chose que « Q1. », mais la vitre de \(4,0\ \mathrm{mm}\) d’épaisseur est en Altuglas \(\left( \lambda_\text{altuglass}= 0,17\ \mathrm{W\cdot m^{-1} \cdot \mathrm{^\circ C}^{-1} } \right)\). Commenter. (Valeur à trouver : \(\varphi= 2,1\cdot 10^2\ \mathrm{W/m^2}\))
Question⚓
Q17. Calculer la résistance thermique surfacique \(R\) d’une vitre en double vitrage (paroi multicouche), composée de 2 parois en verre de \(4,0\ \mathrm{mm}\) d’épaisseur, séparées d’une épaisseur d’air de \(16,0\ \mathrm{mm}\) . Préciser la méthode en une phrase.
Solution⚓
Q17.
\(R=\dfrac{e_\text{verre} }{\lambda_\text{verre}}+\dfrac{e_\text{air} }{\lambda_\text{air}}+\dfrac{e_\text{verre} }{\lambda_\text{verre}}=2\times \dfrac{e_\text{verre} }{\lambda_\text{verre}}+\dfrac{e_\text{air} }{\lambda_\text{air}}\)
\(R=2\times \dfrac{4,0\cdot 10^{-3}}{0,78}+\dfrac{16,0\cdot 10^{-3} }{0,026}\)
\(R=6,3\cdot 10^{-1}\ \mathrm{m^2 \cdot K \cdot W^{-1}}\)
Il faut ajouter les résistances thermiques des 3 couches composant le double-vitrage : le verre + l'air + le verre.
Question⚓
Q19. Déterminer l’épaisseur d’un béton de conductivité thermique \(\lambda_\text{béton} =1,6\ \mathrm{W\cdot m^{-1} \cdot K^{-1}}\), qui aurait la même résistance thermique \(R_p\) qu’un polystyrène, de conductivité thermique \(\lambda_\text{polyst.} =0,04\ \mathrm{W\cdot m^{-1} \cdot K^{-1}}\), et de \(5,0 \ \mathrm{cm}\) d’épaisseur. (réponse : \(e =2 \ \mathrm{m}\))
Commenter.
Solution⚓
Q19.
On veut \(R_\text{béton}=R_\text{polyst.}\) c'est-à-dire :
\(\dfrac{e_\text{béton}}{\lambda_\text{béton}}=\dfrac{e_\text{polyst.}}{\lambda_\text{polyst.}}\)
\(e_\text{béton}=\dfrac{\lambda_\text{béton} \times e_\text{polyst.}}{\lambda_\text{polyst.}}\)
\(e_\text{béton}=\dfrac{1,6 \times 5,0}{0,04}=2\ \mathrm{m}\)
Le polystyrène fait un bien meilleur isolant que le béton car il faut 2 m de béton pour être équivalant à 5 cm de polystyrène.
Question⚓
Q20. Quel est, de la plaque de verre de \(12,0 \ \mathrm{mm}\) ou de la plaque d'Altuglas® de \(4,0 \ \mathrm{mm}\), le meilleur isolant thermique ?
Solution⚓
Q20.
On a vu en Q15 que \(\lambda_\text{altuglass}= 0,17\ \mathrm{W\cdot m^{-1} \cdot \mathrm{^\circ C}^{-1} }\) et en Q10 que \(\lambda_\text{verre}= 0,78\ \mathrm{W\cdot m^{-1} \cdot \mathrm{^\circ C}^{-1} }\).
Comparons leur résistance thermique :
\(R_\text{verre}=\dfrac{e_\text{verre}}{\lambda_\text{verre}}=\dfrac{12,0 \cdot 10^{-3} } {0,78}=1,5\cdot \cdot 10^{-2}\ \mathrm{m^{2} \cdot \mathrm{^\circ C} \cdot W^{-1} }\)
\(R_\text{altuglass}=\dfrac{e_\text{altuglass}}{\lambda_\text{altuglass}}=\dfrac{4,0 \cdot 10^{-3} } {0,17}=2,4\cdot \cdot 10^{-2}\ \mathrm{m^{2} \cdot \mathrm{^\circ C} \cdot W^{-1} }\)
On obtient que \(R_\text{verre} < R_\text{altuglass}\) ce qui prouve que la plauqe d'altuglass est un bien meilleur isolant que la plaque de verre.
Question⚓
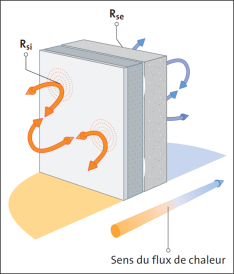
Dans la réalité, il est nécessaire d’ajouter à la résistance thermique surfacique totale d’une paroi 2 termes supplémentaires, appelés respectivement résistance thermique superficielle interne et résistance superficielle externe, notées respectivement \(r_\text{si}\) (ou \(R_\text{SI}\) ou encore \(r_\text{i}\)) et \(r_\text{se}\) (ou \(R_\text{SE}\) ou encore \(r_\text{e}\)) . \(r_\text{s1}\) et \(r_\text{se}\) ont des valeurs variables en fonction de l’orientation des parois, notamment, mais leurs valeurs se situent aux alentours de \(0,1\ \mathrm{m^2 \cdot \mathrm{^\circ C} \cdot W^{-1}}\).
Q21. Quelle est l’origine de \(r_\text{s1}\) et \(r_\text{se}\) ?
Définition : À retenir
\(r_\text{si}\) et \(r_\text{se}\) valent environ \(0,1\ \mathrm{m^2 \cdot \mathrm{^\circ C} \cdot W^{-1}}\).
☕ Les transferts thermiques par convection (Loi de Newton)⚓
Définition : Loi de Newton (1701)
Lorsqu’une paroi échange de la chaleur par convection avec l’extérieur, la densité de flux \(\Large \mathbf{\varphi}\) qu’elle échange est proportionnelle à la différence de température \(\mathbf{T_\text{c} - T_\text{f}}\) entre la paroi et le milieu fluide extérieur.
Le coefficient de proportionnalité se nomme coefficient d’échange thermique de surface \(\mathbf{h}\) et s’exprime en \(\mathbf{ W \cdot m^{-2}\cdot K^{-1}}\).
L'équation modélisant ce phénomène est :
Ce coefficient d’échange \(\mathbf{h}\) tient compte des différentes propriétés physiques et cinématiques du fluide léchant la paroi.
Question⚓
Q22. Compléter la définition précédent en donnant l’équation modélisant ce phénomène. Préciser les unités associées.
Solution⚓
Q22.
\(\varphi\) : densité de flux
\(h\) : Coefficient d'échange thermique de surface en
\(\mathbf {T_\text{c} - T_\text{f}}\) : écart de température entre la face la plus chaude \(T_\text{c}\) et la face la plus froide \(T_\text{f}\), en \(\mathbf{^\circ C}\) ou en \(\mathbf{K}\).
Définition : La résistance thermique d’échange superficielle (Rsi et Rse) et coefficient d’échange thermique superficiel (hi et he)
La résistance thermique d’échange d’une surface intérieure \(R_\text{si}\) est égale à l’inverse du coefficient d’échange thermique de surface intérieure \(h_\text{i}\). De même pour la résistance thermique d’échange d’une surface extérieure \(R_\text{se}\) avec le coefficient d’échange thermique de surface extérieur \(h_\text{e}\).
Avec :
\(R_\text{si}\) : résistance thermique d’échange d’une surface intérieure \(\mathrm{m^{2} \cdot \mathrm{^\circ C} \cdot W^{-1} }\)
\(R_\text{se}\) : résistance thermique d’échange d’une surface extérieure \(\mathrm{m^{2} \cdot \mathrm{^\circ C} \cdot W^{-1} }\)
\(h_\text{i}\) : Coefficient d’échange thermique de surface intérieure
\(h_\text{e}\) : Coefficient d’échange thermique de surface extérieure
Complément :
Les différences de valeur entre \(R_\text{si}\) et \(R_\text{se}\) ne proviennent pas de la différence de température entre l’intérieur et l’extérieur mais bien des mouvements d’air plus importants à l’extérieur qu’à l’intérieur, ce qui influence le transfert de chaleur par convection
Question⚓
Q23. En déduire l’expression de la puissance thermique perdue par convection par un corps de surface \(S\). Préciser les unités.
Complément : Quelques valeurs de coefficients d’échange
La « gamme des valeurs » de \(h\) (unité \(\mathrm{W\cdot m^{-2} \cdot K^{-1} }\)) est :
convection libre (air) | \(5-25\) |
convection libre (eau) | \(100-900\) |
convection forcée (air) | \(10-500\) |
convection forcée (eau) | \(100-15\ 000\) |
convection forcée (huile) | \(50-2\ 000\) |
convection forcée (métaux fondus) | \(6\ 000-120\ 000\) |
eau bouillante | \(2\ 500-25\ 000\) |
vapeur d'eau se condensant | \(50\ 000-100\ 000\) |
💪 Exercice⚓
Question⚓
Les pertes de chaleur relatives à une pièce d'habitation sont estimées à \(4,0\ \mathrm{kW}\). On utilise, pour la maintenir à sa température interne de \(20\ \mathrm{^\circ C}\), des convecteurs (radiateurs) à la température de \(70\ \mathrm{^\circ C}\) (température de l'eau chaude). Le coefficient d'échanges superficiels de la surface d'échanges des convecteurs est estimé à \(10\ \mathrm{W\cdot m^{-2} \cdot K^{-1}}\).
Q24. Calculer la surface d'échanges S des radiateurs. (Réponse : \(8 \ \mathrm{m^2}\))
Solution⚓
Q24.
On a \(\Phi=4,0\ \mathrm{kW}\) et \(\varphi=h\times \left( T_\text{c} - T_\text{f} \right)\) avec \(T_\text{c}=70,0\ \mathrm{^\circ C} \)et \(T_\text{f}=20,0\ \mathrm{^\circ C}\) et \(h=10\ \mathrm{W\cdot m^{-2} \cdot K^{-1}}\).
Or \(\varphi=\dfrac{\Phi}{S}\), donc :
\(\dfrac{\Phi}{S}=h\times \left( T_\text{c} - T_\text{f} \right)\)
\(S=\dfrac{\Phi}{h\times \left( T_\text{c} - T_\text{f} \right)}\)
\(S=\dfrac{4,0\cdot 10^{3}}{10 \times \left( 70 - 20\right)}=8 \ \mathrm{m^2}\)
☀️ Les transferts thermiques par rayonnement⚓
Approche qualitative
Le rayonnement est un mode de transfert particulièrement important dans de nombreuses situations industrielles à hautes températures (fours par exemple) mais aussi géophysiques (refroidissement nocturne de la Terre, d’une piscine ou d’une habitation, dégel d’une route). Le rayonnement est à la base de nombreuses méthodes de mesures de température (caméra infra-rouge) qui sont non-intrusives et permettent d’opérer à distance, d’où l’importance d’étudier soigneusement le rayonnement.
Un corps chaud va perdre de l’énergie thermique par rayonnement au profit d’un corps plus froid, comme l’air la nuit ou en journée l’hivers.
L’onde thermique se propage à la vitesse de la lumière, c’est une onde électromagnétique.
L’onde émise transporte avec elle de l’énergie. Lorsqu’elle est émise par un corps radiant, celui-ci perd donc un certain flux d’énergie \(\large \Phi\) (Watt). De même, un corps frappé par cette onde électromagnétique reçoit de l’énergie :
Tout corps rayonne (donc perd) de l’énergie, mais les corps froids en émettent moins qu’ils n’en reçoivent…
Définition : Loi de Stephan-Boltzmann (1879-1884)
Tout corps, porté à une température supérieure à \(0\ \mathrm{K} \left(=-273,15\ \mathrm{^\circ C} \right)\) va émettre un rayonnement électromagnétique polychromatique (une multitude de radiations de longueurs d’onde différentes). On appelle émittance, noté \(\large \mathbf M\) , l’énergie émise par seconde et par unité de surface \(\left( \mathrm{m^2} \right)\)par ce corps.
À température ambiante, le rayonnement électromagnétique se situe dans le domaine des infrarouges.
L’émittance rayonnée par unité de surface est donnée par la relation :
\(\large \mathbf M\) : Emittance en \(\mathrm{W \cdot m^{-2}}\).
\(\large \mathbf \sigma\) : constante de stephan \((\sigma = 5,67 \cdot 10^{-8}\ \mathrm{W\cdot m^{-2} \cdot K^{-4}})\)
\(\large T\) : Température du corps qui rayonne en kelvin \(\mathbf K\)
Ce coefficient d’échange \(\mathbf{h}\) tient compte des différentes propriétés physiques et cinématiques du fluide léchant la paroi.
Question⚓
Q25. Comment calculer l’émittance totale (appelée aussi puissance totale, notée \(P\), exprimée en \(\mathrm W\)) émise par un corps de surface donnée \(S\) ?
☀️ Les transferts thermiques par conduction, rayonnement et convection⚓
Définition : Résistance thermique globale
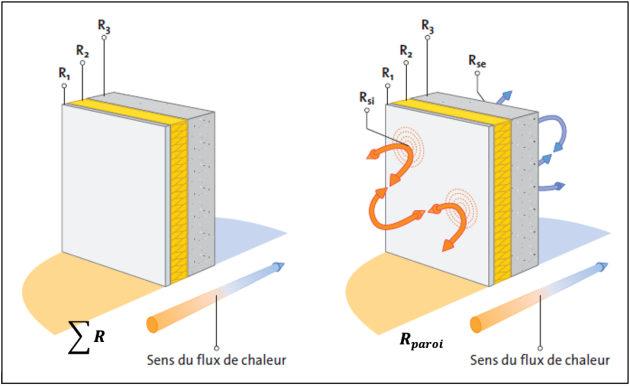
La résistance thermique totale d’une paroi homogène caractérise la somme des transferts de chaleur réalisés par conduction au sein des matériaux et des échanges thermiques superficiels réalisés par convection et rayonnement. Elle se calcule en additionnant les résistances thermiques des différents constituants de la paroi et les résistances superficielles correspondantes et s’exprime en \(\mathrm{m^{2} \cdot \mathrm{^\circ C} \cdot W^{-1} }\).