Problématique :
Comment varie la température d'un corps en fonction de l'énergie reçue ?
🥼 Expérience n°1⚓
Objectif de cette partie, répondre à la question :
Comment varie la température d'une masse d'eau en fonction de l'énergie reçue ?
Rappel : L'effet Joule [Document A.1]
L'effet Joule est un effet thermique qui se produit lors du passage du courant électrique dans un conducteur. Il se manifeste par une augmentation de l'énergie interne du conducteur et donc de sa température. Le conducteur transforme ainsi un travail électrique \(\mathbf{W}\) en énergie thermique \(\mathbf{Q}\).
L'effet Joule peut dans certains cas être un effet recherché pour produire de la chaleur (radiateur électrique, chauffe-eau, ...). Dans d'autres cas, il est responsable de pertes d'énergie et d'élévation indésirable de la température du milieu (processeur d'ordinateur, transformateur, ...).
Avec :
\(\mathbf{P}\) : puissance électrique en \(\mathbf{W}\)
\(\mathbf{U}\) : tension électrique en \(\mathbf{V}\)
\(\mathbf{I}\) : intensité du courant électrique en \(\mathbf{A}\)
Rappel : Puissance et travail électrique [Document A.2]
Le travail électrique \(\mathbf{W}\) apporté à un système est calculé à partir de la puissance électrique \(\mathbf{P}\) :
Avec :
\(\mathbf{W_{el}}\) : travail électrique en \(\mathbf{W}\)
\(\mathbf{P}\) : puissance électrique en \(\mathbf{W}\)
\(\mathbf{\Delta t}\) : intervalle de temps en \(\mathbf{s}\)
Rappel : Le calorimètre [Document A.3]
Le calorimètre est une enceinte isolée[*]. Il n'y a ainsi aucun échange de matière et d'énergie (travail ou chaleur) entre le milieu extérieur et les corps intérieurs et lui-même. Une résistance chauffante peut-être placée dans le calorimètre de façon à produire de la chaleur à l'intérieur de celui-ci lorsque celle-ci est reliée à un générateur.
❔ Questions préliminaires⚓
On considère le système {résistance}.
Question⚓
Q1. Compléter le schéma ci-contre illustrant les échanges énergétiques entre le système résistance et l'extérieur. On admettra que le travail électrique \(\mathbf{W_{el}}\) reçu est intégralement transformé en énergie thermique \(\mathbf{Q}\).
Question⚓
Q2. Donner l'expression littérale du travail électrique \(\mathbf{W_{el}}\) reçu et de l'énergie thermique \(\mathbf{Q}\) produite par le système résistance en fonction de \(\mathbf{U}\) , \(\mathbf{I}\) et \(\mathbf{\Delta t}\) .
🧪 Partie expérimentale⚓
Question⚓
Q3. Proposer et réaliser un protocole expérimental permettant de mesurer l'élévation de la température en fonction du temps de \(400\; mL\) d'eau placés dans un calorimètre. Ce dernier dispose d'une résistance produisant de l'énergie thermique par effet Joule lorsqu'elle est reliée à un générateur. Le montage doit permettre de mesurer à la fois la tension aux bornes du conducteur ohmique et l'intensité la traversant.
Les valeurs de températures peuvent être prises toutes les minutes pendant environ 10 minutes.
Il faudra noter les valeurs mesurées dans les tableaux de valeurs ci-dessous.
Solution⚓
Q3.
Les valeurs en rouge sont celles que j'ai obtenue lorsque j'ai fait l'expérience, vos valeurs à vous seront probablement différentes.
→ Peser le bol du calorimètre sec et vide, puis introduire 100 mL d'eau distillée, et repeser (TARE) le bol du calorimètre afin d'avoir exactement la masse d'eau introduite.
→ Placer le thermomètre dans le bol et noter la valeur de \({\color{red} \theta_{i}=23,05\; ^\circ \text{C}}\)
→ Placer la résistance dans le bol, et le raccorder au générateur et laisser l'équilibre thermique se faire.
→ Lancer le chronomètre dès que le générateur est allumé et que le courant passe, et relever la température toutes les 30 s pendant 15 minutes.
→ Noter la valeur de la tension et de l'intensité : \({\color{red} U=7,80 \text{ V}}\) et \({\color{red} I=1,86 \text{ A}}\)
→ Bien agiter le mélange à l'aide de l'agitateur. \({\color{red} \theta_{i}=28,1\; ^\circ \text{C}}\)
Tableau de mesure pour une masse d'eau de 400 g :
\(\mathrm{\Delta t \left(en\; s\right)}\) | 0 | 60 | 120 | 180 | 240 | 300 | 360 | 420 | 480 | 540 | 600 |
|---|---|---|---|---|---|---|---|---|---|---|---|
\(\mathrm{\theta \left ( en \;°C \right)}\) | 23,05 | 23,5 | 24 | 24,6 | 25,0 | 25,6 | 26,1 | 26,6 | 27,0 | 27,5 | 28,1 |
\(\Delta\theta=\theta-\theta_i\) \(\mathrm{\left(en\; °C \right)}\) | 0 | 0,45 | 0,95 | 1,55 | 1,95 | 2,55 | 3,05 | 3,55 | 3,95 | 4,45 | 5,05 |
\(\textrm{Énergie reçue}\; Q\) \(\mathrm{\left(en \;J\right)}\) | 0 | 870,5 | 1741 | 2611 | 2482 | 4352 | 5223 | 6093 | 6964 | 7834 | 8705 |
Conseil :
Bien penser à homogénéiser le mélange grâce à l'agitateur incorporé.
Complément : Tableaux de valeur
\(\mathrm{\Delta t \left(en\; s\right)}\) | |||||||
|---|---|---|---|---|---|---|---|
\(\mathrm{\theta \left ( en \;°C \right)}\) | |||||||
\(\Delta\theta=\theta-\theta_i\) \(\mathrm{\left(en\; °C \right)}\) | |||||||
\(\textrm{Énergie reçue}\; Q\) \(\mathrm{\left(en \;J\right)}\) |
\(\mathrm{\Delta t \left(en\; s\right)}\) | |||||||
|---|---|---|---|---|---|---|---|
\(\mathrm{\theta \left ( en \;°C \right)}\) | |||||||
\(\Delta\theta=\theta-\theta_i\) \(\mathrm{\left(en\; °C \right)}\) | |||||||
\(\textrm{Énergie reçue}\; Q\) \(\mathrm{\left(en \;J\right)}\) |
Question⚓
Q4. En utilisant un logiciel tableur-grapheur (comme Regressi), compléter la dernière ligne des tableaux de mesure en calculant l'énergie reçue par l'eau. On suppose que toute l'énergie fournie par la résistance est transférée à l'eau.
Question⚓
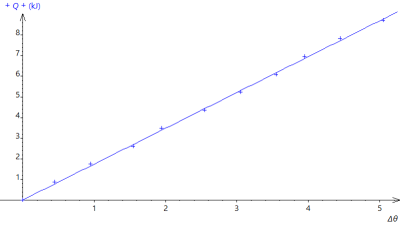
Q5. Tracer et modéliser la courbe représentant \(Q\) (l'énergie thermique reçue par l'eau assimilée à l'énergie électrique consommée par le thermoplongeur) en fonction de la variation \(\Delta \theta\) de température.
Solution⚓
Q5. Vous devriez essayer des modélisations du logiciel en pensant comment sont mis les points les uns par rapport aux autres.
Exemple de graphique obtenu avec les valeurs du tableau de mesure de la question Q3 pour 400 g d'eau.
Résultats de la modélisation (valeur du coefficient directeur de la droite obtenue) :
Question⚓
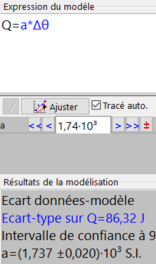
Q6. Quelle courbe obtenez-vous ? Commenter. Il faudra bien relever les paramètres de la modélisation.
Solution⚓
Q6. Vous devriez avoir obtenu une droite passant par l'origine. Il y a donc proportionnalité entre l'énergie thermique reçue par l'eau et la variation de température \(\Delta \theta\).
Le coefficient directeur de la droite est : \(a=1,74⋅10^3\). (valeur de la courbe précédente pour 400 g d'eau.)
🥼 Expérience n°2⚓
Objectif de cette partie, répondre à la question :
Pour une même variation de température, l'énergie reçue dépend-elle de la masse d'eau ?
🧪 Partie expérimentale⚓
En utilisant le même mode opératoire qu'à l'expérience n°1, choisir une masse d'eau parmi les valeurs suivantes et mesurer la durée pour élever sa température de \(\mathrm{2 \; °C}\).
Masse d'eau possible (partage des mesures entre plusieurs groupes) : 400 g ; 500 g ; 600 g.
Noter également les valeurs des grandeurs expérimentales mesurées :
\(m_{eau}=\text{ g}\) \(\theta_{i}=\text{ }^\circ \text{C}\) \(U=\text{ V}\) \(I=\text{ A}\)
Rassembler les valeurs obtenues par les différents groupes dans le tableau ci-dessous.
Masse d'eau \(\left ( en \; g \right )\) | ||||
|---|---|---|---|---|
Temps \(\left ( en \; s \right )\) | ||||
Énergie reçue \(\left ( en \; J \right )\) |
Question⚓
Q7. Tracer et modéliser la courbe représentant \(Q\) (l'énergie thermique reçue par l'eau assimilée à l'énergie électrique consommée par le thermoplongeur) en fonction de la masse \(m\) pour augmenter la température de l'eau de \(\mathrm{2 \; °C}\).
📝 Explications avec la variation d'énergie interne⚓
Ce résultat peut se généraliser pour des corps solides ou liquides.
Définition :
Lorsque la température d'un corps solide ou liquide varie d'une valeur initiale \(\theta_i\) à une valeur finale \(\theta_f\), la quantité de chaleur \(Q\) (ou énergie thermique) transférée, égale à la variation d'énergie interne \(\Delta U\), est définie par :
Avec :
\(\Delta U\) : variation d'énergie interne \(\left(en \; J\right)\)
\(m\) : masse du corps \(\left(en \; kg\right)\)
\(c\) : capacité thermique massique \((en \; J.kg^{-1}.^\circ \text{C }^{-1}\) ou \(\; J.kg^{-1}.K^{-1} )\)
\(\Delta \theta\) : variation de température \(\left(en \; ^\circ \text{C } ou \; K\right)\)
Attention : Remarque importante
Dans le cas de la matière condensée (état où les atomes sont en contact les uns avec les autres : matière liquide ou solide), le volume varie très peu avec la température comparativement au gaz. Il en résulte que les travaux des forces de pression sont la plupart du temps négligeables : donc \(W \approx 0 \;J\).
Complément : La capacité thermique massique [Document C.1]
Certains corps peuvent accumuler davantage d'énergie que d'autres : leurs capacités thermiques massiques sont différentes.
Tableau d'ordre de grandeur de capacités thermiques massiques à température ambiante :
En construction de bâtiments, les murs accumulateurs d'énergie doivent avoir des masses importantes (béton, pierre ou briques pleines) pour accumuler une grande quantité d'énergie.
Question⚓
Q11. En utilisant les résultats expérimentaux de la 1ère expérience (Q2 & Q5 & Q6 (partie A.) notamment la courbe obtenue, déterminer la valeur expérimentale \(\left(c_{eau} \right )_{exp}\) de la capacité thermique de l'eau en considérant que toute l'énergie fournie par le conducteur ohmique est transférée à l'eau.
Solution⚓
On a vu en Q2 que l'eau recevait une énergie Q. Et d'après la question Q13, l'énergie qui sert à augmenter la température de l'eau de \(\Delta \theta\) s'écrit : \(Q=m\cdot {\left( c_{eau} \right )}_{exp} \cdot \Delta \theta\).
Or la courbe \(Q=f \left( \Delta \theta \right )\) est une droite passant par l'origine d'équation \(Q=a \times \Delta \theta\).
On peut donc identifier \(a=m\cdot {\left( c_{eau} \right )}_{exp}\), d'où :
\({\left( c_{eau} \right )}_{exp}=\frac{a}{m}=\frac{1,74⋅10^3}{400⋅10^{-3}}=4,35⋅10^3 \; \mathrm{J.kg^{-1}.K^{-1}}\)
Complément : Incertitude relative d'une mesure : r [Document C.2]
L'incertitude relative, ou écart relatif, est un indicateur de la qualité et de la précision de la mesure.
Lorsque la grandeur mesurée m possède une valeur de référence connue, on calcule l'incertitude relative ainsi :
Les incertitudes relatives sont en général exprimées en pourcentage, il faudra donc l'écrire en pourcentage.
Plus r est petit et plus la mesure est précise.
On considère que si \(r<0,01\) (soit \(r<1\, \%\)) la mesure est de bonne qualité.
Question⚓
Q12. Calculer l'écart relatif de votre capacité thermique massique de l'eau expérimentale par rapport à la valeur théorique fournie dans le Doc.C-1 puis commenter le résultat obtenu en réfléchissant aux potentielles sources d'erreurs et à ce qu'on aurait négligé lors de l'expérience.
Solution⚓
Q12.
Sur une autre série de mesure (avec un autre conducteur ohmique, j'ai trouvé un écart de 11,2 %.
Nous avons un écart assez faible de 4 %. La mesure semble convenable.
Cependant, cet écart (et celui de l'autre série de mesure) ne peut s'expliquer uniquement par un manque de précision des mesures aux multimètres et de la mesure de température.
Dans cette étude nous n'avons tenu compte que de l'échange d'énergie entre le conducteur ohmique et l'eau. Or l'eau n'est pas le seul système à s'échauffer sous l'effet du conducteur ohmique. En effet, le calorimètre ainsi que ses accessoires voient leur température augmenter. De plus, le calorimètre n'est pas parfaitement isolé, il perd forcément de l'énergie vers le milieu extérieur.
Ce sont ces deux derniers points qui expliquent la variation entre la valeur expérimentale et la valeur théorique.