Objectif
Cette activité va vous permettre de découvrir le principe de la distribution du réseau d'eau dans un immeuble, de construire à partir des informations contenues dans les documents une expérience afin d'établir la loi de l'évolution de la pression d'un fluide en fonction de la hauteur (principe fondamentale de l'hydrostatique).
L'illustration via un cas pratique avec une problématique concrète va vous permettre de rédiger une synthèse pour argumenter sur la solution à retenir.
Introduction
Réunis en conseil syndical pour voter un projet de rénovation du circuit d'eau potable dans un immeuble, les propriétaires des appartements s'interrogent sur la nécessité d'installer des réducteurs de pression pour leur projet.
📄 Documents⚓
Complément : Quelques normes [Document n°1]
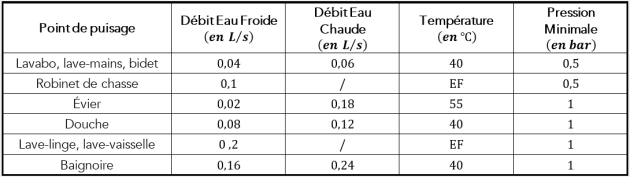
Pour garantir le confort de distribution de l'eau potable, l'installation sanitaire à l'intérieur du bâtiment doit tenir compte des exigences de pression, de débit et de température demandées.
Ainsi, pour qu'un robinet soit fonctionnel il doit délivrer un débit minimal, ce qui implique d'avoir en amont du robinet une pression minimale qui dépend du point de puisage.
Complément : La pression relative (ou effective) [Document n°2]
Un pressiomètre est un capteur de pression qui mesure une pression absolue \(p_\mathrm{abs}\) en hectopascal \(\left(hPa\right)\).
La pression absolue est la pression mesurée par rapport au vide absolu (c'est à dire l'absence totale de matière). Elle est toujours positive.
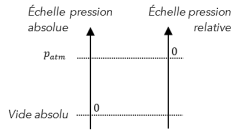
La pression relative \(p_\mathrm{rel}\) se définit par rapport à la pression atmosphérique existant au moment de la mesure.
 |
La relation qui lit les deux pressions est : \[\fbox{$ {\Large {\text{ } p_{\text{abs}} = p_{\text{rel}} + p_{\text{atm}} \text{ } } } $}\]
On rappelle : \(1,0\ bar=1\ 000\ hPa\).
Complément : Pression et réducteur de pression dans un immeuble [Document n°3.a]
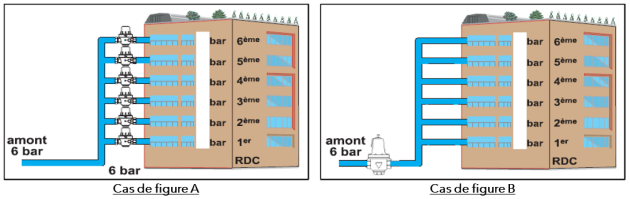
Dans un immeuble, on considère une hauteur de \(3\ m\) pour chaque étage à partir du rez-de-chaussée RDC. Deux solutions ont été retenues par le conseil syndical : soit la pose de plusieurs réducteurs de pression à chaque étage (cas de figure A), soit la pose d'un seul au RDC (cas de figure B).
Réducteurs de pression
Comme son nom l'indique, le réducteur de pression permet de diminuer la pression de l'eau qui arrive dans le réseau d'eau. Il protège toute l'installation des problèmes dus à un excès de pression : bruits dans les canalisations, coups de bélier, éclaboussures, usures prématurées des appareils électroménagers et des robinetteries. Une pression de 3 bars est recommandée.
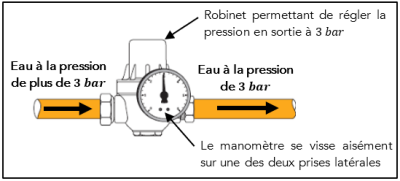
Il existe des modèles à pression réglable munis de manomètre comme celui présenté ci-dessous dans lequel une membrane intérieure commande un clapet, régulant ainsi le débit de l'eau et modifiant la pression en tournant robinet.
D'après http://conseils.xpair.com/...
📌 Problématique⚓
Dans le cas de leur immeuble d'habitation de 6 étages, la pression du réseau d'eau délivrée est de \(6\ bar\) et la pression souhaitée dans chaque appartement est de 3\ bars pour répondre aux exigences du Doc.1. Il apparaît donc nécessaire de poser un ou plusieurs réducteurs de pression dans l'immeuble.
Méthode : La problématique
Vous devez aider le conseil syndical à faire le bon choix :
→ Les étages seront-ils tous correctement desservis en pression dans les deux cas de figure du Doc.3 ?
→ Déterminer la solution que le conseil syndical devrait retenir en justifiant votre choix.
🧪 Mise en œuvre expérimentale et questions⚓
Complément : Matériels à votre disposition
Une colonne remplie d'eau (une grande éprouvette graduée) : Le lycée ne possède pas un tuyau aussi long que 6 étages rempli d'eau !!!
Une règle graduée et du scotch.
Une baguette en verre reliée à un capteur de pression absolue \(p_{\text{abs}}\). Grâce à ce dispositif vous pouvez mesurer la pression en n'importe quel point de la colonne d'eau.
Méthode : Expérimentation (RÉA)
→ Mesurer différentes pressions absolues \(p_{\text{abs}}\) en \(\mathrm{hPa}\) pour différentes hauteurs \(h\) en mètre. Présenter les résultats sous forme de tableau.
⚠ La hauteur \(h\) sera mesurée en partant de la surface en contact avec l'air pour faciliter la compréhension.
→ À partir de vos relevés, tracer la pression relative \(p_\text{rel}\) en fonction de la hauteur \(h\).
Exemple : Tableau de valeurs
\(h \ (en\ m)\) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
\(p_\text{abs} \ (en\ Pa)\) | |||||||||
\(p_\text{rel} \ (en\ Pa)\) |
Question⚓
Q1. (ANA) Comment varie la pression absolue en un point de l'eau en fonction de la hauteur \(h\) de la colonne d'eau au-dessus de ce point ?
Question⚓
Q2. (ANA/RÉA) À partir de votre courbe, donner une relation entre la pression relative \(p_{\text{rel}}\) en \(\mathrm{Pa}\) et la hauteur d'eau \(h\) en \(\mathrm{m}\).
Question⚓
Q3. (ANA/RÉA) Montrer qu'une variation de hauteur de \(3\ \mathrm{m} \), correspond à une variation de pression de \(0,3\ \mathrm{bar} \).
Aide : il faudra exprimer la pression en \(\mathrm{hPa}\) puis la convertir.
Question⚓
Q4. (RÉA) Compléter le Doc.3 en indiquant pour les deux cas de figure la pression à chaque étage avant et après le réducteur de pression.
Question⚓
Q5. (COM) Répondre aux questions du conseil syndical sur le choix de l'installation. (Argumenter la réponse).
Question⚓
Q6. (ANA) Dans le cas de figure A, les réducteurs seront-ils tous réglés de la même façon ? Justifier.
👨🎓 Pour comprendre : Le principe fondamental de l'hydrostatique (ou statique des fluides)⚓
Complément :
L'expérience précédente a été réalisée dans le champ de pesanteur terrestre qui vaut \(g=9,81\ \mathrm{N.kg^{-1}}\). Le fluide utilisé sera considéré comme étant de l'eau pure de masse volumique[*] \(\rho\).
Question⚓
Q7. (RCO) Quelle est la masse volumique de l'eau pure en \(\mathrm{g.L^{-1}}\) puis en \(\mathrm{kg.m^{-3}}\) ?
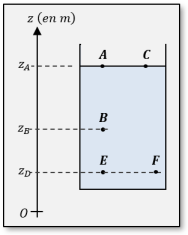
Complément : Schéma [Document n°4]
Dans le Doc.4 ci-contre, on regarde la pression en 5 points d'un réservoir ouvert contenant un fluide (comme de l'eau, ou de l'alcool, ou de l'huile...)
Question⚓
Q8. (ANA) Que peut-on dire de la pression au point A et de celle au point C dans le Doc.4 ? Même question pour les points E et F.
On peut en déduire la définition suivante :
Définition :
La pression est la même en tous points situés dans un même plan horizontal.
Question⚓
Q9. (ANA) À quoi est égale la pression absolue subie par le point B (faire une phrase) ?
🚩👨🎓 Énoncé du principe fondamental de l'hydrostatique⚓
Définition : 🚩 Énoncé du principe fondamental de l'hydrostatique
Dans un fluide incompressible de masse volumique \(\rho\), en équilibre dans le champ de pesanteur d'intensité \(g\), la pression \(p\) ne dépend que de l'altitude \(z\).
À l'intérieur du fluide, la relation entre les pressions et les altitudes s'écrit :
⚠ Attention ⚠
Cette relation n'est valable que si l'axe des altitudes \(\left(Oz\right)\) est orienté vers le haut.
Avec :
\(p_\mathrm{A}\) et \(p_\mathrm{B}\) : Pression en A et B en \(\mathrm{Pa}\)
\(\rho\) : masse volumique en \(\mathrm{kg.m^{-3}}\)
\(g\) : intensité de la pesanteur, sur Terre \(g=9,81\ \mathrm{N.kg^{-1}}\)
\(z_\mathrm{A}\) et \(z_\mathrm{B}\) : altitudes de A et B en \(\mathrm{m}\)
Question⚓
Q10. (ANA/RÉA) Dans le cas d'un axe des altitudes \(\left(Oz\right)\) orienté vers le haut, écrire le principe fondamental de l'hydrostatique sous la forme d'une variation de pression entre le point A et le point B.
Aide : une variation en physique c'est une différence de deux valeurs, elle se note avec le symbole \(\Delta\). Par exemple la variation de temps (appelée aussi durée) sera notée \(\Delta t\).

Complément : Remarque
On peut aussi trouver cette autre formulation : \(\mathrm{\Delta P}=\rho\times g\times h\) où\( h\) est la variation d'altitude et \(\mathrm{\Delta P}\) la variation de pression entre les deux points (A et B).
⚠ Attention, ici le \(h\) étant une hauteur, \(h\) est positif, il faut donc que la variation de pression \(\mathrm{\Delta P}\) soit correctement exprimée (la plus grande pression moins la plus petite) pour qu'elle soit elle aussi positive.
💪 Petits exercices pour s'entraîner⚓
🏋🏻 Exercice n°1⚓
Un nageur est à \(10\ m\) sous l'océan. Il plonge à \(20\ m\) de profondeur.
Complément :
On donne : \(p_\mathrm{atm}=1\ 013\ \mathrm{hPa}\) ; \(\rho_\mathrm{eau\ de\ mer}=1\ 025\ \mathrm{kg.m^{-3}}\) et \(g=9,81 \ \mathrm{N.kg^{-1}}\).
Question⚓
Question⚓
Q12. (RÉA) Calculer la surpression occasionnée par sa descente.
Aide : Une surpression est une variation de pression.
🏋🏻 Exercice n°2⚓
Complément :
On donne : \(\rho_\mathrm{air}=1,29\ \mathrm{kg.m^{-3}}\).
Question⚓
Q13. (RÉA) Calculer en \(\mathrm{Pa}\), puis en \(\mathrm{bar}\) la différence de pression en deux points situés dans l'air, dans deux plants horizontaux dont la dénivellation est de \(10\ \mathrm{m}\).
Aide: vous devez trouver \(\Delta p=1,27\ \mathrm{mbar}\)
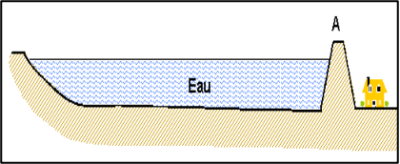
🏋🏻 Exercice n°3 : Barrage⚓
Complément :

Question⚓
Q15. (RCO) Comment évolue-t-elle le long d’un plan vertical ? Faire un schéma en faisant apparaître les forces pressantes agissant sur des éléments de parois, sans soucis d’échelle mais en respectant toutefois leur évolution.
Question⚓
Q16. (ANA) Pourquoi les barrages ont-ils une épaisseur plus importante en bas qu’en haut ?