❓ Qu’est-ce que le phénomène de dilatation ?⚓
Définition :
La dilatation thermique est l’expansion à pression constante du volume d’un corps occasionnée par son réchauffement, et inversement.
Complément : Schémas pour la question Q1.
Schéma A
Schéma B
〰 La dilatation linéique⚓
Complément : 📄 Le rail qui se déforme [Document n°1]
On observe qu’un rail s'allonge lorsque sa température augmente :


Un rail en acier de \(\mathbf{36\ \mathrm{m}}\) s’allonge de \(\mathbf{2\ \mathrm{mm}}\) si sa température augmente de \(\mathbf{5\ \mathrm{^\circ C}}\).
Un rail en acier de \(\mathbf{36\ \mathrm{m}}\) s’allonge de \(\mathbf{6\ \mathrm{mm}}\) si sa température augmente de \(\mathbf{15\ \mathrm{^\circ C}}\).
❔ Questions bonus (À faire chez soi 🏠)⚓
Complément :
Question⚓
Q7. (ANA) Expliquer son fonctionnement. (Aide : voir vidéo 1min18s à 1min25s)
Solution⚓
Q7.
Deux rails sont accolés : celui qui est fin est à l’intérieur de la voie et l’autre plus épais sur l’extérieur. Lorsque les rails vont se dilater sous l’effet de la chaleur, ils vont pouvoir coulisser l’un contre l’autre au lieu de se déformer latéralement comme sur les images du Document 1.
⚙️ Mise en évidence du phénomène de dilatation des matériaux⚓
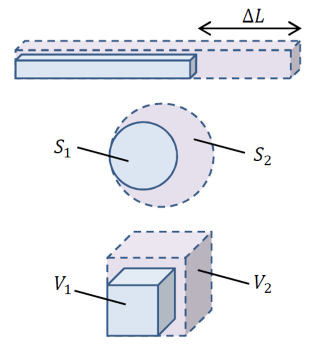
Lorsqu’un corps se dilate, ses dimensions augmentent dans toute s les directions : c’est son volume qui augmente. Dans le cas d’un solide de forme allongée (barre, tige), la dilatation se manifeste principalement par une variation de longueur.
Complément : 🔎 Une petite expérience montrant la dilatation linéique [Document n°2]

Une tige métallique est fixée d’un côté et est posée sur une tige libre de tourner autour de son axe et dont une bande de papier est solidaire.

Sous l’effet de la dilatation du fil, la tige tourne autour de son axe. Cette rotation est rendue visible par l’inclinaison de la bande de papier.

\(\leftarrow\) le QR-Code ci-contre vous amènera à une petite vidéo de cette expérience.
Question⚓
Q8. (ANA/APP) Expliquer le fonctionnement du dispositif expérimental et décrire protocole opératoire
🧮 Calcul d'une dilatation linéique⚓
Complément : 📌 Comment calculer la dilatation linéique d’un corps ? [Document n°3]
Pour calculer la dilatation linéique d'un corps (ou son allongement linéaire), on utilise les grandeurs suivantes :
\(\Delta\ell\) est la variation de longueur en \(\mathrm{m}\) ;
\(\Delta\theta=\theta_f-\theta_i\) est la variation de température en \(\mathrm{^\circ C}\) ou \(\mathrm{K}\) entre la température initiale \(\theta_i \)et la température finale \(\theta_f\) ;
\(\ell\) est la longueur initiale de l’élément qui se dilate en \(\mathrm{m}\) ;
\(\alpha\) est le coefficient de dilatation linéaire en \(\mathrm{^\circ C}^{-1}\) ou \(\mathrm{K}^{-1}\). Ce coefficient dépend du matériau et de la température
Question⚓
Q11. (RÉA) Un rail en acier a une longueur de \(80\ \mathrm{m}\) à \(0\ \mathrm{^\circ C}\). Quelle est la valeur de son allongement à \(50\ \mathrm{^\circ C} \) ? à \(-20\ \mathrm{^\circ C}\) ?
Solution⚓
Q11.
À \(50\ \mathrm{^\circ C} \) :
\(\Delta\ell=\alpha\times\ell\times\Delta\theta=1,20\cdot10^{-5}\times80\times\left(50-0\right)\color{blue}=4,8\cdot{10}^{-2}\ \ \mathrm{m}\color{black}=4,8\ \ \mathrm{cm}\)
À \(-20\ \mathrm{^\circ C} \) :
\(\Delta\ell=1,20\cdot10^{-5}\times80\times\left(-20-0\right)\color{blue}=-1,9\cdot{10}^{-2}\ \ \mathrm{m}\color{black}=-1,9\ \ \mathrm{cm}\)
Question⚓
Q12. (ANA/APP) Si on observe une voie de chemin de fer, on note qu’en général, les rails ne sont pas jointifs. Pourquoi ?
Solution⚓
Q12.
Sous l’action du soleil, ou de l’échauffement dû au passage des rames, les rails peuvent se dilater de plusieurs centimètres. Il faut laisser une place suffisante pour que cette dilatation puisse avoir lieu, sinon, il y aurait déformation des rails et risque de déraillement. En revanche, lors des périodes de grand froid, l’intervalle entre les rails augmente, mais cela est moins gênant car les roues ont un diamètre suffisant pour absorber cette discontinuité.
Question⚓
Q13. (RÉA) Déterminer la longueur finale d’une barre de fer de \(100\ \mathrm{cm}\) si sa température augmente de \(100\ \mathrm{^\circ C}\).
Solution⚓
Q13.
La dilatation linéique de cette barre vaut :
\(\Delta\ell=\alpha\times\ell\times\Delta\theta=1,1\cdot10^{-5}\times100\cdot{10}^{-2}\times100\color{blue}=1,1\cdot{10}^{-3}\ \mathrm{m}\color{black}=1,1\ \ \mathrm{mm}=0,11\ \mathrm{cm}\)
La longueur finale de cette barre vaut donc : \(\ell_\text{finale}=\ell+\Delta\ell=100+0,11=100,11\ \mathrm{cm}\)
📝 Une application de la dilatation linéique (À faire chez soi 🏠)⚓
Complément :
Question⚓
Q14. (ANA/APP) Décrire et expliquer les observations faites à l’aide des schémas précédents.
Question⚓
Le bilame est utilisé dans les disjoncteurs thermiques et permet de couper facilement le contact en cas de surchauffe de l’appareil.
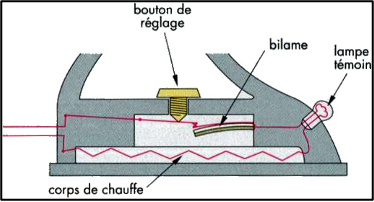
▲ Vue en coupe d’un fer à repasser simple
Q15. (ANA/APP) Expliquer comment le bilame peut servir de disjoncteurs dans le cas du fer à repasser ci-contre.
Solution⚓
Q15.
Lorsque le fer à repasser fonctionne il chauffe. Le bilame va donc se courber d’une certaine manière, ici vers le bas, du fait de sa composition. En cas de surchauffe, le bilame va ouvrir le circuit électrique causant alors l’interruption du chauffage par le corps de chauffe jusqu’à ce que la température redescende, fermant à nouveau le circuit.
Question⚓
Un thermomètre ci-contre, est en réalité constitué d’un bilame au bout duquel est fixé une aiguille (le bilame étant fixé au centre du cadran).
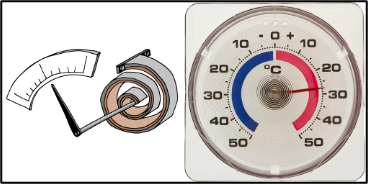
▲ Thermomètre de congélateur
Q16. (ANA/APP) Expliquer le fonctionnement de ce thermomètre.
Complément :
Le principe du bilame est aussi utilisé pour entre-ouvrir les fenêtres des serres en cas de forte chaleur.
〰 Dilatation surfacique⚓
Complément : 📌 La dilatation surfacique [Document n°4]
La dilatation agit comme un zoom : les creux aussi se dilatent.

Pour calculer la dilatation surfacique d'un corps, on utilise les grandeurs suivantes :
\(\Delta S\) est la variation de longueur en \(\mathrm{m}^2 \) ;
\(\Delta\theta=\theta_f-\theta_i\) est la variation de température en \(\mathrm{^\circ C}\) ou \(\mathrm{K}\) entre la température initiale \(\theta_i \)et la température finale \(\theta_f\) ;
\(S\) est la surface initiale de l’élément qui se dilate en \(\mathrm{m}^2\) ;
\(2\ \alpha\) est le coefficient de dilatation surfacique en \(\mathrm{^\circ C}^{-1}\) ou \(\mathrm{K}^{-1}\). (\(\alpha\) étant le coefficient de dilatation linéique).
〰 Dilatation Volumique⚓
Complément : 📌 La dilatation volumique [Document n°5]
Pour calculer la dilatation volumique d'un corps, on utilise les grandeurs suivantes :
\(\Delta V\) est la variation de longueur en \(\mathrm{m}³ \) ;
\(\Delta\theta=\theta_f-\theta_i\) est la variation de température en \(\mathrm{^\circ C}\) ou \(\mathrm{K}\) entre la température initiale \(\theta_i \)et la température finale \(\theta_f\) ;
\(V\) est la surface initiale de l’élément qui se dilate en \(\mathrm{m}³\) ;
\(3\ \alpha\) est le coefficient de dilatation volumique en \(\mathrm{^\circ C}^{-1}\) ou \(\mathrm{K}^{-1}\). (\(\alpha\) étant le coefficient de dilatation linéique).
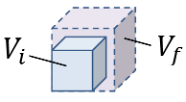
Le coefficient de dilatation volumique est fréquemment noté \(\gamma\). On a alors : \(\mathbf{\gamma=\color{blue}3\alpha}\).
Complément : 📄 Cas des liquides [Document n°6]
On utilise dans le plus souvent la dilatation volumique des liquides. La loi est la même que celles des solides, seules changent les valeurs du coefficient de dilatation, dont l’ordre de grandeur est de \({10}^{-3}\ \mathrm{K^{-1}}\).
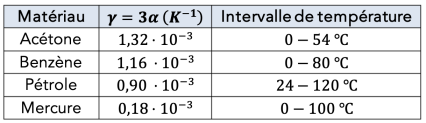
Lorsqu’on mesure la dilatation de liquide, il faut également prendre en compte la dilatation du solide qui le contient. Cependant, compte tenu de la valeur de leurs coefficients de dilatation respectifs (2 ordres de grandeur les sépare), on peut souvent négliger la dilatation du récipient.
💪 Petit exercice : Problème de réservoir et dilatation de l’essence⚓
Question⚓
Q18. (RÉA) Un réservoir d’automobile a un volume de \(45\ \mathrm{L}\) à \(0\ \mathrm{^\circ C}\). Quel volume d’essence pourra t-il contenir l’été lorsque la température est de \(40\ \mathrm{^\circ C}\) ? L’hiver, par une température de \(-10\ \mathrm{^\circ C}\) ?
Donnée : \(\alpha_\text{réservoir}=1,2\cdot 10^{-5}\ \mathrm{K}^{-1}\)
Solution⚓
Q18.
En été, la dilatation volumique vaut :
\(\Delta V_\text{été}=3\alpha_\text{réservoir}\times V \times\Delta \theta\)
\(\Delta V_\text{été}=3 \times 1,2 \cdot 10^{-5}\times45\cdot{10}^{-3}\times \left(40-0\right)\)
\(\Delta V_\text{été}=6,5\cdot10^{-5}\ \mathrm{m^3}\)
\(\Delta V_\text{été}=6,5\cdot10^{-2}\ \mathrm{dm^3}=6,5\cdot10^{-2}\ \mathrm{L}\)
Le volume d’essence pouvant être contenu en été vaut donc : \(V_\text{été}=V_i+\Delta V_\text{été}=45,065\ \mathrm{L}\)
En hiver, la dilatation volumique vaut :
\(\Delta V_\text{hiver}=3\times1,2\cdot10^{-5}\times45\cdot{10}^{-3}\times\left(-10-0\right)\)
\(\Delta V_\text{hiver}=-1,6\cdot10^{-5}\ \mathrm{m^3}\)
\(\Delta V_\text{hiver}=-1,6\cdot10^{-2}\ \mathrm{dm^3}=-1,6\cdot10^{-2}\ \mathrm{L}\)
Le volume d’essence pouvant être contenu en hiver vaut donc : \(V_\text{hiver}=V_i+\Delta V_\text{hiver}=44,984\ \mathrm{L}\)
Attention : Remarque
En fait, les choses sont un peu plus compliquées car l’essence aussi se dilate et on devrait en tenir compte pour évaluer la quantité exacte de carburant que l’on peut introduire.
Question⚓
Dans l’industrie pétrolière, une cuve contient, à \(0\ \mathrm{^\circ C}\), \(400\ 000\ \mathrm{L}\) d’essence. Le soleil frappant la cuve, la température de l’essence atteint la température de \(33\ \mathrm{^\circ C}\).
Q19. (RÉA) Calculer l’augmentation du volume d’essence. Commenter.
Donnée : \(\alpha_\text{essence}=4,0\cdot 10^{-4}\ \mathrm{K}^{-1}\)
Solution⚓
Q19.
\(\Delta V=3\times4,0\cdot10^{-4}\times400\ 000\cdot{10}^{-3}\times\left(33-0\right)=15,84\ \mathrm{m^3}=15,84\cdot{10}^3\ \mathrm{L}=15\ 840\ \mathrm{L}\)
Les professionnels de l’industrie pétrolière doivent tenir compte de la dilatation lorsqu’ils remplissent les cuves… Il ne faut donc pas remplir à ras-bord la cuve.
💪 Petit exercice : La masse volumique⚓
Vous savez tous que la masse d’un litre d’eau est un kilogramme et que si vous portez deux litres d’eau, vous portez un échantillon d’eau de deux kilogrammes. Mais pourquoi le savez-vous ? … Parce que vous connaissez déjà tout, ou presque, des grandeurs physiques importantes.
Définition :
Considérons un échantillon de matière (dans l’un quelconque de ses trois états : solide, liquide, gazeux) de masse \(m\) et de volume \(V\), et ceci dans des conditions de température et de pression données. Si la matière est homogène, alors le rapport \(m/V\) est indépendant de l’échantillon prélevé d’une part, et est caractéristique de la nature de la matière considérée d’autre part. Ce rapport caractéristique prend le nom de « masse volumique » et se note généralement « \(\rho\) » (lire « rho »).
Question⚓
Q20. (ANA) Donner la formule permettant de calculer la masse volumique d’un corps, ainsi que les unités associées, dans la zone de définition suivante.
Solution⚓
Q20.
\(\rho\) : masse volumique en \(\mathrm{kg\cdot m^{-3}}\) ou en \(\mathrm{g\cdot L^{-1}}\)
\(m\) : masse de l’échantillon en \(\mathrm{kg}\) ou en \(\mathrm{g}\)
\(V\) : volume de l’échantillon en \(\mathrm{m^{3}}\) ou en \(\mathrm{L}\)
Définition : 📌 La masse volumique
🎁 Bonus – Pour votre culture⚓
Complément : 📄 Quelques applications de la dilatation volumique pour les liquides
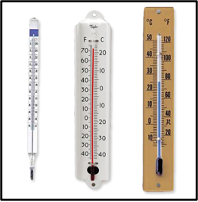
Les thermomètres à dilatation
En application immédiate de la loi précédente, on pense aux thermomètres à dilatation : le thermomètre à alcool et le thermomètre au mercure (attention : le mercure se solidifie à \(-39\ \mathrm{^\circ C}\) et l’alcool s’évapore à \(85\ \mathrm{^\circ C}\)). Le mercure se dilate 7 fois plus que le verre, et l’alcool, 50 fois plus.
Voir exercice n°7.
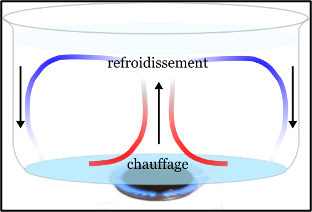
L’eau qui se trouve en contact de la source de chaleur s’échauffe, se dilate et sa masse volumique diminue ; elle devient moins dense et tend à monter dans le liquide. Elle est remplacée par l’eau froide, plus dense, qui descende le long des parois du récipient, qui à son tour, s’échauffe. Il se crée, dans le liquide, des courants de convection qui permettent l’échauffement de toue la masse d’eau.
Ainsi, l’eau chaude du chauffage central peut monter dans les étages sans aucun moyen mécanique à condition que la chaudière soit dans la partie basse du bâtiment. L’eau se dilate dans la chaudière et s’élève vers les radiateurs où elle se refroidit, voit sa masse volumique augmenter et redescend vers la chaudière. (En réalité, pour faciliter ce mouvement, on ajoute une petite pompe au système, appelée accélérateur).
Le phénomène de convection explique aussi les vents et les mouvements du magma terrestre.
🏋🏻♂️ Exercices d’application sur la dilatation des corps⚓
💪 Exercice n°1 : S’exercer à trouver l’information et à argumenter⚓
Question⚓
Q23. (APP) Expliquer pourquoi les armatures en acier du béton armé ne se dissocient pas du béton lors des changements de températures.
Solution⚓
Q23.
Les armatures du béton armé sont en acier. L’acier et le béton ont le même coefficient de dilatation linéaire, donc le même coefficient de dilatation volumique. Ils vont donc se dilater de la même façon, c’est-à-dire que leur variation de volume sera identique. Donc les armatures ne vont pas se dissocier du béton lorsque la température va varier.
Question⚓
Q24.. (VAL) Quel peut-être le problème d’une cuve en acier contenant de l’eau ?
Solution⚓
Q24.
L’acier et l’eau ont des coefficients de dilatation linéaire très différents : celui de l’eau est au moins 10 fois plus grand que celui de l’acier. Donc lorsque la température va fortement augmenter, le volume d’eau va augmenter 10 fois plus que le volume que pourra contenir la cuve en acier qui va elle aussi se dilater.
💪 Exercice 2 : S’exercer à réaliser des calculs⚓
Question⚓
Q26. (RÉA) Une poutre en acier mesure 10,00 m à une température de 10 °C. Quel sera son allongement à une température de 50 °C ?
(Réponse : 4,8\ mm)
Question⚓
Q27. (RÉA) L’échelle de graduation d’un mètre à mesurer en acier est gravée à 15 °C. Quelle est l’erreur commise sur une mesure de 60 cm à 30 °C ?
(Réponse : 0,11 mm)
Solution⚓
Q27.
L’erreur commise sur une mesure de \(60\ cm\) correspond à l’allongement de ces \(60\ cm\) mesurés à \(30\ \mathrm{^\circ C}\) :
\(\Delta\ell=\alpha\times\ell\times\Delta\theta=1,20\cdot10^{-5}\times60\cdot{10}^{-2}\times\left(30-15\right)=1,1\cdot{10}^{-4}\ \mathrm{m}=0,11\ \mathrm{mm}\)
L’erreur commise est donc de \(0,11\ \mathrm{mm}\).
Question⚓
Q28. (RÉA) La tour Eiffel, en acier, a une hauteur de \(320\ \mathrm{m}\) à \(20\ \mathrm{^\circ C}\) . Quelle est la variation de sa hauteur sur l’intervalle \(-20\ \mathrm{^\circ C}\) à \(35\ \mathrm{^\circ C}\) ? Quelle est sa hauteur maximale ?
(Réponse : –15,4 cm ; 5,76 cm ; 320,0576 m)
Solution⚓
Q28.
À \(-20\ \mathrm{^\circ C}\), la dilatation linéique vaut : \(\Delta\ell_{-20}=1,20\cdot10^{-5}\times320\times\left(-20-20\right)=-0,154\ m=-15,4\ \mathrm{cm}\)
À \(35\ \mathrm{^\circ C}\), la dilatation linéique vaut : \(\Delta\ell_{35}=1,20\cdot10^{-5}\times320\times\left(35-20\right)=0,0576\ m=5,76\ \mathrm{cm}\)
La hauteur maximale de la tour Eiffel est donc : \(\ell_{maxi}=\ell+\ell_{35}=320,0576\ \mathrm{m}\)
Question⚓
Q29. (RÉA) On pose une voie de chemin de fer à 15 °C avec des rails d’acier de 20 m de long. Quel est l’espace minimal requis entre les extrémités des rails si on s’attend à une température maximale de 35 °C ?
(Réponse : 4,8 mm)
Solution⚓
Q29.
Il faut calculer la dilatation linéique des rails à 35 °C, et laisser cet écart entre deux rails successifs :
\(\Delta\ell=1,20\cdot10^{-5}\times20\times\left(35-15\right)=4,8\cdot{10}^{-3}\ m=4,8\ \mathrm{mm}\)
Il faut donc laisser un espace minimal de 4,8 mm entre deux rails successifs.
Question⚓
Q30. (RÉA) La glace d’une vitrine est un rectangle de 4,00 m sur 2,50 m à 15 °C. Calculer l’accroissement de surface qui accompagne une élévation de température de 15 °C à 35 °C.
(Réponse : \(3,6\cdot{10}^{-3}\ m^2\))
Question⚓
Q31. (RÉA) Une plaque d’égout en fonte (disque) a un diamètre \(D\) égal à 0,50 m à 20 °C. Calculer sa surface à 43 °C.
(Réponse : \(0,196\ m^2\))
Solution⚓
Q31.
Calculons d’abord la variation de la surface : \(\Delta S=2\times1,05\cdot10^{-5}\times\left(\pi\times\dfrac{{0,50}^2}{4}\right)\times\left(43-20\right)=9,5\cdot{10}^{-5}\ m^2\)
La surface de la plaque d’égout à 43 °C vaut alors : \(S^\prime=S+\Delta S=\pi\times\dfrac{{0,50}^2}{4}+9,5\cdot{10}^{-5}=0,196\ \mathrm{m^2}\)
Question⚓
Q32. (RÉA) Une cuve d’eau de \(1\ \mathrm{m^{3}}\) passe de 4 °C à 35 °C. Calculer l’augmentation de volume d’eau correspondant.
Donnée :\( \alpha_{eau}=1,2\cdot10^{-4}\ \mathrm{^\circ C}^{-1}\)
(Réponse : 11,2 L)
💪 Exercice 3 : S’exercer analyser⚓
On se propose de comprendre pourquoi un chauffe-eau électrique goutte régulièrement lorsque le chauffage de l’eau a lieu.
Question⚓
Q34. (ANA/RÉA) Conclure quant au volume perdu, noté \(V_\text{pertes}\), d’eau s’échappant de la cuve lors de son chauffage de 15 °C à 80 °C sachant que le volume d’acier \(V_{15}\) de la cuve en acier à 15 °C est de 30 L (le même que celui de l’eau).
(Réponse : \(V_{pertes}=0,632\ L\\) ; Aide : calculer la dilatation de la cuve, puis celle du volume d’eau)
Donnée : \(\alpha_{eau}=1,2\cdot10^{-4}\ \mathrm{^\circ C}^{-1} \hspace{1cm} \alpha_{acier}=1,2\cdot10^{-5}\ \mathrm{^\circ C}-{-1}\)
💪 Exercice 4 : Vrai ou faux ? (RCO)⚓
💪 Exercice 5 : La lampe clignotante (à faire après avoir fait le bonus de la partie B. La dilatation linéique)⚓
Question⚓
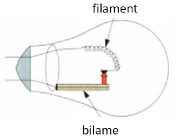
Q35. (ANA/COM) Expliquez le fonctionnement de la lampe clignotante ci-contre.
Solution⚓
Q35.
Lors du fonctionnement de l’ampoule, le filament chauffe et produit de la lumière lorsqu’il est parcouru par le courant électrique.
Le bilame va donc s’incurver vers le bas sous l’effet de l’augmentation de la température, ce qui va ouvrir le circuit électrique et donc la lampe ne produira plus de lumière, tant que la température ne sera pas redescendue suffisamment pour que le bilame reprenne sa forme initiale refermant le circuit et permettant à la lampe de reproduire de la lumière.
On a donc une lampe clignotante.
💪 Exercice 6⚓
Question⚓
Q36. (ANA/RÉA) Lors d’une élévation de température, l’arête de cette barre qui mesure 50 cm s’allonge de 0,1 mm. Calculer les allongements des autres arêtes en mm.
(Réponse : \(\Delta\ell_\text{arrête 1 cm}=0,002 mm\ \ ;\ \ \Delta\ell_\text{arrête 2 cm}=0,004 mm\))

Solution⚓
Q36.
On connait l’allongement de la grande arête et sa longueur initiale, mais on ne connait pas la variation de température qui engendre cette dilatation nu la matière de la barre… Il nous faut donc isoler ces deux grandeurs dans la formule : (on ne cherchera pas à déterminer séparément \(\alpha\) de \(\Delta\theta\)).
\(\Delta\ell=\alpha\times\ell\times\Delta\theta \Leftrightarrow \color{blue}\alpha\times\Delta\theta\color{black}=\dfrac{\Delta\ell}{\ell}=\dfrac{0,1}{50\cdot{10}^1}\color{blue}=2\cdot{10}^{-4}\)
Ainsi pour l’arête de 1 cm, son allongement vaut alors :
\(\Delta\ell_\text{arrête 1 cm} =\color{blue}\alpha\times\Delta\theta\color{black} \times \ell=\color{blue}2\cdot10^{-4}\times 1\cdot 10^{-2}\)
\(\Delta\ell_\text{arrête 1 cm} =2\cdot{10}^{-6}\ \mathrm{m}=0,002\ \mathrm{mm}\)
Et pour l’arête de 2 cm, son allongement vaut alors :
\(\Delta\ell_\text{arrête 2 cm} =\color{blue}\alpha\times\Delta\theta\color{black} \times \ell=\color{blue}2\cdot10^{-4}\times 2\cdot 10^{-2}\)
\(\Delta\ell_\text{arrête 2cm} =4\cdot{10}^{-6}\ \mathrm{m}=0,004\ \mathrm{mm}\)
💪 Exercice 7 : Le thermomètre⚓
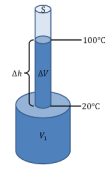
Un thermomètre est constitué d’une capsule de verre (pyrex) soudée à un tube très fin. Le volume intérieur de la capsule est de \(60\ \mathrm{mm^{3}}\) et la section intérieure du tube est de \(0,01\ \mathrm{mm^{2}}\) que l’on considérera constante même avec l’élévation de température. La capsule est remplie de mercure Hg qui, à \(20\ \mathrm{^\circ C}\), arrive au bas du tube.
Question⚓
Q37. (RÉA/COM) De combien le mercure s’élève-t-il dans le tube lorsque la température atteint 100 °C ? (Il faudra tenir compte de la dilatation du pyrex)
(Réponse : \(\mathrm{\Delta h}=8,06\ cm\) ; Aide : calculer dilatation du pyrex et du mercure du réservoir, puis exprimer le volume dans le tube en fonction des variables calculées)
Question⚓
Q38. (RÉA/COM) Vérifier l’affirmation concernant la section intérieure du tube.
Solution⚓
Q38.
\(S_{80}=S+\Delta S=S+2\alpha\times S\times\Delta\theta\)
\(S_{80}=1\cdot{10}^{-8}+2\times0,4\cdot10^{-5}\times1\cdot{10}^{-8}\times80\)
\(S_{80}=1,00064\cdot{10}^{-8}\ \mathrm{m^2}\approx1\cdot{10}^{-8}\ \mathrm{m^2}\)
La dilatation surfacique de la section du tube en pyrex est très très faible par rapport à la section, et donc on peut bien négliger la dilatation et considérer la section du tube constante.