Mathieu habite un studio dans un immeuble. Afin de gérer ses dépenses, il aimerait évaluer le coût du chauffage électrique sur une période d'un mois.
Complément : 📄 Document n°2 : Caractéristiques du studio et température
La température intérieure, dans le studio, est \(\large \mathrm{\theta_i=20\ \mathrm{^\circ C}}\). Cette température est la même dans les appartements voisins du même étage, des étages supérieurs et inférieurs, ainsi que dans le couloir.
La température extérieure est \(\large \mathrm{\theta_e=5,0\ \mathrm{^\circ C}}\).
L'épaisseur des murs est \(\large e_\mathrm{m}=20\ \mathrm{cm}\)
L'épaisseur du verre est \(\large e_\mathrm{V}=3\ \mathrm{mm}\).
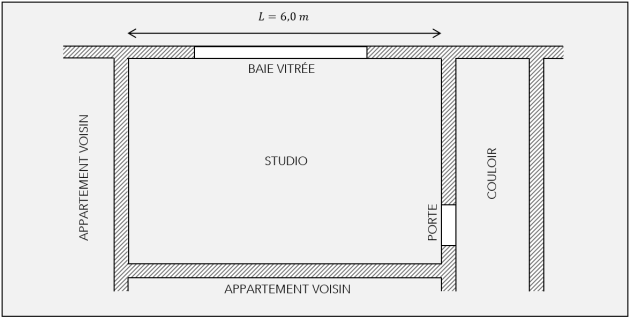
Les dimensions intérieures du studio sont :
longueur : \(\large L= 6,0\ \mathrm{m}\)
largeur : \(\large \ell =5,0\ \mathrm{m}\)
hauteur : \(\large h=2,5\ \mathrm{m}\)
La baie vitrée est rectangulaire et a pour dimensions :
largeur : \(\large \ell_\mathrm{V}=2,5\ \mathrm{m}\)
hauteur : \(\large h_\mathrm{V}=2,1\ \mathrm{m}\)
Complément : 📄 Document n°3 : Données
Coefficient d'échanges superficiels interne : \(\large h_\mathrm{i}=7,0\ \mathrm{W.K^{-1}.m^{-2}}\)
Coefficient d'échanges superficiels externe : \(\large h_\mathrm{e}=20\ \mathrm{W.K^{-1}.m^{-2}}\)
Conductivité thermique du verre : \(\large \lambda_\mathrm{V}=1,15\ \mathrm{W.m^{-1}.K^{-1}}\)
Conductivité thermique du matériau dont est constitué le mur : \(\large \lambda_\mathrm{m}=3,6\ \mathrm{W.m^{-1}.K^{-1}}\)
⚙️ Travail demandé⚓
Question⚓
Q1. (RCO) Rappeler les trois modes de transfert thermique et les décrire brièvement.
Solution⚓
A1-Q1.
Les trois modes de transfert thermique sont :
la convection : dans un fluide dont la température n'est pas homogène, la zone chaude moins dense que la zone froide s'élève. (La convection est donc un transfert thermique porté par un mouvement de matière.)
la conduction : essentiellement dans les solides (un peu dans les liquides), sans transport de matière, les constituants communiquent à leur voisin leur agitation thermique.
le rayonnement : tout corps émet un rayonnement en raison de sa température, ce transfert d'énergie ne nécessite pas de milieu matériel.
Pour les questions suivantes, il faudra s'aider des documents précédents et de ceux fournis en annexe (ouvrir le lien suivant dans un nouvel onglet : DOCUMENTS Annexes.pdf ).
Question⚓
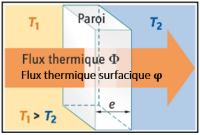
Q2. (APP/RÉA) Rappeler l'expression générale de la densité de flux thermique \(\large \mathrm{\varphi}\) (ou flux thermique surfacique) traversant une paroi simple homogène en fonction de la résistance thermique surfacique totale \(\large R_\mathrm{{totale}}\) de cette paroi et de la différence de température \(\large \mathrm{\Delta\theta}\) de part et d'autre de cette paroi. Accompagner la réponse d'un schéma clair annoté.
Question⚓
Q3. (ANA/APP) Les flux à travers la porte, les murs séparant deux appartements, le mur du couloir, le sol et le plafond sont nuls. Justifier.
Solution⚓
A1-Q3.
Comme la température dans les appartements, le couloir est la même, il n'y a pas de transfert d'énergie entre les parois séparant les appartements et le couloir, donc les flux thermiques pour ces parois sont nuls.
En utilisant la formule donnée précédemment, la variation de température est nulle \(\large \Delta\theta=0\), donc \(\large \varphi\) (et aussi \(\large \Phi\)) également.
Question⚓
Q6. (RÉA) Exprimer littéralement, puis calculer la résistance thermique surfacique des murs.
(Réponse : \(R_\mathrm{m}=0,25\ \mathrm{m^2.K.W^{-1}}\) )
Solution⚓
A1-Q6.
\(\large R_\mathrm{m}=R_\mathrm{mur}+\Big(R_\mathrm{si}\Big)_\mathrm{mur}+\Big(R_\mathrm{se}\Big)_\mathrm{mur}\)
\(\large R_\mathrm{m}=\dfrac{e_\mathrm{m}}{\lambda_\mathrm{m}}+\dfrac{1}{h_\mathrm{i}}+\dfrac{1}{h_\mathrm{e}}\)
\(\large R_\mathrm{m}=\dfrac{20\cdot{10}^{-2}}{3,6}+\dfrac{1}{7,0}+\dfrac{1}{20}\)
\(\large \color{blue} R_\mathrm{m}=0,25\ \mathrm{m^2.K.W^{-1}}\)
Question⚓
Q7. (RÉA) Exprimer littéralement, puis calculer la résistance thermique surfacique de la baie vitrée.
(Réponse : \(R_\mathrm{V}=0,20\ \mathrm{m^2.K.W^{-1}}\) )
Question⚓
Q8. (RÉA) Calculer le flux thermique surfacique traversant les murs ; en déduire le flux thermique \(\large \Phi_\mathrm{m}\) traversant cette paroi.
(Réponse : \(\varphi_\mathrm{m}=60\ \mathrm{W.m^{-2}}\) ; \(\Phi_\mathrm{m}=5,9\cdot{10}^2\ \mathrm{W}\) )
Question⚓
Q9. (RÉA) Calculer le flux thermique surfacique traversant la baie vitrée ; en déduire le flux thermique \(\large \mathrm{\Phi_V}\) traversant cette fenêtre.
(Réponse : \(\varphi_\mathrm{V}=75\ \mathrm{W.m^{-2}}\) ; \(\Phi_\mathrm{V}=3,9\cdot{10}^2\ \mathrm{W}\) )
Question⚓
Q10. (RÉA) Calculer la puissance du radiateur électrique permettant d'assurer le maintien de la température intérieure à \(\large 20\ \mathrm{^\circ C}\).
(Réponse : \(P_\mathrm{radiateur}=9,8\cdot{10}^2\ \mathrm{W}\) )
Question⚓
Q11. (RÉA) En déduire l'énergie électrique consommée au cours d'un mois d'hiver de 30 jours.
(Réponse : \(E_\mathrm{consommee}=2,5\cdot{10}^9\ \mathrm{J}=7,1\cdot{10}^2\ \mathrm{kWh}\) )
Question⚓
Q12. Déterminer les températures de surface interne et externe de la baie vitrée. Représenter le profil de températures entre \(\large \theta_\mathrm{i}\) et \(\large \theta_\mathrm{e}\) (sans souci d'échelle).
On donnera les valeurs de températures arrondies à une décimale après la virgule.
(Réponse : \(\theta_\mathrm{{paroi}_{int}}=9,3\ \mathrm{^\circ C}\) ; \(\theta_\mathrm{{paroi}_{ext}}=8,8\ \mathrm{^\circ C}\) )
Question⚓
Q13. (RÉA) Calculer la puissance rayonnée par la paroi extérieure de la baie vitrée ainsi que son émittance.
(Réponse : \(\Phi_\mathrm{ext}=1,8\cdot{10}^{-3}\ \mathrm{W}\) ; \(M_\mathrm{ext}=3,4\cdot{10}^{-4}\ \mathrm{W.m^{-2}}\) )
Question⚓
Q14. (RÉA) Même question pour la paroi intérieure de la baie vitrée
(Réponse : \(\Phi_\mathrm{ext}=2,2\cdot{10}^{-3}\ \mathrm{W}\) ; \(M_\mathrm{ext}=4,2\cdot{10}^{-4}\ \mathrm{W.m^{-2}}\) )