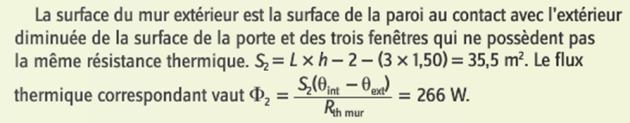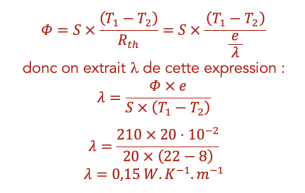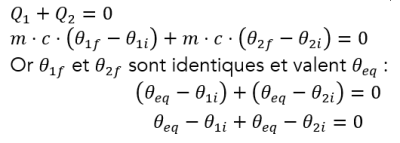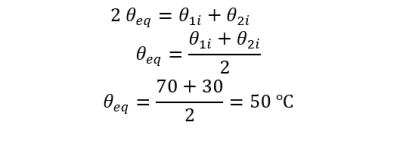Activité n°5 : Exercices d'application 🏋️‍♂️ - [Chap. : Les transferts thermiques]

Pour les exercices de cette activité, vous aurez probablement encore besoin des documents fournis en annexe de l'activité précédente : Cliquer ici pour ouvrir ces documents annexes.

💪 Exercice n°1 : L'eau est froide ⚓

Un ballon d'eau chaude de capacité 200 L contient de l'eau à la température \(\theta_1=60\, \text{°C}\). Quand on prélève de l'eau chaude, elle est remplacée par de l'eau froide à la température \(\theta_2=10\, \text{°C}\). Une fois l'équilibre atteint, la température finale \(\theta_f\) de l'eau dans le ballon a baissé.

On note \(m\) la masse d'eau contenue dans le ballon, et \(m'\) la masse d'eau prélevée. On admet que le ballon est parfaitement isolé.

Rappel : Données pour l'exercice

Capacité thermique massique de l'eau : \(c=4\,180\, \mathrm{J.kg^{-1}.{°C}^{-1}}\)
Masse volumique de l'eau : \(\rho=1\, \mathrm{kg.L^{-1}}\)

Question⚓

Q1. Calculer la température finale \(\theta_f\) de l'eau dans le ballon quand on prélève 20 L d'eau chaude.

Solution ⚓

A2-Q1.

Question⚓

Q2. Quelle masse maximale \(m_{max}\) d'eau peut-on prélever si l'on veut pouvoir disposer d'une eau à 37°C.

Solution ⚓

A2-Q2.

Question⚓

Le ballon est équipé d'une résistance électrique d'appoint de 2 400 W permettant de réchauffer rapidement, en 30 min selon le constructeur, une réserve de 50 L de 20 °C à 40 °C.

Q3. La puissance de la résistance d'appoint est-elle suffisante pour répondre à l'annonce du constructeur ?

Solution ⚓

A2-Q3.

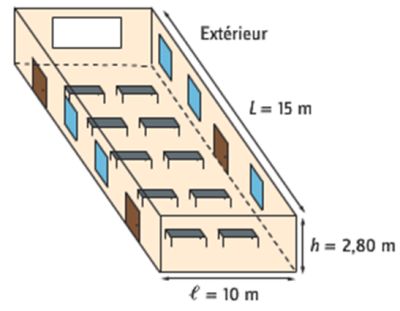
💪 Exercice n°2 : Bilan thermique d'une salle de classe ⚓

Considérons une salle de classe de longueur \(L=15\,m\), de largeur \(\ell=10\,m\) et de hauteur \(h=2,80\,m\).

Sa température est \(\theta_{\text{int}}=20\, \text{°C}\). Trois des quatre murs de la salle sont au contact avec d'autres salles à la même température, le quatrième est au contact de l'extérieur ("mur extérieur"). La température extérieure est \(\theta_{\text{ext}}=5\, \text{°C}\).

Le bilan ne tiendra compte que des pertes par conduction à travers les différentes paroi.

Par ailleurs, la salle de classe possède trois portes identiques de surfaces \(2\, m^{2}\) et cinq fenêtres de surface \(1,5\, m^{2}\). Elle dispose de deux radiateurs de même puissance \(P_1\).

Question⚓

Q4. Calculer les surfaces du plafond et du sol. Que vaut le flux thermique \(\Phi_1\) pour l'ensemble de ces deux parois ?

Solution ⚓

A2-Q4.

Question⚓

Q5. Quelle est la surface du mur en contact avec l'extérieur ? Calculer le flux thermique \(\Phi_2\) pour ce mur.

Solution ⚓

A2-Q5.

Question⚓

Q6. Parmi les cinq fenêtres et les trois portes, lesquels de ces éléments échangent un transfert thermique ? (Expliquer).

Calculer le flux thermique \(\Phi_3\) total associé à ces différents éléments.

Solution ⚓

A2-Q6.

Question⚓

Q7. En déduire le flux thermique \(\Phi_{\text{pertes}}\) perdu par la salle de classe.

Solution ⚓

A2-Q7.

Question⚓

Q8. Quelle doit-être la puissance fournie par un radiateur pour que la température de la classe demeure constante ?

Solution ⚓

A2-Q8.

💪 Exercice n°3 : La matière mystère ⚓

Le flux thermique par conduction à travers un mur de surface \(S=20 \, m^2\) et d'épaisseur \(e=20\, cm\) vaut \(\Phi=210 \, W\). La température intérieure \(\theta_1=22\, \text{°C}\) vaut et la température extérieure \(\theta_2=8\, \text{°C}\).

Complément : Données :

Conductivité thermique \(\mathrm{\left(W.m^{-1}.K^{-1} \right)}\) :

bois de sapin : \(0,15\)
placoplâtre : \(0,46\)
béton plein : \(1,7\)

Question⚓

Q9. Calculer la conductivité thermique \(\lambda\) du matériau avec lequel est fait le mur.

Solution ⚓

A2-Q9.

Question⚓

Q10. Quel est le matériau composant ce mur.

Solution ⚓

A2-Q10. La matériau est donc du bois de sapin.

💪 Exercice n°4 : Isolation d'un chalet savoyard ⚓

Un mur d'un chalet savoyard est composé de l’extérieur vers l'intérieur d'un habillage en bois de sapin d'une épaisseur de 3 cm, d'un mur en béton plein de 18 cm, d'une couche de laine de verre de 10 cm et d'une paroi de placoplâtre (BA13) d'épaisseur 13 mm.

Complément : Données :

Conductivité thermique \(\mathrm{\left(W.m^{-1}.K^{-1} \right)}\) :

bois de sapin : \(0,15\)
laine de verre : \(0,041\)
placoplâtre : \(0,46\)
béton plein : \(1,7\)

Question⚓

Q11. Calculer la résistance thermique \(R_{\text{th}}\), du mur du chalet.

Q12. Quelle devrait être l'épaisseur d'un mur d'un chalet traditionnel uniquement constitué de bois de sapin possédant la même résistance thermique que le mur du chalet de la question précédente ?

Solution ⚓

A2-Q11.

A2-Q12.

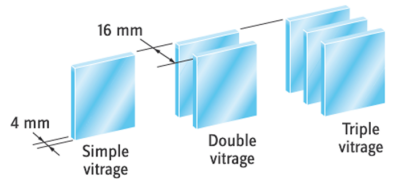
💪 Exercice n°5 : Simple, double et triple vitrage ⚓

On souhaite comparer l'isolation thermique d'un simple vitrage (épaisseur de verre de 4 mm), d'un double vitrage (4-16-4), c'est-à-dire deux plaques de verre de 4 mm séparées par un espace d'air de 16 mm, et d'un triple vitrage (4-16-4-16-4).

Données : Conductivité thermique \(\mathrm{\left(W.m^{-1}.K^{-1} \right)}\) :

air : \(2,5\cdot 10^{-2}\)
verre : \(1,2\)

Question⚓

Q13. Calculer la résistance thermique de chaque vitrage.

Indication :

La résistance thermique d'un matériau composé de plusieurs matériaux est la somme des résistances thermiques de ces matériaux.

Solution ⚓

A2-Q13.

Question⚓

Q14. Calculer le flux thermique par conduction à travers une baie vitrée (en simple vitrage d'épaisseur 4 mm) de surface \(S=8\, m^2\), la température intérieure \(\theta_1=20\, \text{°C}\) étant et la température extérieure \(\theta_2=0\, \text{°C}\) .

Q15. Même question pour une baie vitrée en double vitrage 4-16-4.

Q16. Même question pour une baie vitrée en triple vitrage 4-16-4-16-4.

Solution ⚓

A2-Q14.

Pour le simple vitrage, le flux thermique par conduction vaut :

\[\begin{array}{rcl} {\large\Phi_{\text{simple}}} & = & {\large\frac{S \times \left(\theta_1 -\theta_2 \right)}{R_{\text{th simple}}}} \\ & = & {\large\frac{8 \times \left(20 -0 \right)}{3,3 \cdot 10^{-3}}} \\ & = & {\large\mathbf{4,8 \cdot 10^{4} \, W=48 \, kW}} \\ \end{array}\]

A2-Q15. Pour le double vitrage, le flux thermique par conduction vaut :

\[\begin{array}{rcl} {\large\Phi_{\text{double}}} & = & {\large\frac{S \times \left(\theta_1 -\theta_2 \right)}{R_{\text{th double}}}} \\ & = & {\large\frac{8 \times \left(20 -0 \right)}{0,65}} \\ & = & {\large\mathbf{2,5 \cdot 10^{2} \, W}} \\ \end{array}\]

A2-Q16. Pour le triple vitrage, le flux thermique par conduction vaut :

\[\begin{array}{rcl} {\large\Phi_{\text{triple}}} & = & {\large\frac{S \times \left(\theta_1 -\theta_2 \right)}{R_{\text{th triple}}}} \\ & = & {\large\frac{8 \times \left(20 -0 \right)}{1,3}} \\ & = & {\large\mathbf{1,2 \cdot 10^{2} \, W}} \\ \end{array}\]

Question⚓

Q17. Lequel des trois vitrages offre la meilleure isolation thermique ? Pourquoi ?

Solution ⚓

A2-Q17.

Le vitrage procurant la meilleure isolation thermique est celui limitant au mieux les transferts thermiques (qualifiées ici de pertes thermiques) : c'est donc le triple vitrage ! Le flux thermique par conduction est divisé par 400 par rapport au simple vitrage.

💪 Exercice n°6 : Étude expérimentale de la conduction thermique ⚓

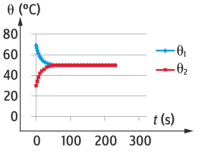
Dans une enceinte calorifugée (pas de pertes d'énergie), on place au contact deux blocs de métal de mêmes masses portés initialement par bain-marie aux températures initiales \(\theta_{\text{1i}}=70\, \text{°C}\) et \(\theta_{\text{2i}}=30\, \text{°C}\) .

Chaque bloc dispose d'un petit trou dans lequel on place une sonde thermométrique et on relève la température des deux blocs toutes les 10 s grâce à un système d'enregistrement informatisé.

On obtient les courbes ci-contre.

Question⚓

Q18. Les métaux sont-ils de bons ou de mauvais conducteurs de la chaleur ?

Solution ⚓

A2-Q18. Les métaux sont de bons conducteurs de la chaleur.

Question⚓

Q19. Dans quel sens se font les transferts thermiques entre les deux blocs ? Pour quelle raison a-t-on calorifugé l'enceinte ?

Solution ⚓

A2-Q19.

Le transfert thermique se fait du chaud vers le froid

On a calorifugé l'enceinte, pour avoir une bonne précision de mesure en limitant au maximum les pertes d'énergie vers l'extérieur (pour être plus précis il faudrait comptabiliser l'augmentation de température de l'air intérieur).

Question⚓

Q20. Quel est le mode de transfert thermique entre les deux blocs ?

Solution ⚓

A2-Q20.

Le transfert thermique s'effectue par conduction (agitation des atomes transmise de proche en proche mais sans déplacement de la matière).

Question⚓

Q21. Comment évolue la température \(\theta_{\text{1}}\) du bloc de métal 1 ?

Solution ⚓

A2-Q21.

Le bloc 1 voit sa température diminuer puis stagner à une valeur.

Question⚓

Q22. Comment évolue la température \(\theta_{\text{2}}\) du bloc de métal 2 ?

Solution ⚓

A2-Q22.

Le bloc 2 voit sa température augmenter puis stagner à une valeur.

Question⚓

Q23. Pourquoi les deux températures tendent-elles vers une même valeur ? Que est cette valeur ?

Solution ⚓

A2-Q23.

Ils tendent vers une température commune car au bout d'un certain temps il n'y a plus d'échange thermique. On lit graphiquement que l'on a une température de 50 °C.

On rappelle que le transfert thermique reçu par un corps est :

\[\begin{array}{rcl} {\large Q=m\cdot c\cdot \left ( \theta_{\text{f}} - \theta_{\text{i}} \right ) \text{ avec :}} & & {\large Q\text{ : l'énergie transférée en J ; } }\\ & & {\large m\text{ : la masse du corps en kg ;} } \\ & & {\large c\text{ : la capacité thermique massique du corps, en } \mathrm{ J.kg^{-1}.\text{°C}^{-1}} } \\ & & {\large \theta_{\text{i}} \text{ et } \theta_{\text{f}}\text{ : les températures initiale et finale en °C.} } \\ \end{array}\]

Question⚓

Pour les applications numériques, on prendra deux blocs de même masse \(m=100 \, g\) et de capacité thermique massique \(c=9,0 \cdot 10^2 \: \mathrm{J.kg^{-1}.\text{°C}^{-1}}\).

Q24. Calculer le transfert thermique reçu par le bloc 2 au cours de la transformation.

Q25. Même question pour le bloc 1. Que signifie le fait que le transfert thermique reçu par le bloc 1 soit négatif ?

Solution ⚓

A2-Q24.

\({\large Q_2=m\cdot c\cdot \left ( \theta_{\text{2f}} - \theta_{\text{2i}} \right ) = 0,100 \times 9,0\cdot 10^{2} \times \left ( 50 - 30 \right ) \,\mathbf{=1,8 \, kJ}}\)

A2-Q25.

\({\large Q_1=m\cdot c\cdot \left ( \theta_{\text{1f}} - \theta_{\text{1i}} \right ) = 0,100 \times 9,0\cdot 10^{2} \times \left ( 50 - 70 \right ) \,\mathbf{=-1,8 \, kJ}}\)

Le bloc 1 perd donc de l'énergie, c'est pour cela que le transfert thermique est négatif.

Question⚓

Q26. Montrer que la température d'équilibre théorique entre les deux blocs est : \({\Large \theta_{\text{eq}} = \frac{\theta_{\text{1i}}-\theta_{\text{2i}}}{2} }\)

Comparer à la valeur obtenue expérimentalement.

Solution ⚓

A2-Q26.

Comme il n'y a pas de pertes, toutes l'énergie cédée par le bloc 1 est intégralement reçue par le bloc 2, donc on a :

On trouve la même valeur que la valeur expérimentale.

Question⚓

Q27. Estimer à l'aide de la courbe le temps au bout duquel l'équilibre thermique est atteint.

Solution ⚓

A2-Q27.

On lit graphiquement que l'équilibre thermique semble atteint pour une durée de \(50\ \mathrm{s}\) environ.