🔊 Nature du son et propagation⚓
Complément : 📄Document n°1 : Qu’est-ce qu’une onde mécanique ?
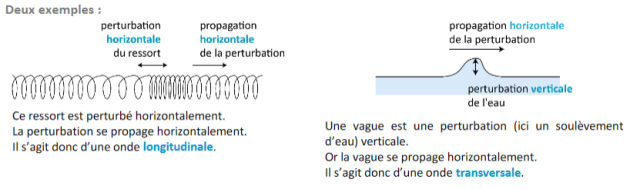
Une onde est la propagation d’une perturbation produisant sur son passage une variation réversible des propriétés physiques locales du milieu. Elle se déplace avec une vitesse déterminée qui dépend des caractéristiques du milieu de propagation. Une onde transporte de l’énergie sans transporter de matière.
Une onde peut être transversale ou longitudinale.
Regarder la vidéo ci-dessous :
Complément : 📄Document n°2 : Onde sonore
Une source sonore crée une surpression dans le milieu, appelée pression acoustique. Cette surpression se propage de proche en proche et constitue l’onde sonore.
Modèle microscopique de la propagation d’une onde sonore dans un gaz
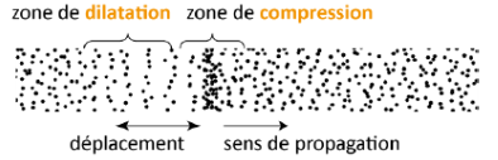
L’onde sonore est une onde mécanique longitudinale. La perturbation est une variation de la pression, appelée pression acoustique.
Complément : 📄Document n°3
Comme toute les ondes mécaniques, l’onde sonore ne peut exister que dans un milieu matériel. La célérité des ondes sonores dépend de leur milieu de propagation :
Milieu de propagation | Caoutchouc souple | Air sec | Vapeur d’eau | Eau | Béton | Acier, verre |
|---|---|---|---|---|---|---|
c (en \(\mathrm{m\cdot s^{-1}}\)) | 70 | 340 | 402 | 1 400 | 3 000 | 5 000 |
Voir l’animation suivante : https://dgxy.link/animation_son_2 
Question⚓
Q3. Quelle grandeur physique se propage avec une onde sonore ?
Solution⚓
Q3.
La grandeur physique qui se propage avec une onde sonore est la pression. Les ondes sonores sont des variations de pression qui se déplacent à travers un milieu (comme l'air, l'eau ou les solides) en faisant vibrer les particules de ce milieu. Ces variations de pression sont perçues par nos oreilles comme des sons.
Question⚓
Q4. Quelle est la perturbation qui se propage ?
Question⚓
Q6. Comparer les vitesses de propagation dans les différents matériaux.
Solution⚓
Q6.
Les vitesses de propagation du son varient considérablement en fonction des matériaux. Voici quelques exemples tirés des documents :
Caoutchouc souple : 70 m/s
Air sec : 340 m/s
Vapeur d'eau : 402 m/s
Eau : 1 400 m/s
Béton : 3 000 m/s
Acier, verre : 5 000 m/s
Comme on peut le constater, le son se propage beaucoup plus rapidement dans des matériaux denses comme l'acier et le verre, par rapport à des matériaux moins denses comme l'air ou le caoutchouc souple. Cela est dû à la manière dont les particules dans ces matériaux interagissent et transmettent l'énergie sonore.
Question⚓
Q7. Proposer une explication.
Solution⚓
Q7.
Pour expliquer pourquoi les vitesses de propagation du son varient dans différents matériaux, il est important de comprendre les propriétés physiques de ces matériaux. La célérité du son dépend de la densité et de l'élasticité du milieu de propagation.
Dans les matériaux plus denses comme l'acier ou le verre, les particules sont plus proches les unes des autres, ce qui permet une transmission plus rapide des vibrations sonores. En revanche, dans des matériaux moins denses comme l'air ou le caoutchouc souple, les particules sont plus éloignées, ce qui ralentit la propagation du son.
De plus, l'élasticité du matériau joue un rôle crucial. Les matériaux plus élastiques, comme l'acier, permettent aux ondes sonores de se propager plus rapidement car ils peuvent revenir rapidement à leur état initial après avoir été déformés par la pression acoustique.
📝 Deux types de périodicité⚓
👁️ 1ère partie : Reconnaître les deux périodicités⚓
Complément : 📄Document n°4
Une voiture circule sur une route au milieu de laquelle sont tracés des pointillés. Ils sont ainsi disposés : un tiret de 3m, un espace de 10m, un tiret de 3m, etc.
Afin de signaler qu'elle va tourner à gauche prochainement, la voiture allume son clignotant, lequel s'allume 2 fois toutes les 3 secondes.
👁️ 2ème partie : Périodicité(s) dans le cas d'une onde⚓
Attention :
Liens d'accès :
SimulaSON : https://dgxy.link/USpuK
 ;
;
SimulaCORDE :https://dgxy.link/YKETN
 .
.
🎯 Objectif
Distinguer les représentations des perturbations au cours du temps ou dans l'espace et savoir les exploiter.
💻 Simulation :
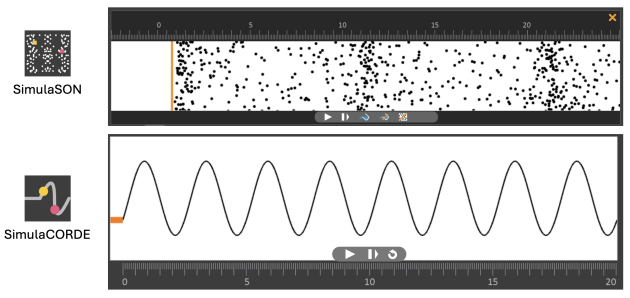
Dans le logiciel simulaSON, simuler une onde sonore (elle est sinusoïdale par souci de simplification) de fréquence \(1,5\ \mathrm{Hz}\).
Observer la représentation microscopique dans le tuyau sonore simulé.
Question⚓
Q11. Dans la situation réelle, quelle est la grandeur physique qui caractérise le milieu de propagation et varie lors de la propagation d'un son ?
Question⚓
Q12. Représenter ci-dessous la variation spatiale de cette grandeur dans le tuyau sonore à un instant donné (échelle des ordonnées arbitraire).

Question⚓
Q13. Dans le repère ci-dessous, prévoir la variation temporelle de cette grandeur à un endroit donné pour un capteur qui serait placé dans le milieu (on placera des graduations sur l'axe des abscisses) :

💻 Simulation :
Vérifier la réponse précédente à l'aide de la fenêtre « évolution temporelle de la pression acoustique » en plaçant le capteur 1 dans le milieu.
Ouvrir le logiciel SimulaCORDE et régler les paramètres afin d'obtenir une onde périodique sinusoïdale de fréquence \(1,5\ \mathrm{Hz}\). Afficher la représentation spatiale de la hauteur de la corde ainsi que la représentation temporelle de la hauteur en un point.
Question⚓
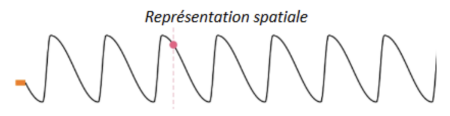
Q14. On va simuler une onde périodique non sinusoïdale. La représentation spatiale de la grandeur aura l'allure représentée à gauche ci-dessous. Sur le graphique de droite, représenter l'allure des variations temporelles de la hauteur en un point de la corde, par exemple celui repéré par le disque rose :

💻 Simulation :
Vérifier votre réponse précédente en utilisant le curseur « Déformation ».
Question⚓
Q15. Pour une onde, la période spatiale est appelée « longueur d'onde » et est généralement notée \(\lambda\).
Sur tous les quatre graphiques tracés dans cette partie, faire apparaître soit la grandeur « période temporell » \(T\), soit la grandeur « longueur d'onde » \(\lambda\).
👁️ 3ème partie : Relation entre période, fréquence et longueur d'onde⚓
On considère la situation représentée sur le graphique de gauche à la fin de la partie précédente.
Question⚓
Q16. On note \(A\) la position du capteur à l'instant où l'image est réalisée. On note \(B\) le point immédiatement à gauche qui est dans le même état vibratoire que \(A\). Représenter \(A\) et \(B\) sur la figure. Que représente la distance \(AB\) pour l'onde étudiée ?