Activité n°4 : Le pouvoir de combustion

Titre de l'activité : Activité n°4 : Le pouvoir de combustion - [Chap. Les combustions]

Durée : 2h

Compétences

ANA - Exploiter ses connaissances, les informations extraites ou les résultats obtenus
APP - Rechercher et extraire l'information
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
APP - Mobiliser les connaissances en rapport avec le problème
RÉA - Suivre une procédure, un mode opératoire
RÉA - Mesurer
RÉA - Équilibrer une équation de réaction
RÉA - Calculer, utiliser une formule
RCO - Restituer des connaissances

Notions

Évaluer, à l’aide d’une formule fournie, l’énergie libérée lors d’une combustion à pression constante (variation d’enthalpie).
Définir et comparer les pouvoirs calorifiques de quelques carburants.
Vocabulaire et définitions : Aspects énergétiques associés à la combustion ; ordres de grandeurs
Vocabulaire et définitions : Pouvoir calorifique d’un combustible

L’objectif de cette activité est de calculer l'économie réalisée lors du remplacement d'une chaudière ancienne par une chaudière à condensation.

📄 Introduction et documents ⚓

Le fonctionnement d'une chaudière à condensation reprend le même principe que celui qu'une chaudière traditionnelle mais il permet, en plus, de tirer profit de toute l'énergie produite lors de la combustion.

Complément : Document n°1 : Principe de la condensation dans les chaudières

Schéma du principe de fonctionnement d'une chaudière à condensation :

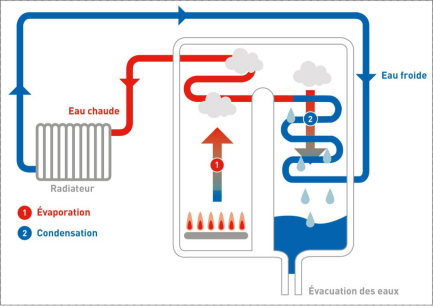
Dans une chaudière classique, le circuit d'eau du chauffage est réchauffé grâce à la chaleur libérée par la combustion (du gaz naturel pour une chaudière à gaz par exemple).

Une chaudière à condensation tire profit de l'énergie contenue dans les fumées de combustion. Ces fumées, dont la température peut atteindre 200 °C (dans le cas du gaz naturel), contiennent de la vapeur d'eau. Lorsque l'on refroidit les fumées, la vapeur d'eau se condense en libérant de la chaleur, que l'eau de retour du circuit de chauffage absorbe pour se réchauffer.

L'évacuation de l'eau libérée lors de la condensation (les condensats) se fait par le réseau des eaux usées.

Complément : Document n°2 : Quelques données

L’eau :

Enthalpie massique de vaporisation : $L_{vap}=2,257\ \mathrm{MJ\cdot kg^{-1}}$
$\theta_\textit{éb}=100 \mathrm{^\circ C}$ sous une pression $p=1\ atm={10}^{13}\ \mathrm{hPa}$
Capacité thermique massique de l'eau à l'état gazeux : $c_{eau,g}=1\ 410\ \mathrm{J\cdot kg^{-1}\cdot K^{-1}}$
Capacité thermique massique de l'eau à l'état liquide : $c_{eau,\ell}\ =\ 4\ 185\ \mathrm{J\cdot kg^{-1}\cdot K^{-1}}$

Méthane :

Formule chimique brute : $\ce{CH4}$
Pouvoir combustible inférieur : $PCI=50,1\ \mathrm{MJ\cdot kg^{-1}}$

Dioxyde de carbone :

Capacité thermique massique du dioxyde de carbone dans l'état gazeux : $c_{\ce{CO2}}=650\ \mathrm{J\cdot kg^{-1}\cdot K^{-1}}$

Caractéristiques des chaudières :

Température de sortie des fumées
- Chaudière ancienne : $T_\textit{fumées}=200\ \mathrm{^\circ C}$ environ ;
- Chaudière à condensation : $T_\textit{fumées}=50\ \mathrm{^\circ C}$ environ.
Température d'évacuation des condensats (chaudière à condensation)
- $T_\textit{condensats}=20\ \mathrm{^\circ C}$.

Masse molaire atomiques de certains éléments :

$M_{\ce{H}}=1,0\ \mathrm{g\cdot mol^{-1}}$
$M_{\ce{C}}=12,0\ \mathrm{g\cdot mol^{-1}}$
$M_{\ce{O}}=16,0\ \mathrm{g\cdot mol^{-1}}$
$M_{\ce{N}}=14,0\ \mathrm{g\cdot mol^{-1}}$

Définition : Document n°3 : Rappel sur les échanges d’énergie thermique

Lors d’une variation de température $\Delta\theta$ d’un corps de masse $m$, l’énergie $Q$ du transfert thermique s’exprime par :

\[\begin{array}{lcl} {\fcolorbox{red}{white}{$ {\Large \color{red}\ \ \ \mathbf{ Q = m \cdot c \cdot \Delta \theta } \ \ \ } $}} & \textsf{ avec :} & \begin{array}{|lcl} {\large\ \mathbf{Q} } & \textsf{:} & { \textsf{énergie du transfert thermique } \left(\ \mathrm J \ \right) }\\ {\large\ \mathbf{m} } & \textsf{:} & {\textsf{masse } \left(\ \mathrm{kg} \ \right) } \\ {\large\ \mathbf{c} } & \textsf{:} & {\textsf{capacité thermique massique } \left(\ \mathrm{J\cdot kg^{-1}\cdot ^\circ C^{-1} } \ \right) } \\ {\large\ \mathbf{\Delta \theta} } & \textsf{:} & \textsf{variation de température } \left(\ \mathrm{^\circ C^{-1}} \textsf{ ou } \mathrm{K^{-1} } \ \right) \\ & & \textsf{tel que } \large \Delta\theta=\theta_f-\theta_i \end{array} \end{array} \]

La valeur du transfert thermique est positive si le corps reçoit de la chaleur et négative s’il en donne.

On parle alors de variation d’énergie interne, que l’on a vue dans le chapitre n°9 de 1ère année.

L’énergie nécessaire au changement d’état d’un corps de masse $m$ est :

\[\begin{array}{lcl} {\fcolorbox{red}{white}{$ {\Large \color{red}\ \ \ \mathbf{ Q = m \cdot L } \ \ \ } $}} & \textsf{ avec :} & \begin{array}{|lcl} {\large\ \mathbf{Q} } & \textsf{:} & { \textsf{énergie du transfert thermique } \left(\ \mathrm J \ \right) }\\ {\large\ \mathbf{m} } & \textsf{:} & {\textsf{masse } \left(\ \mathrm{kg} \ \right) } \\ {\large\ \mathbf{L} } & \textsf{:} & {\textsf{chaleur latente de changement d’état } \left(\ \mathrm{J\cdot kg^{-1}} \ \right) } \end{array} \end{array} \]

L’enthalpie massique de changement d’état, appelé également chaleur latente de changement d’état, dépend du changement d’état, et du sens de ce changement d’état.

Ainsi, $L_\textit{fusion}=-L_\textit{solidification}$. Pour une solidification, peut utilisera $L_\textit{solidification}=-L_\textit{fusion}$.

Complément : Document n°4 : Le pouvoir calorifique

On appelle pouvoir calorifique inférieur d’un combustible, l’énergie libérée par la combustion complète d’un kilogramme de ce combustible. Les réactifs et les produits sont gazeux. On le note le plus souvent PCI, il s’exprime généralement en $\mathrm{kJ\cdot kg^{-1}}$.
On peut alors calculer l’énergie totale libérée (en $\mathrm J$) par une masse $m_\textit{combustible}$ (en $\mathrm{kg}$) de combustible, dans le cas où toutes les espèces chimiques sont gazeuses : $\mathbf{Q_\textit{comb}=m_\textit{combustible}\times PCI}$
On appelle pouvoir calorifique supérieur d’un combustible, l’énergie libérée par la combustion complète d’un kilogramme de ce combustible en comptabilisant l’énergie gagnée lors de la liquéfaction (condensation dans le langage courant) des produits gazeux. On le note le plus souvent PCS, il s’exprime généralement en en $\mathrm{kJ\cdot kg^{-1}}$.
On peut alors calculer l’énergie totale libérée (en $\mathrm J$) par une masse $m_\textit{combustible}$ (en $\mathrm{kg}$) de combustible, tenant compte de l’énergie gagnée par la liquéfaction des gaz produits : $\mathbf{Q_\textit{comb}=m_\textit{combustible}\times PCS}$
Si on note $Q_\textit{récup}$ l’énergie récupérée par la liquéfaction des gaz produits, alors on a : $PCS=Q_\textit{récup}+PCI$

💧 L’intérêt d’une chaudière à condensation ⚓

Une documentation proposée par un installateur affirme que le remplacement d'une chaudière « ancienne » par une chaudière à condensation permet une économie de 20 à 35 % sur la consommation.

À vous de le vérifier en répondant aux questions ci-dessous ...

Attention :

Dans tout le problème, on considérera la combustion de $1,00\ \mathrm{kg}$ de gaz naturel (méthane, de formule chimique $\ce{CH4}$).

Question⚓

Q1. Écrire l'équation de combustion complète du méthane dans le dioxygène de l'air.

Aide : Les coefficients stœchiométriques sont ajustés de façon à respecter la conservation des éléments chimiques au cours de la transformation.

Solution ⚓

Q1.

La combustion complète d'un hydrocarbure dans le dioxygène de l'air produit du dioxyde de carbone et de l'eau, d'où l'équation : $CH_4+2\ O_2\ \longrightarrow\ CO_2+2\ H_2O$

Question⚓

Q2. Calculer la quantité de matière de méthane correspondant à la masse $m_{\ce{CH4}}=1,00\ \mathrm{kg}$.

Aide : Pensez à comment est définie la masse molaire moléculaire. Pensez également aux chiffres significatifs.

Solution ⚓

Q2.

La quantité de matière de méthane $n_{\ce{CH4}}$ correspondant à la masse de méthane $m_{\ce{CH4}}$ s'exprime par :

$n_{\ce{CH4}}=\dfrac{m_{\ce{CH4}}}{M_{\ce{CH4}}} $avec $M_{\ce{CH4}}=M_{\ce{C}}+4\times M_{\ce{H}}=12,0+4\times1,0=16,0\ \mathrm{g \cdot mol^{-1}}$

Pour $1,00\ \mathrm{kg}$ de méthane : $n_{\ce{CH4}}=\dfrac{1,0\cdot{10}^3}{16,0}=62,5\ \mathrm{mol}$

Question⚓

Q3. Calculer les masses molaires moléculaires des gaz produits ($\ce{CO2}$ et $\ce{H2O}$).

Aide : Pensez à comment est définie la masse molaire moléculaire. Pensez également aux chiffres significatifs.

Solution ⚓

Q3.

$M_{\ce{CO2}}=M_C+2\times M_O=12,0+2\times16,0=44,0\ \mathrm{g \cdot mol^{-1}}$

$M_{\ce{H2O}}=2\times M_H+M_O=2\times1,0+16,0=18,0\ \mathrm{g \cdot mol^{-1}}$

Question⚓

Q4. À l'aide d'un tableau d’avancement, déterminer les quantités de matière des gaz produits lors de la combustion de $1,00\ \mathrm{kg}$ de méthane.

Aide : Pour le tableau d’avancement, pensez aux coefficients stœchiométriques. Dans l’air, le dioxygène est en excès. On doit avoir $\left({\ce{CO2}}\right)_f=62,5\ \mathrm{mol}$.

Question⚓

Q5. Déduire des deux calculs précédents les masses des gaz produits lors de la combustion.

Aide : Pensez aux chiffres significatifs.

Solution ⚓

Q5.

$\left(m_{\ce{CO2}}\right)_f=\left(n_{\ce{CO2}}\right)_f\times M_{\ce{CO2}}=62,5\times44,0=2,75\cdot{10}^3\ g=2,75\ \mathrm{kg}$

$\left(m_{\ce{H2O}}\right)_f=\left(n_{\ce{H2O}}\right)_f\times M_{\ce{H2O}}=125\times18,0=2,25\cdot{10}^3\ g=2,25\ \mathrm{kg}$

Question⚓

Q6. Calculer l’énergie fournie par la combustion dans le cas d’une chaudière standard, c’est-à-dire sans liquéfaction des gaz.

Aide : Il faut utiliser le PCI.

Solution ⚓

Q6.

Si on ne procède pas au refroidissement des gaz, et si on considère une combustion parfaite et complète du méthane, on peut récupérer une chaleur $Q_\textit{comb}$ qui vaut :

$Q_\textit{comb}=m_{\ce{CH4}}\times PCI=1,00\times50,1\times{10}^6=50,1\cdot{10}^6\ \mathrm{J}$

Question⚓

Q7. Calculer les énergies récupérées lors des transformations subies par les espèces chimiques présentes dans les fumées lorsqu'on les refroidit :

$\ce{CO2}$ : refroidissement de $200\ \mathrm{^\circ C}$ à $55\ \mathrm{^\circ C}$ sans changement d'état ;
$\ce{H2O}$ : refroidissement de $200\ \mathrm{^\circ C}$ à $100\ \mathrm{^\circ C}$ sans changement d'état ;
$\ce{H2O}$ : changement d'état gaz-liquide à $100\ \mathrm{^\circ C}$ ;

$\ce{H2O}$ : refroidissement de $100\ \mathrm{^\circ C}$ à $20\ \mathrm{^\circ C}$ sans changement d'état.

Aide : Il faut utiliser les formules du Doc.3, en faisant attention aux chiffres significatifs des données fournies par le Doc.2.

Les valeurs obtenues sont négatives, soit parce qu'il s'agit d'un refroidissement (entraînant une diminution de l'énergie interne du corps) soit parce qu'il s'agit d'un changement d'état d'un état moins dense (gaz) vers un état plus dense (liquide).

Solution ⚓

Q7.

La variation d’énergie du dioxyde de carbone qui passe $\theta_i=200\ \mathrm{^\circ C}$ à $\theta_f=55\ \mathrm{^\circ C}$ sans changement d’état vaut :
$Q_1=m_{\ce{CO2}}\times c_{\ce{CO2}}\times\left(\theta_f-\theta_i\ \right)=2,75\times650\times\left(55-200\right)=-2,59\cdot{10}^5\ J$
La variation d’énergie de l’eau gazeuse qui passe $\theta_i=200\ \mathrm{^\circ C}$ à $\theta_f=55\ \mathrm{^\circ C}$ sans changement d’état vaut :
$Q_2=m_{\ce{H2O}}\times c_{eau,\ g}\times\left(\theta_f-\theta_i\ \right)=2,25\times1410\times\left(100-200\right)=-3,17\cdot{10}^5\ J$
La variation d’énergie de l’eau gazeuse qui change d’état à température constante de $100\ \mathrm{^\circ C}$ vaut :
$Q_3=m_{\ce{H2O}}\times\left(-L_{vap}\right)=2,25\times2,257\cdot{10}^6=-5,08\cdot{10}^6\ J$
La variation d’énergie de l’eau liquide qui passe $\theta_i=100\ \mathrm{^\circ C}$ à $\theta_f=20\ \mathrm{^\circ C}$ sans changement d’état vaut :
$Q_2=m_{\ce{H2O}}\times c_{eau,\ \ell}\times\left(\theta_f-\theta_i\ \right)=2,25\times4185\times\left(20-100\right)=-7,5\cdot{10}^5\ J$

Question⚓

Q8. La somme des énergies récupérées représente-t-elle effectivement l'économie supposée d'après l'installateur ?

Si non, l'écart est-il dû à un mensonge de l'installateur ou à une étude incomplète ? Justifier votre réponse.

Aide : Il faut ajouter les énergies calculées précédemment. Puis vérifier le % d’économie du fabriquant. Vous devriez trouver $\approx13\ \%$. Il faudra s’interroger sur la différence obtenue en se demandant tout ce qui n’a pas été considéré dans l’étude.

Solution ⚓

Q8.

Le refroidissement des gaz se traduit par une variation totale d'énergie $Q_\textit{tot,récup}$ valant :

$Q_\textit{tot,récup}=Q_1+Q_2+Q_3+Q_4=-2,59\cdot{10}^5-3,17\cdot{10}^5-5,08\cdot{10}^6-7,5\cdot{10}^5=-6,41\cdot{10}^6\ \mathrm{J}$

Le calcul du rapport entre l'énergie récupérée au refroidissement et l'énergie due à la combustion montre que l'énergie récupérée représente seulement 13 % de l'énergie produite par la combustion, ce qui ne correspond pas à l'affirmation faite par l'installateur. $\dfrac{Q_\textit{tot,récup}}{Q_\textit{comb}}=\dfrac{6,41\cdot{10}^6}{50,1\cdot{10}^6}=0,128=12,8 \%$

Cependant, on ne peut affirmer qu'il ment car l'étude menée est incomplète.

Lors de la combustion, le diazote, qui représente 80 % en volume de l'air aspiré, subit le même refroidissement que le dioxyde de carbone. Si on tient compte de l'énergie restituée par le diazote, l'énergie totale récupérée représente alors 17 % de la chaleur produite par la combustion.
La prise en compte du diazote ne suffit pas à expliquer l'écart observé. On peut toutefois prendre en compte le fait que dans une chaudière ancienne, la combustion du méthane a un rendement plus faible que dans une chaudière à condensation récente. Une recherche documentaire permet de trouver des rendements de combustion de l'ordre de 90 % pour une chaudière ancienne alors qu'il atteint aisément 100 % dans une chaudière moderne. La prise en compte de cet aspect permet déjà d'atteindre une économie de 20 %. Il faudrait également considérer les pertes par les parois de la cuve de la chaudière : dans une chaudière ancienne, elles sont plus importantes que dans une chaudière moderne.