📢 Différents sons⚓
Expérience n°1
En utilisant un ordinateur et un microphone 🎤 (ou micro-casque), enregistrer le son d’un diapason avec Audacity. Zoomer sur le signal enregistrer pour retrouver le type de signal ci-dessus.
Enregistrer ensuite votre voix pour une note de musique 🎵 constante (même si fausse 😉). Zoomer également sur le signal et identifier une période.
🔊 Un son complexe, qu'est-ce que c’est ?⚓
Méthode :
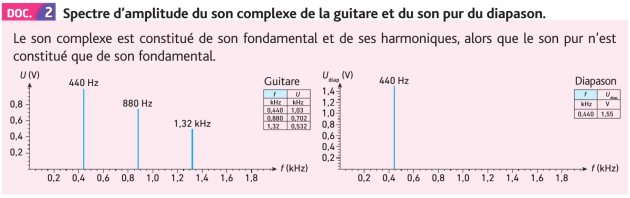
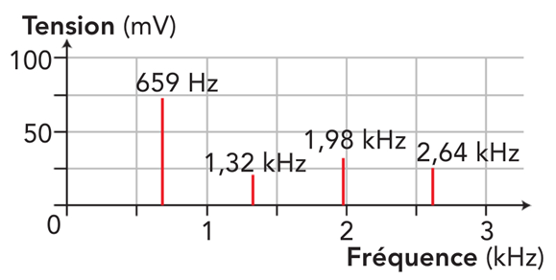
Pour étudier des sons, on trace le spectre d’une onde acoustique.
Définition : 📌 Définition du spectre d'une onde acoustique
On montre en mathématiques que tout signal peut être décomposé en une somme de signaux sinusoïdaux de fréquences différentes. Chacun de ces signaux sinusoïdaux est appelé un harmonique du signal.
Le spectre d'une onde acoustique est la représentation de l'amplitude de chaque harmonique dont l'onde est composée, en fonction de sa fréquence.
L'opération mathématique permettant de passer de la représentation temporelle d'un signal à son spectre s'appelle la transformée de Fourier.
Question⚓
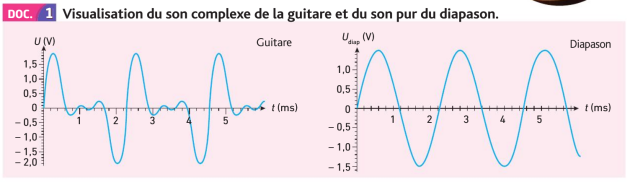
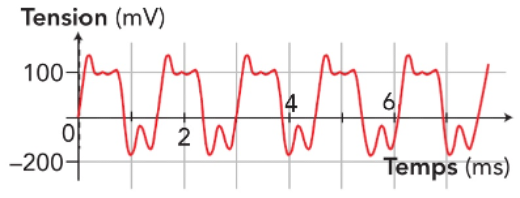
Q2. Vérifier que les deux sons ont la même période \(T\), et en déduire leur fréquence.
Solution⚓
Q2.
Pour le signal de la guitare, on a \(2\times T=4,6\ \mathrm{ms}\) donc \(T=\dfrac{4,6}{2}=2,3\ \mathrm{ms}\), donc \(f=\dfrac{1}{T}=\dfrac{1}{2,3 \cdot 10^{-3}}=4,3 \cdot 10^2 \ \mathrm{Hz}\), soit \(f\approx430\ \mathrm{Hz}\).
Pour le signal du diapason, on a \(2\times T=4,65\ \mathrm{ms}\) donc \(T=\dfrac{4,65}{2}=2,33\ \mathrm{ms}\), donc \(f=\dfrac{1}{T}=\dfrac{1}{2,33 \cdot 10^{-3}}=4,3 \cdot 10^2 \ \mathrm{Hz}\), soit \(f\approx430\ \mathrm{Hz}\).
Question⚓
Q7. Conclure en expliquant comment reconnaitre un son pur et un son complexe grâce à leur spectre d’amplitude.
🏋🏻 Application⚓
🗯️ Pour aller plus loin⚓
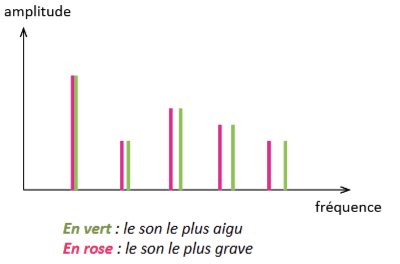
Définition : 📌 La hauteur d'un son
La hauteur du son est une propriété sensorielle. Un son « haut » est un son perçu comme aigu, un son « bas »est perçu comme grave.
En physique, la hauteur du son est modélisée par la fréquence fondamentale de l'onde sonore correspondante. Plus cette fréquence est élevée, plus le son est perçu comme aigu.
Représentations temporelles de deux sons de hauteurs différentes :

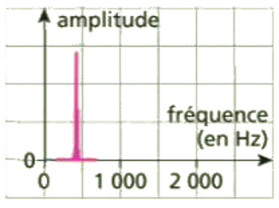
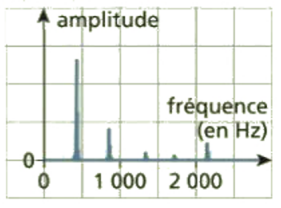
Spectres de deux sons de hauteurs différentes :
Définition : 📌 Le timbre d'un son
Le timbre est une propriété sensorielle du son. Il distingue deux sons musicaux émis par deux instruments différents jouant la même note de musique.
Deux sons de même hauteur mais de timbres différents :
ont des représentations temporelles de même fréquence mais de motifs différents ;
ont des spectres de même fréquence fondamentale mais avec des harmoniques d'amplitudes différentes.
Représentations temporelles de deux sons de même hauteur mais de timbres différents :
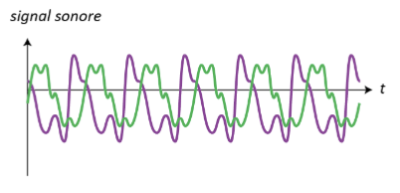
Ces deux sons ont la même période, donc la même fréquence, mais pas le même motif :ils diffèrent par leur timbre.
Spectres de deux sons de même hauteur mais de timbres différents :
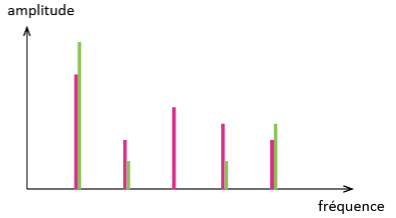
Ces deux sons ont un fondamental de même fréquence mais des harmoniques d'amplitudes différentes : ils diffèrent par leur timbre.