Activité n°6 : Exercices - [Chap. Les ondes sonores]

Titre de l'activité : Activité n°6 : Exercices - [Chap. Les ondes sonores]

Durée : 1h

Compétences

ANA - Exploiter ses connaissances, les informations extraites ou les résultats obtenus
APP - Rechercher et extraire l'information
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
APP - Mobiliser les connaissances en rapport avec le problème
COM - Rendre compte à l'écrit ou à l'oral

Notions

Caractériser une onde mécanique par les grandeurs physiques associées : vitesse, amplitude de la déformation, période, fréquence, longueur d'onde.
Associer la propagation d'une onde mécanique à un transfert d'énergie sans transport de matière dans un milieu matériel.
Distinguer une onde longitudinale d'une onde transversale.
Associer la propagation d'une onde mécanique à un transfert d'énergie sans transport de matière dans un milieu matériel.
Donner et comparer l'ordre de grandeur et de la vitesse de propagation d'une onde acoustique dans quelques milieux : air, liquide, matériaux du domaine professionnel.
Connaître et exploiter la relation entre la longueur d'onde, la fréquence et la célérité d'une onde acoustique.
Analyser expérimentalement un son simple, un son complexe, un bruit, mettre en évidence sa composition spectrale.
Définir et mesurer quelques grandeurs physiques associées à une onde acoustique : pression acoustique, amplitude, période, fréquence, célérité.

💪 Exercice n°1 : À quel niveau se trouve l'eau ?⚓

Dans une installation industrielle, un capteur à ultrasons est à 1,00 mètre au-dessus du fond d'une cuve d'eau.

Dans l'entrepôt, la température est maintenue à \(20\ \mathrm{^\circ C}\). Ce capteur à ultrasons est composé d'un émetteur de salves d'ultrasons (E) et d'un récepteur (R) d'ultrasons. Il est placé au-dessus de la surface de l'eau. Les mesures se font en continu.

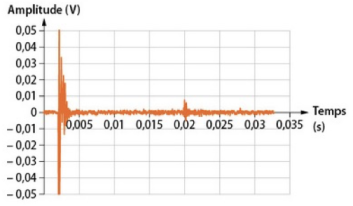
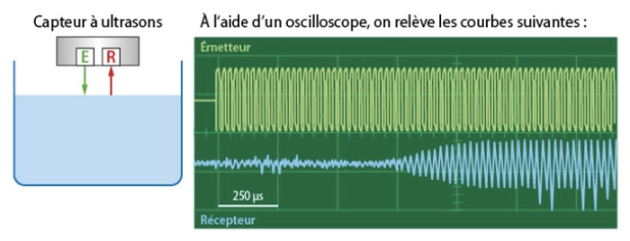
Complément : 📄 Document n°1 : Schéma de principe de l'installation industrielle et mesures effectuées à un instant donné

Complément : 📄 Document n°2 : Célérité du son dans l'eau et dans l'air à 20 °C

Célérité du son dans l'eau à \(20\ \mathrm{^\circ C}\) : \(\large{v_\textsf{son/eau}=1,5\cdot 10^3\ \mathrm{m\cdot s^{-1}}}\) ;
Célérité du son dans l'air à \(20\ \mathrm{^\circ C}\) : \(\large{v_\textsf{son/air}=340\ \mathrm{m\cdot s^{-1}}}\)

Question⚓

Q1. Déterminer la durée \(\Delta t\) entre l'émission et la réception d'une salve d'ultrasons après réflexion à la surface de l'eau.

← ANALYSER/RAISONNER

Lecture d'un enregistrement. Le signal reçu a une amplitude qui croît avant d'être constante.

Solution ⚓

Q1.

...

Question⚓

Q2. Calculer la distance \(d\) parcourue par les ultrasons entre leur émission et leur réception après réflexion à la surface de l'eau.

← S'APPROPRIER

Sélectionner l'information. Choisir la bonne célérité.

← RÉALISER

Effectuer un calcul en veillant à l'homogénéité des unités.

Solution ⚓

Q2.

...

Question⚓

Q3. En déduire la hauteur \(h\) d'eau dans la cuve à cet instant.

← S'APPROPRIER

Représenter la situation par un schéma. Reprendre le schéma et placer toutes les distances mentionnées dans cet exercice.

Solution ⚓

Q3.

...

💪 Exercice n°2 : Un sonar ⚓

L'enregistrement issu d'un sonar actif est donné ci-dessous.

Question⚓

Q4. Exploiter l'enregistrement pour déterminer la profondeur affichée sur l'écran.

Donnée : Célérité du son dans l'eau \({v_\textsf{son/eau}=1,5\cdot 10^3\ \mathrm{m\cdot s^{-1}}}\).

Solution ⚓

Q4.

...

💪 Exercice n°3 : L'atmosphère terrestre ⚓

Au sein de notre atmosphère terrestre, la célérité du son vaut \({340\ \mathrm{m\cdot s^{-1}}}\) au sol et \({280\ \mathrm{m\cdot s^{-1}}}\) à \(100\ \mathrm{km}\) d'altitude.

Question⚓

Q4. Identifier le(s) facteur(s) physique(s) responsable(s) de cette baisse de la célérité du son.

Solution ⚓

Q4.

La température est l'un des principaux facteurs. La célérité du son dépend de la température du milieu de propagation. À mesure que l'altitude augmente, la température de l'air diminue, ce qui réduit la vitesse de propagation du son.

La densité de l'air joue également un rôle crucial. À des altitudes plus élevées, l'air devient moins dense, ce qui affecte la manière dont les ondes sonores se propagent. Une densité plus faible entraîne une diminution de la célérité du son.

La composition de l'air peut aussi influencer la vitesse du son. À différentes altitudes, la composition de l'air peut varier, notamment en termes de pourcentage de vapeur d'eau et d'autres gaz, ce qui peut modifier la célérité du son.

💪 Exercice n°4 : Le palpeur ⚓

Les ultrasons sont utilisés dans de nombreux domaines et dans de multiples applications. Ils peuvent permettre entre autres de mettre en évidence des défauts dans une pièce, une paroi, mais également aussi de déterminer l’épaisseur d’une cloison. Ces différentes techniques sont basées sur les phénomènes de réflexion et de transmission (réfraction) d’une onde lorsqu’elle change de milieu de propagation.

Question⚓

Q5. En vous aidant d’internet, définir (avec vos mots à vous) les phénomènes de réflexion et de transmission d’une onde sonore lorsqu’elle change de milieu de propagation. Un schéma peut avantageusement compléter l’explication.

Solution ⚓

Q5.

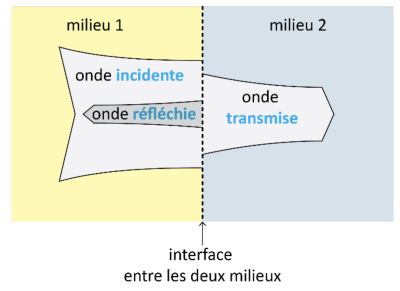
Lorsqu'une onde sonore passe d'un milieu à un autre, elle subit deux phénomènes principaux : la réflexion et la transmission.

Réflexion : Une partie de l'onde incidente ne pénètre pas dans le second milieu et est renvoyée dans le milieu d'origine. Ce phénomène se produit à l'interface entre les deux milieux. Par exemple, lorsqu'une onde sonore rencontre une surface dure, une partie de l'énergie sonore est réfléchie, ce qui signifie qu'elle rebondit sur la surface et retourne dans le milieu d'origine.

Transmission : Une autre partie de l'onde incidente continue de se propager dans le nouveau milieu. La transmission se produit également à l'interface entre les deux milieux. L'onde transmise peut subir des changements de vitesse et de direction en fonction des propriétés du nouveau milieu, comme sa densité et son élasticité.

Question⚓

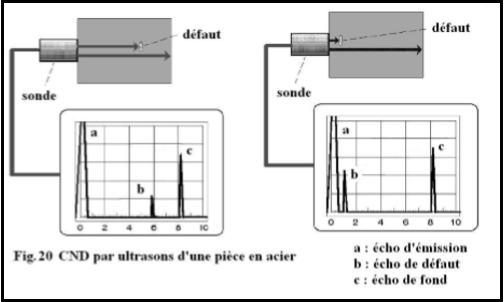
Q6. Commenter la situation ci-dessus. La sonde d’ultrasons s’appelle également un palpeur.

Solution ⚓

Q6.

Le palpeur va envoyer une onde ultrasonore dans la matière pour détecter les défauts qui se trouvent à l'intérieur (non visible). L'appareil mesure deux échos de défauts et on peut donc déduire l'intervalle de temps entre ces deux échos. À partir de cet intervalle de temps, on peut déduire la largeur de la faille en utilisant la vitesse de propagation des ultrasons dans le béton.

Question⚓

Q7. L’appareil mesure deux échos de défaut dans un mur de béton. L’intervalle de temps entre les deux défauts est de \(2,9\cdot 10^{-6} \ \mathrm{s}\). En déduire la largeur de la faille.

Donnée : \(\large{v_\textsf{son/béton}=3\ 000\ \mathrm{m\cdot s^{-1}}}\)

(Aide : À quoi correspond cet intervalle de temps. (Réponse : \(d = 8,7\ \ \mathrm{mm}\))

Solution ⚓

Q7.

On a un intervalle de temps \(\Delta t=2,9\cdot 10^{-5}\ \mathrm{s}\) entre l'écho b et le c.

On peut alors calculer la largueur de la faille :

\(\ell = v_\textsf{son/béton}\times \Delta t=3\ 000\times 2,9\cdot 10^{-6}\)

\(\ell = 8,7\cdot 10^{-3}\ \mathrm{m}=8,7\ \ \mathrm{mm}\)

💪 Exercice n°5 : Des calculs, toujours des calculs...⚓

Question⚓

Q8. Déterminer la période d’un son de fréquence :

a) \(15\ \mathrm{Hz}\) b) \(0,005\ \mathrm{Hz}\) c) \(360\ \mathrm{kHz}\)

Solution ⚓

Q8.

a) \(T=\dfrac{1}{f}=\dfrac{1}{15}=6,7\cdot 10^{-2}\ \mathrm{s}=67\ \mathrm{ms}\)

b) \(T=\dfrac{1}{f}=\dfrac{1}{0,005}=2,0\cdot 10^{2}\ \mathrm{s}\)

c) \(T=\dfrac{1}{f}=\dfrac{1}{360\cdot 10^{3}}=2,8\cdot 10^{-6}\ \mathrm{s}=2,8\ \mathrm{\mu s}\)

Question⚓

Q9. Déterminer la période d’un son de période :

a) \(5\ \mathrm{s}\) b) \(33\ \mathrm{ms}\) c) \(50\cdot 10^6\ \mathrm{s}\)

Solution ⚓

Q9.

a) \(f =\dfrac{1}{T}= \dfrac{1}{5} = 0,2 \ \mathrm{Hz}\)

b) \(f =\dfrac{1}{T}= \dfrac{1}{33\cdot 10^{-3}} = 30\ \mathrm{Hz}\)

c) \(f =\dfrac{1}{T}= \dfrac{1}{50\cdot 10^6} = 2 \times 10^{-8}\ \mathrm{Hz}\)

Question⚓

Q10. Déterminer la longueur d’onde dans l’air des sons de fréquence :

a) \(10\ \mathrm{Hz}\) b) \(40\ \mathrm{kHz}\) c) \(1,0\cdot 10^{3}\ \mathrm{Hz}\)

Solution ⚓

Q10.

a) \(\lambda=\dfrac{c}{f}=\dfrac{340}{10}=34\ \mathrm{m}\)

b) \(\lambda=\dfrac{c}{f}=\dfrac{340}{40\cdot 10^{-3}}=8,5\cdot 10^{3}\ \mathrm{m}\)

c) \(\lambda=\dfrac{c}{f}=\dfrac{340}{1,0\cdot 10^{3}}=0,34\ \mathrm{m}\)

Question⚓

Q11. Déterminer la fréquence des sons de longueur d’onde :

a) \(2,0\ \mathrm{m}\) b) \(4,0\ \mathrm{mm}\) c) \(8,0\cdot 10^{-3}\ \mathrm{m}\)

Solution ⚓

Q11.

a) \(f=\dfrac{c}{\lambda}=\dfrac{340}{2,0}=1,7\cdot 10^{2}\ \mathrm{Hz}\)

b) \(f=\dfrac{c}{\lambda}=\dfrac{340}{4,0\cdot 10^{-3}}=8,5\cdot 10^{4}\ \mathrm{Hz}\)

c) \(f=\dfrac{c}{\lambda}=\dfrac{340}{8,0\cdot 10^{-3}}=4,3\cdot 10^{-4}\ \mathrm{Hz}\)

💪 Exercice n°6 : Le diapason ⚓

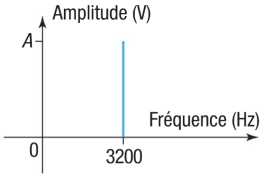
Un son pur est un son qui n'a pas d'harmonique.

Un diapason émet un son pur de fréquence \(880\ \mathrm{Hz}\).

Question⚓

Q12. Quelle est la longueur d'onde \(\lambda_\textsf{air}\) de ce son dans l'air ?

Solution ⚓

Q12.

\(\lambda_\textsf{air}=\dfrac{c}{f}=\dfrac{340}{800}=4,25\cdot 10^{-1}\ \mathrm{m}=42,5\ \mathrm{cm}\)

Question⚓

Q13. Au bout de quelle durée ce son est-il perçu par une personne située à \(10\ \mathrm{m}\) du diapason ?

Solution ⚓

Q13.

\(c_\textsf{son/air}=\dfrac{d}{\Delta t} \Longleftrightarrow \Delta t=\dfrac{d}{c_\textsf{son/air}}=\dfrac{10}{340}=2,9\cdot 10^{-2}\ \mathrm{s}\)

💪 Exercice n°7 : Le chant ⚓

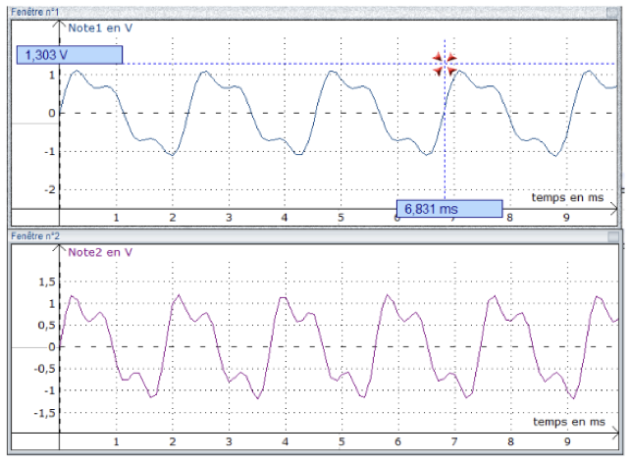
Un élève chante devant un micro, lui-même relié à une carte d'acquisition. Un ordinateur affiche la représentation graphique du signal délivré par le micro en fonction du temps. Voici les graphiques obtenus avec deux notes différentes :

Question⚓

Q14. Quelle note possède la fréquence la plus élevée ? Justifiez votre réponse en vous appuyant sur les graphiques, mais sans effectuer de calculs.

Solution ⚓

Q14.

La note dont la fréquence est la plus élevée est celle dont la durée du motif élémentaire est la plus petite (il se répètera davantage de fois en une même durée).

On voit graphiquement que la note n°2 possède une période plus faible \(\left( \approx 1,8\ \mathrm{ms}\right)\) que la note n°1 \(\left( \approx 2,0\ \mathrm{ms}\right)\).

Question⚓

Q15. Calculer la fréquence de la note n°1.

Solution ⚓

Q15.

\(f_\textsf{note n°1}= \dfrac{1}{T}=\dfrac{1}{2\cdot 10^{-3}}=5,0\cdot 10^{2}\ \mathrm{Hz}\)

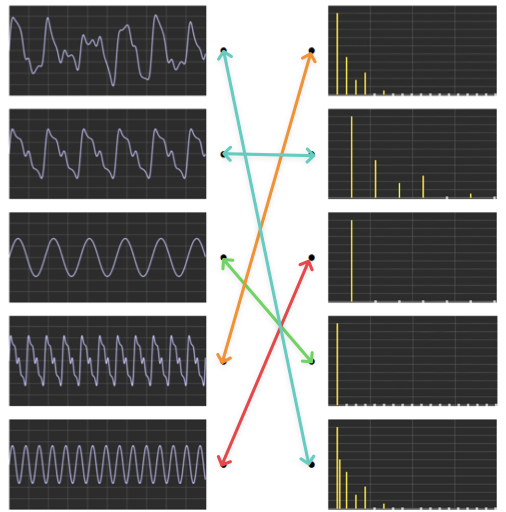
💪 Exercice n°8 : Deux instruments de musique ⚓

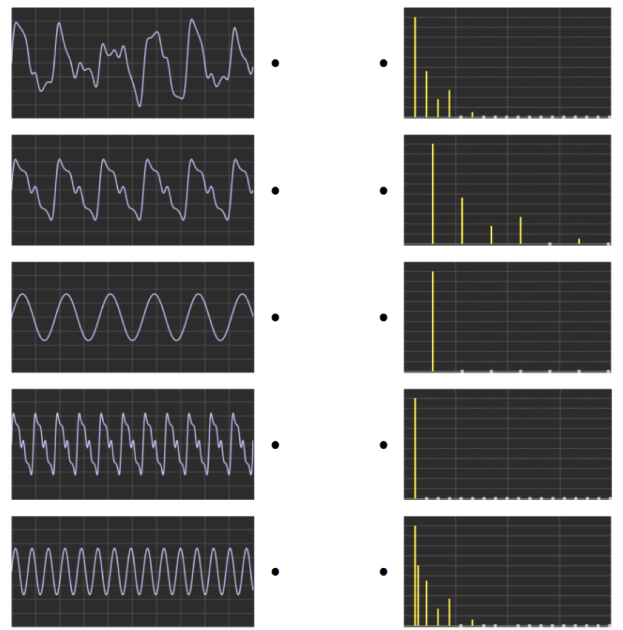
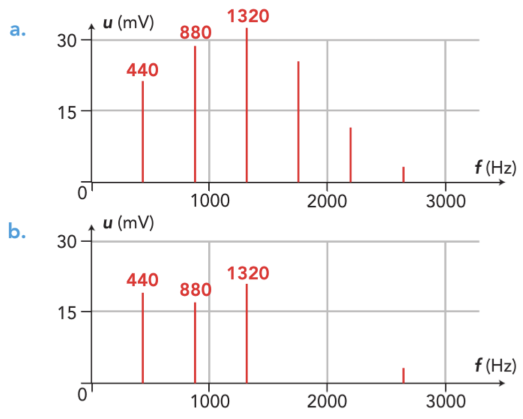
On a réalisé les spectres de deux notes de musique jouées par deux instruments.

Question⚓

Q16. Les notes ont-elles la même hauteur ? Justifier.

Solution ⚓

Q16.

Les deux notes ont la même hauteur car la hauteur d'un son est définie par la fréquence du fondamentale, ici \(440\ \mathrm{Hz}\).

Question⚓

Q17. Les timbres sont-ils identiques ? Justifier.

Solution ⚓

Q17.

En revanche, les timbres ne sont pas identiques car les deux notes ne possèdent pas les mêmes harmoniques (en nombre et en fréquence).

💪 Exercice n°9 : Le bouvreuil ⚓

Le bouvreuil est une espèce de passereau très discret dans nos campagnes. Il affectionne les haies et les lisères de forêt où il se cache. Les ornithologues peuvent le repérer grâce à son chant caractéristique.

L'analyse du chant du bouvreuil permet d'établir la décomposition de Fourier ci-contre :

Question⚓

Q18. Ce son est-il un son pur ou un son complexe ? Justifier.

Solution ⚓

Q18.

Il s'agit d'un son pur car dans la décomposition de Fourier il n'y a qu'une seule fréquence.

Question⚓

Q19. Quelle est la fréquence du son émis ?

Solution ⚓

Q19.

On a : \(f=3\200\ \mathrm{Hz}\)

Question⚓

Q20. Quelle sera l'allure du signal enregistré ?

Solution ⚓

Q20.

Comme il s'agit d'un son pur, le signal aura l'allure d'une sinusoïde.

💪 Exercice n°10 : Des signaux décomposés ⚓

Question⚓

Le tableau ci-dessous présente (à gauche) l'évolution temporelle de 5 signaux sonores et, à droite, 5 spectres.

Q21. Associer chaque spectre au bon signal sonore, sachant que tous les graphiques d'une même colonne de ce tableau sont représentés avec la même échelle.

Solution ⚓

Q21.