💪 Exercice n°1 : Le son dans les solides⚓
Cet exercice propose l'étude des deux types d'ondes sonores qui peuvent exister dans les solides.
Complément : 📄 Document n°1 : Les ondes sonores dans un solide
À l'échelle microscopique, un solide est constitué d'entités (atomes, molécules ou ions) empilés de manière ordonnée.
Le solide peut alors être le siège d'ondes sonores de deux types, appelées ondes de compression et ondes de cisaillement, représentés ci-dessous.

Question⚓
Q1. Définir une onde progressive.
Question⚓
Q2. Dans un solide, l'onde sonore est-elle mécanique ou électromagnétique ? Justifier en exploitant la définition du type d'onde choisi.
Solution⚓
Q2.
Dans un solide, l'onde sonore est une onde mécanique. Une onde sonore se propage par la vibration des particules du milieu à travers lequel elle se déplace. Dans le cas d'un solide, ces vibrations se transmettent de proche en proche entre les particules du matériau, ce qui permet à l'onde de se propager.
La définition d'une onde mécanique est une perturbation qui se propage dans un milieu matériel en transportant de l'énergie sans transporter de matière. L'onde sonore, étant une variation de pression (ou pression acoustique), correspond parfaitement à cette définition.
Question⚓
Q3. Parmi les ondes de compression et les ondes de cisaillement : lesquelles sont transversales ?lesquelles sont longitudinales ? Justifier en citant les définitions de ces deux types d'ondes.
Solution⚓
Q3.
Les ondes de compression et les ondes de cisaillement se distinguent par la direction de la perturbation par rapport à la direction de propagation de l'onde.
Les ondes de compression sont des ondes longitudinales. Dans ce type d'onde, la perturbation se produit dans la même direction que la propagation de l'onde. Un exemple typique est l'onde sonore dans l'air, où les variations de pression se propagent dans la direction de l'onde.
Les ondes de cisaillement, quant à elles, sont des ondes transversales. Dans ce type d'onde, la perturbation se produit perpendiculairement à la direction de propagation de l'onde. Un exemple courant est l'onde sismique de type S, où les particules du sol se déplacent perpendiculairement à la direction de propagation de l'onde.
Complément : 📄 Document n°2 : Les ondes sonores dans un solide
On réalise le protocole suivant :
Réaliser le montage représenté ci-dessous. Le capteur est sensible aux vibrations du métal et convertit cette vibration en signal électrique.

Régler la durée de l'acquisition à \(0,6\ \mathrm{ms}\).
Programmer un déclenchement sur l'entrée connectée au capteur.
Lancer l'enregistrement.
Frapper horizontalement l'extrémité gauche du barreau d'aluminium (afin de ne produire qu'une onde compression).
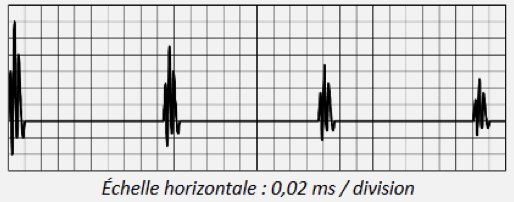
Résultat obtenu : signal reçu en fonction du temps
Question⚓
Q4. Le document n°2 présente une expérience permettant de mesurer la célérité des ondes de compression qui se propagent dans un bloc d'aluminium. Quel phénomène explique que le capteur reçoive un signal de même forme (bien qu'atténué) à intervalles de temps réguliers ?
Solution⚓
Q4.
Le phénomène qui explique que le capteur reçoive un signal de même forme (bien qu'atténué) à intervalles de temps réguliers est la réflexion des ondes de compression. Lorsqu'une onde de compression se propage dans un bloc d'aluminium, elle rencontre des interfaces ou des surfaces internes du matériau. À chaque interface, une partie de l'onde est réfléchie et retourne vers le capteur, tandis qu'une autre partie continue de se propager dans le matériau.
Cette réflexion répétée des ondes aux interfaces internes du bloc d'aluminium crée des échos qui sont captés à intervalles de temps réguliers. Chaque écho correspond à une onde réfléchie revenant au capteur après avoir parcouru une certaine distance dans le matériau. Bien que l'amplitude de ces échos diminue en raison de l'atténuation de l'énergie de l'onde, la forme du signal reste similaire car les caractéristiques de l'onde de compression ne changent pas.
Attention :
Pour les questions Q5 et Q6 : il sera tenu compte de la clarté de la rédaction, du vocabulaire scientifique employé et de la rigueur des calculs. Tout début de raisonnement, même inabouti, sera valorisé.
Question⚓
Q5. Exploiter les informations du Document n°2 pour montrer que la célérité des ondes de compression vaut : \(v_\textsf{Comp}=5,4\ \mathrm{km\cdot s^{-1}}\)
Solution⚓
Q5.
Le premier signal du résultat est l'arrivée de l'onde de compression issue du coup de marteau. Le signal suivant est la réflexion de ce premier signal après avoir fait un aller-retour dans le métal, et ainsi de suite.
On peut ainsi voir 3 ondes réfléchies pour une durée de \(\Delta t=18\ \textsf{divisions}=28\times 0,02 \ \mathrm{ms}=5,6\ \mathrm{ms}=5,6\cdot 10^{-3}\ \mathrm{s}\).
Ainsi l'onde de compression a parcouru une distance \(d=2\times 3 \times 50\ \mathrm{cm}=300 \ \mathrm{cm}=3,0\ \mathrm{m}\).
La célérité de l'onde de compression vaut donc : \(v_\textsf{Comp}=\dfrac{d}{\Delta t}=\dfrac{3,0}{5,6\cdot 10^{-5}}=5,4\cdot 10^{3}\ \mathrm{m \cdot s^{-1}}5,4\ \mathrm{km \cdot s^{-1}}\)
On admet que la célérité des ondes de cisaillement est inférieure à celle des ondes de compression.
Complément : Document n°3 : Mesure de la célérité des ondes de cisaillement
Le montage est le même que celui du document et l'acquisition est toujours déclenchée par le capteur, mais :
la durée de l'acquisition est réduite à \(100\ \mathrm{\mu s}\);
le barreau est frappé de manière oblique afin de faire naître les deux types d'ondes sonores simultanément.
Résultat :On obtient deux signaux de formes différentes, le second ayant un retard de \(60\ \mathrm{\mu s}\) sur le premier.
Question⚓
Q6. Le document n°3 présente une expérience permettant de mesurer la célérité des ondes de cisaillement. Exploiter ce document pour déterminer cette célérité \(v_\textsf{cis}\).
Solution⚓
Q6.
Le second signal a un retard de \(60\ \mathrm{\mu s}\) sur le premier, il arrive donc après le premier signal. En considérant que ce signal en retard n'est pas réfléchi, il aura parcouru une distance de \(d=50\ \mathrm{cm}=50\cdot 10^{-2}\ \mathrm{m}\) avec \(60\ \mathrm{\mu s}\) de plus que le signal de compression.
On a ainsi : \(\Delta t_2 - \Delta t_1=60\ \mathrm{\mu s}\)
On remplace alors ces durées par leurs expressions en fonction de la vitesse et de la distance parcourue :
\(\dfrac{d}{v_\textsf{cis}}-\dfrac{d}{v_\textsf{Comp}}=60\ \mathrm{\mu s}\)
\(\dfrac{d}{v_\textsf{cis}}-\dfrac{d}{v_\textsf{Comp}}=60\cdot 10^{-6}\ \mathrm{s}\)
\(d\times \left( \dfrac{1}{v_\textsf{cis}} -\dfrac{1}{v_\textsf{Comp}} \right) =60\cdot 10^{-6}\)
\(\dfrac{1}{v_\textsf{cis}} -\dfrac{1}{v_\textsf{Comp}}=\dfrac{60\cdot 10^{-6}}{d}\)
\(\dfrac{1}{v_\textsf{cis}} =\dfrac{60\cdot 10^{-6}}{d} + \dfrac{1}{v_\textsf{Comp}}\)
\(v_\textsf{cis} =\dfrac{1}{\dfrac{60\cdot 10^{-6}}{d} + \dfrac{1}{v_\textsf{Comp}}}\)
\(v_\textsf{cis} =\dfrac{1}{\ \ \ \dfrac{60\cdot 10^{-6}}{50\cdot 10^{-2}} + \dfrac{1}{5,4\cdot 10^{3}}\ \ \ }\)
\(v_\textsf{cis} = 3,3\cdot 10^{3}\ \mathrm{m \cdot s^{-1}}3,3\ \mathrm{km \cdot s^{-1}}\)
💪 Exercice n°2 : Fréquence, longueur d’onde et célérité des ultrasons⚓
Un élève dispose d'une source d'ultrasons de fréquence et longueur d'onde inconnues. Pour la mesurer il applique le
protocole du Document n°1. Le Document n°2 illustre les oscillogrammes obtenus lorsque les signaux sont en phase.
Complément : 📄 Document n°1 : Protocole de mesure d'une longueur d'onde
Le protocole suivant permet de mesurer la longueur d'onde des ondes sonores ou ultrasonores émises par une source.
Alimenter un émetteur d'ultrasons.
Placer deux récepteurs l'un derrière l'autre, dans l'alignement de la source à étudier.

Brancher chaque récepteur à une entrée d'un oscilloscope et observer l'évolution temporelle des signaux reçus.
Positionner les récepteurs afin que les deux signaux reçus soient en phase. Repérer la position du récepteur le plus éloigné de la source (récepteur 2).
Déplacer doucement le récepteur 2 afin de remettre les signaux en phase 20 fois.
Repérer la nouvelle position de ce récepteur et mesurer la distance \(D\) dont il a été déplacé.
Question⚓
Q8. La distance mesurée après application du protocole du Document n°1 vaut \(D = 17\ \mathrm{cm}\). En déduire la longueur d'onde des ultrasons émis par la source.
Solution⚓
Q8.
La longueur d'onde étant la distance que parcours l'onde en une période, dès lors que les signaux obtenus sont en phase après juste un seul décalage, alors la distance séparant les deux récepteurs est la longueur d'onde. Comme on a remis 20 fois les signaux en phase, on a donc 20 fois la longueur d'onde. On a donc \(\lambda=\dfrac{17\ \mathrm{cm}}{20}=0,85\ \mathrm{cm}=0,85\cdot 10^{-3}\ \mathrm{m}\).
Question⚓
Q9. La célérité des ondes sonores et ultrasonores, dans les conditions de l'expérience, vaut \(v=340\ \mathrm{m\cdot s^{-1}}\). En déduire la fréquence des ondes émises par la source étudiée. Vérifier qu'il s'agit bien d'ultrasons.
Solution⚓
Q9.
\(f=\dfrac{c}{\lambda}=\dfrac{340}{0,85\cdot 10^{-3}}=40\ 000\ \mathrm{Hz}\)
Comme \(f>20\ 000\ \mathrm{Hz}\), l'onde sonore est bien des ultrasons.
Question⚓
Q10. Exploiter l'oscillogramme du Document n°2 pour calculer la fréquence des ultrasons.