Complément :
Rappel : La thermodynamique est la science de tous les phénomènes qui dépendent de la température et de ses changements.
👨🎓 De la force pressante à la pression - Approche qualitative⚓
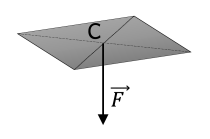
Définition : Force pressante
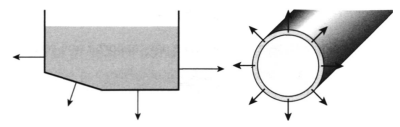
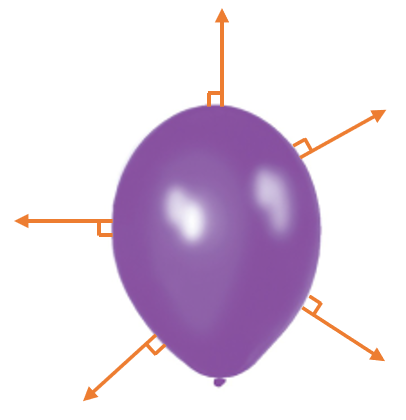
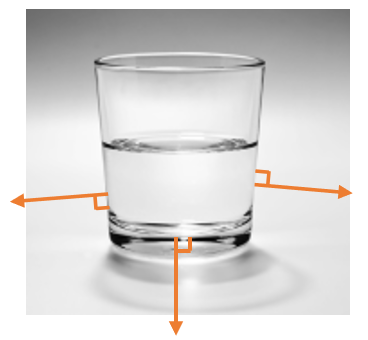
Un gaz ou un liquide contenu dans un récipient exerce une force sur les parois de celui-ci.
Cette force \(\vec{F}\), appelée force pressante, est toujours perpendiculaire aux parois.
Rappel : Représentation d'une force
La force est la grandeur physique associée à l'action mécanique.
Elle se caractérise par :
une direction (une ligne) ;
un sens (sens de parcours de la ligne) ;
une valeur (ou intensité) en newton (N) ;
un point d'application.
Une force localisée est modélisée par un vecteur-force \(\vec{F}\) avec pour point d'application le point de contact.
Une force répartie dans tout le volume (ou en surface) est modélisée par un vecteur-force appliqué au centre d'inertie \(G\) du corps.
Définition : Orientation des forces pressantes
Les forces pressantes sont toujours orientées du fluide vers la paroi, ce qui définit leur sens.
Elles sont perpendiculaires à la paroi, ce qui définit leur direction.
Le point d’application de la force pressante sur une paroi et la valeur de celle-ci dépendent de la façon dont la pression évolue sur cette paroi. Il existe deux cas de figure :
Pression uniforme (la même en tout point de la surface) sur l’ensemble de la paroi :
Exemples : Air ou le vent (un gaz) au niveau d’une cloison verticale, un liquide sur une paroi horizontale.
Dans ce cas : \(F = p_\text{rel} \times S\).
Avec \(p_\text{rel} \)la pression relative compte tenu de la hauteur de fluide au-dessus de la surface.
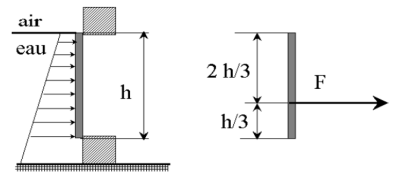
Pression variant linéairement avec la profondeur :
Exemples : Tout fluide incompressible (liquide) sur une paroi verticale.
Dans ce cas : \(F = p_\text{rel\ 1/2} \times S\).
Avec \(p_\text{rel\ 1/2}\) la pression relative à mi-profondeur.
Cette force s’exerce en un point situé à 2/3 de la hauteur de la paroi exposée au fluide incompressible, par rapport à la surface libre.
Représentation de la force pressante dans le cas où la pression est uniforme
Complément : Document n°1 : Lien entre force pressante et pression
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Vidéo sur support numérique.
Attention : Appel professeur
Faites vérifier vos réponses. Expliquer votre choix.
Définition : Unités de la pression
L'unité de la pression dans le système international est le pascal (Pa).
Il existe plusieurs unités de mesures pour la pression. Les trois unités couramment utilisées sont le millimètre de mercure (mmHg), le bar (bar) et le pascal (Pa).
\(1\ \mathrm{bar} = 10^5\ \mathrm{Pa}\)
\(1\ \mathrm{mmHg} = 133\ \mathrm{Pa}\)
La pression atmosphérique, notée \(p_\mathrm{atm}\), correspond à la pression de l'air qui nous entoure. Sa valeur est \(p_\mathrm{atm} \simeq 1,013\ \mathrm{bar} =1013\ \mathrm{hPa} = 101\ 300\ \mathrm{Pa}\).
Question⚓
Q3. (APP/RÉA) Effectuer les conversions suivantes :
Convertir en \(Pa\) :
a. \(2\, bar\)
b. \(3\, mbar\)
c. \(4\, Mbar\)
Convertir en \(bar\) :
d. \(2\,000\, 000\, Pa\)
e. \(2\cdot 10^5\, Pa\)
f. \(3\, kPa\)
Solution⚓
A-Q3.
Convertir en \(Pa\) :
a. \(2\, bar=2\times 10^5 \, Pa\)
b. \(3\, mbar=3\times 10^{-3} \times 10^5 \, Pa\)
\(=3\times 10^{2}\, Pa=300 Pa\)
c. \(4\, Mbar= 4\times 10^{6} \times 10^5 \, Pa\)
\(=4\times 10^{11}\, Pa=400 \ GPa\)
Convertir en \(bar\) :
d. \(2\,000\, 000\, Pa=\dfrac{2\,000\, 000}{10^5}\, bar=20\, bar\)
e. \(2\cdot 10^5\, Pa=\dfrac{2\cdot 10^5}{10^5}\, bar=2\, bar\)
f. \(3\, kPa=\dfrac{3\cdot 10^3}{10^5}\, bar=3\cdot 10^{-2}\, bar=30\, mbar\)
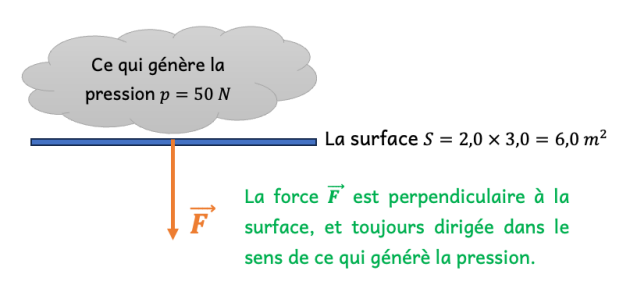
Définition : Force et pression
Q4. (APP) Indiquer ci-dessous la relation entre la force, la pression et la surface pressée avec les unités associées.
🏆 Quiz (§B.)⚓
→ Faire le quiz en cliquant sur le lien suivant : B. Quiz 🏆.
🏋️ S'entraîner⚓
1/ S'échauffer⚓
💪 Exercice n°1 : Pression d'un gaz dans un récipient⚓
Un gaz exerce une force pressante \(F =0,6\,\mathrm{N}\) sur une surface d'aire \(S = 10\,\mathrm{cm^2}\) du récipient qui le contient.
💪 Exercice n°2 : Pression et poids⚓
Rappel : Le poids d'un corps
Le poids \(\large{\vec{P}}\) d'un corps est la force exercée par la Terre sur cet objet. La valeur de cette force se calcule avec la formule suivante :
Avec :
\(\mathrm{P}\) : valeur du poids en \(\mathrm{N}\)
\(\mathrm{m}\) : masse du corps en \(\mathrm{kg}\)
\(\mathrm{g}\) : intensité de la pesanteur en \(\mathrm{N.kg^{-1}}\)
Complément : Données
\(g = 9,8 \,\mathrm{N.kg^{-1}}\)
La masse volumique moyenne de l'air est \(\rho_\mathrm{air} = 1,18\; \mathrm{kg.m^{-3}}\).
Question⚓
Q7. (RÉA) Calculer le poids d'une colonne d'air de \(10\,\mathrm{km}\) de hauteur et de \(1,0\,\mathrm{m^2}\) de surface au sol.
Solution⚓
C-Q7.
La colonne d'air correspond à un volume \(V=h\times S\). (Il est préférable de ne pas calculer la valeur du volume, ce n'est pas demandé... Mais si vous le calculez quand même : \(V=10\cdot 10^3\times 1=10\cdot 10^3 \, \mathrm{m^3}\) )
Pour calculer le poids, il faut la masse d'air, qui va s'obtenir avec la masse volumique avec la formule : \(\rho=\dfrac{m}{V} \Leftrightarrow m=\rho \times V\)
(Calcul inutile ici aussi... : \(m=\rho \times V=1,18\times 10\cdot 10^3=1,18 \cdot 10^4 \, \mathrm{kg}\) )
Le poids de la colonne d'air est donc :
\[\begin{array}{rll} \large {P } & = & {\large {m\times g } } \\ & = & {\large { \rho \times V \times g } } \\ & = & {\large { \rho \times h \times S \times g } } \\ & = & {\large { 1,18 \times 10\cdot 10^3\times 1 \times 9,81 } } \\ & = & {\large {{\color{blue} 1,2 \cdot 10^5 \;\mathrm{N} }} } \end{array}\]
💪 Exercice n°3 : Schématiser une situation⚓
Question⚓
Une surface rectangulaire de \(2,0 \ \mathrm{m}\) de largeur et de \(3,0 \ \mathrm{m}\) de longueur est soumise à une pression uniforme de \(50\ \mathrm{Pa}\).
Q9. (RÉA) Déterminer la valeur de la force pressante \(F\) agissant sur cette surface puis schématiser la situation en représentant cette force.
2/ Pour s'entraîner⚓
💪 Exercice n°4 : Bouteille en plastique⚓
Une bouteille en plastique ne contient initialement que de l'air. Elle est reliée à une pompe qui évacue cet air. La bouteille commence à s'effondrer sur elle-même dès que la pression à l'intérieur \(p_{int}\) vaut \(10,0\, \%\) de moins que la pression extérieure \(p_{ext}\), égale à \(1,013\cdot 10^5\,\mathrm{Pa}\).
Complément : Données :
\(g = 9,8 \,\mathrm{N\,kg^{-1}}\)
Question⚓
Q10. (RÉA) Calculer la pression \(p_\mathrm{int}\) à l'intérieur de la bouteille quand commence l'effondrement.
Solution⚓
C-Q10.
D'après l'énoncé, « la bouteille commence à s'effondrer sur elle-même dès que la pression à l'intérieur \(p_{int}\) vaut \(10,0\, \%\) de moins que la pression extérieure \(p_{ext}\), égale à \(1,013\cdot 10^5\,\mathrm{Pa}\). »
Donc, la pression interne vaut :
Question⚓
Q11. (ANA/RÉA) Dans ces conditions, quelle force pressante s'exerce sur l'aire \(s = 1,00\,\mathrm{cm^2}\) de la bouteille due à \(p_\mathrm{ext}\) ? et due à \(p_\mathrm{int}\) ?
Précisez pour chacune de ces forces comment elles s'exercent sur la paroi de la bouteille (direction et sens).
Solution⚓
C-Q11.
\(p_\mathrm{ext}\) engendre une force \(\vec{F}_\mathrm{ext}\) telle que :
\[\begin{array}{rll} \large { F_\mathrm{ext} } & = & {\large { p_\mathrm{ext} \times s } } \\ & = & {\large { 1,013\cdot 10^5\times 1,00\cdot 10^{-4} } } \\ & = & {\large {{\color{blue} 1,01\cdot 10^1\,\mathrm{N} }} } \\ & = & {\large {{\color{blue} 10,1\,\mathrm{N} }} } \end{array}\]Cette force \(\large{\vec{F}_\mathrm{ext}}\) s'exerce de l'extérieur vers l'intérieur de la bouteille perpendiculairement à la surface \(s\).
\(p_\mathrm{int}\) engendre une force \(\large{\vec{F}_\mathrm{int}}\) telle que :
\[\begin{array}{rll} \large { F_\mathrm{int} } & = & {\large { p_\mathrm{int} \times s } } \\ & = & {\large { 9,1\cdot 10^4\times 1,0\cdot 10^{-4} } } \\ & = & {\large {{\color{blue} 9,1\cdot 10^0\,\mathrm{N} }} } \\ & = & {\large {{\color{blue} 9,1\,\mathrm{N} }} } \end{array}\]Cette force \(\large{\vec{F}_\mathrm{int}}\) s'exerce de l'intérieur vers l'extérieur de la bouteille perpendiculairement à la surface \(s\).
Une force s'exerce toujours dans une direction et un sens donnés à partir d'un point d'application (voir le rappel « Représentation d'une force »
dans la partie A. de cette activité).
Question⚓
Q12. (ANA/RÉA) Quelle est la force pressante totale s'exerçant sur \(1,00\,\mathrm{cm^2}\) ? Bien justifier. (On pourra s'aider d'un schéma).
Préciser dans quelle direction et dans quel sens cette force pressante totale va s'appliquer.
Solution⚓
C-Q12.
Sur le même petit bout de surface d'aire \(s = 1,00\,\mathrm{cm^2}\) on a donc les deux forces qui s'exercent dans la même direction mais dans des sens opposés (voir réponse précédente).
Il faut donc soustraire les deux valeurs pour avoir la force pressante totale résultante :
Le choix de la soustraction se fait en considérant qu'une valeur de force ne peut pas être négative...
Cette force totale \(\large{\overrightarrow{F}_\mathrm{totale}}\) va s'exercer perpendiculairement à la surface \(s\) de l'extérieur vers l'intérieur de la bouteille.
Question⚓
Q13. (RÉA) Quelle masse \(m\) posée sur \(1,00\,\mathrm{cm^2}\) exercerait la même force ?
Solution⚓
C-Q13.
La force exercée par cette masse \(m\) correspond au poids de cette masse. On utilise donc la formule suivante : \(F_\mathrm{totale}=P=m\times g\). On a donc :
Question⚓
Q14. (APP/RÉA) L'aire totale de la bouteille est \(S_\mathrm{totale} = 855 \,\mathrm{cm^2}\). À quelle masse \(M\) correspond la force \(F_0\) résultant de la différence de pression exercée sur la totalité de la surface de la bouteille ?
Solution⚓
C-Q14.
La différence de pression exercée sur la totalité de la bouteille est : \(\Delta p = p_\mathrm{ext}-p_\mathrm{int}=1,013\cdot 10^{5}-9,1\cdot 10^{4}=\textbf{1,0}\cdot \textbf{10}^\textbf{4} \, \textbf{Pa}\).
On applique un raisonnement similaire qu'à la question Q11 et Q12 pour obtenir la masse équivalente \(M\) :
On a :
💪 Exercice n°5 : Dans la poudreuse⚓
La masse d'un randonneur, sac à dos compris est \(m = 80\,\mathrm{kg}\)
Rappel : Données
\(g = 9,8 \,\mathrm{N.kg^{-1}}\)
Question⚓
Q16. (RÉA) Représenter la force pressante du randonneur sur la neige.
Solution⚓
C-Q16.
Pour plus de simplicité, on modélisera cette force sur un seul des deux pieds du randonneur.
On doit choisir une échelle de représentation : \(2\,\mathrm{cm}\longleftrightarrow 7,8\cdot 10^{2} \,\mathrm{N} \).
Il faudra donc faire un vecteur (segment fléché) de 2 cm de longueur depuis un des pieds du randonneur.

Question⚓
Q17. (APP/RÉA) Calculer la pression exercée par le randonneur sur la neige :
en chaussures de marche dont chaque semelle a une surface de \(300\,\mathrm{cm^2}\) ;
équipé en raquettes, dont chacune a une surface de \(700\,\mathrm{cm^2}\). (On négligera la masse apportée par les raquettes).
Solution⚓
C-Q17.
Avec des chaussures :
\[\begin{array}{rll} \large { p_\mathrm{chauss.} } & = & {\large { \dfrac{ P_\mathrm{rando} }{ S_\mathrm{chauss.} } } } \\ & = & {\large { \dfrac{ 7,8\cdot 10^{2} }{ 2 \times 300 \cdot 10^{-4} } } } \\ & = & {\large { {\color{blue} 1,3 \cdot 10^{4} \,\mathrm{Pa} }} } \end{array}\]Avec des raquettes :
\[\begin{array}{rll} \large { p_\mathrm{raquettes} } & = & {\large { \dfrac{ P_\mathrm{rando} }{ S_\mathrm{raquettes} } } } \\ & = & {\large { \dfrac{ 7,8\cdot 10^{2} }{ 2 \times 700 \cdot 10^{-4} } } } \\ & = & {\large { {\color{blue} 5,6 \cdot 10^{3} \,\mathrm{Pa} }} } \end{array}\]
Question⚓
Q18. (ANA) Comparer ces deux pressions. Quel avantage cet équipement présente-t-il ?
Solution⚓
C-Q18.
On constate que \(p_\mathrm{raquettes} < p_\mathrm{chauss.}\). Les raquettes présentent donc l'avantage de permettre au randonneur d'exercer une pression plus faible sur la neige que s'il était en chaussures uniquement. De ce fait, avec les raquettes, le randonneur s'enfoncera moins dans la neige et pourra marcher plus facilement.
💪 Exercice n°6 : Pression admissible⚓
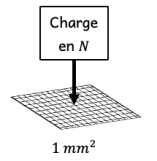
Pression admissible au sol
Pour pouvoir calculer les dimensions d'une fondation, li est nécessaire de con- naître la pression admissible au sol. La pression admissible \(\sigma\) est exprimée en \(\mathrm{N/mm^2}\).
S'il n'existe aucune étude préalable de la résistance du sol, on peut utiliser les valeurs ci-dessous pour les cas simples (par exemple les installations de chantier).
Si le sol est de qualité irrégulière (par exemple une zone de remblai), li est indispensable de procéder à une étude géotechnique.
Question⚓
Une fondation doit recevoir une charge de \(12 000\ \mathrm{N}\) environ par mètre linéaire, y compris le poids propre de la fondation. La résistance du terrain est estimée à \(0,2\ \mathrm{N/mm^2}\).
Q19. (ANA/REA) Calculer l’aire de la fondation à prévoir, puis sa largeur. Pour finir, à quelle masse correspondent ces \(12 000\ \mathrm{N}\).
Solution⚓
C-Q19.
La pression admissible ne doit pas dépasser \(0,2\ \mathrm{N/mm^2}\). Calculons alors la surface minimale \(S\) supportant cette pression admissible pour ce terrain avec une force \(F=12 000\ \mathrm{N}\) :
\(\sigma=\dfrac{F} {S} \Longleftrightarrow S=\dfrac{F} {\sigma} =\dfrac{12\ 000} {0,2}=60\ 000\ \mathrm{mm^2}=6,0\ \mathrm{m^2}\)
Pour \(1\ \mathrm{m}\) linéraire, il faut que la fondation fasse \(6\ \mathrm{m}\) de largeur.
Question⚓
Q20. (ANA/REA) Un pilier métallique constitué d’un socle carré en acier de \(40 \times 40 \ \mathrm{cm}\), soutien une charge de \(8\ 500 \ \mathrm{kg}\). La pression maximale admissible par le sol est de \(700\ 000 \ \mathrm{Pa}\). Commenter.
On donne : \(g=9,81\ \mathrm{N.kg^{-1}}\)
Solution⚓
C-Q20.
Le poids correspondant à la charge de \(8\ 500 \ \mathrm{kg}\) vaut : \(P=m\times g=8\ 500 \times 9,81=83,4 \cdot 10^3\ \mathrm{N}\)
La pression générée par le pilier est donc : \(p=\dfrac{F} {S} =\dfrac{83,4 \cdot 10^3} {40 \cdot 10^{-2}\times 40 \cdot 10^{-2}}= 5,21 \cdot 10^5\ \mathrm{Pa}= 521\ 000 \mathrm{Pa}\)
Cette force ne dépasse pas la charge maximale admissible du sol de : \(700\ 000 \ \mathrm{Pa}\).
Il faudrait cependant prendre en considération la masse du pilier lui-même, qu'on ne peut pas déterminer ici.
On peut chercher à déterminer cette masse :
La différence de pression entre la valeur maximale et celle calculée donne la valeur de la pression maximale que peut générer le pilier seul : \(p_\text{max}=700\ 000 - 5,21 \cdot 10^5=1,79 \cdot 10^5 \mathrm{Pa}\)
Ce qui correspond à une force : \(F_\text{max}=p_\text{max}\times S_\text{pillier}\). Or cette force est équivalent à une masse selon la relation : \(F=m\times g\). On a donc :
\(m=\dfrac{p_\text{max}\times S}{g}=\dfrac{1,79 \cdot 10^5\times \left(40 \cdot 10^{-2} \right)^2 }{9,81}=2,92\cdot 10^3\ \mathrm{kg}\)
Le pilier ne devra pas avoir une masse de plus 2,93 tonnes.
👨🎓 Interprétation simple⚓
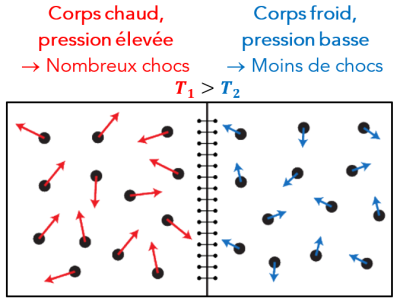
Complément : Document n°2 : Le mouvement désordonné d'un fluide
Les particules d'un système, quel que soit son état physique, sont en mouvement désordonné. Ce mouvement, appelé agitation thermique, est mesuré à l'échelle macroscopique par la température.
Dans l'exemple ci-contre, le volume constant et le nombre de particules identique. Le gaz du caisson de gauche a une température supérieure à celui de droite. La pression à gauche est donc plus élevée qu'à droite (loi des gaz parfaits).
Le nombre de chocs élastiques entre les particules et une paroi est d'autant plus important que la pression est grande.
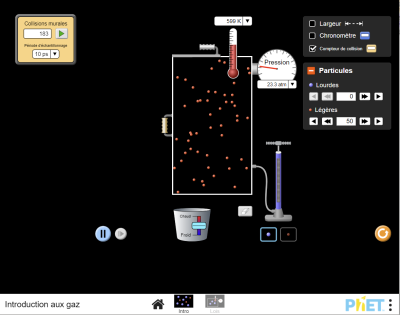
Il est possible d'utiliser la simulation suivante pour se rendre compte du mouvement des particules et des chocs.
→ Ouvrir la simulation, puis observer en utilisant ces réglages :
Onglet Intro ;
50 particules légères
Affichage des collisions murales
Température élevée (vers \(600\, K=326 \,\mathrm{^\circ C}\)
→ Faire descendre ensuite la température et observer.
Lien de la simulation : https://phet.colorado.edu/sims/html/gases-intro/latest/gases-intro_fr.html
Questions⚓
Question⚓
Q22. (VAL/COM) Comment expliquer que du gaz (ici l'air) exerce une pression sur la paroi de la bouteille ? (Aide : Que font les particules d'un système au niveau de la paroi d'un récipient ? Qu'est-ce que cela engendre ?)