💪 Exercice n°1 – Combustion du propane⚓
On étudie la combustion du propane \(\left(\ \ce{C3H8}\ \right)\)dans l’air.
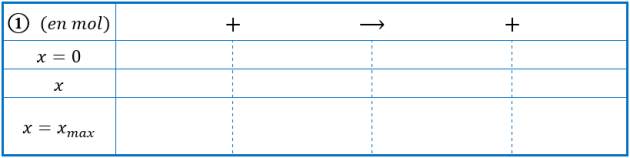
On réalise les 2 mélanges suivants :
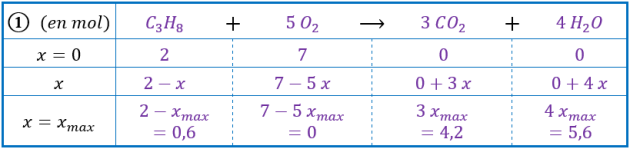
Mélange 1 : \(2,0\ \mathrm{mol}\) de propane et \(7,0\ \mathrm{mol}\) de dioxygène ;
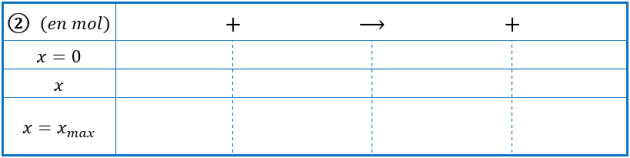
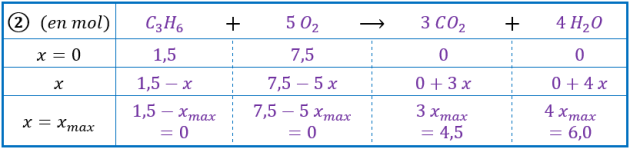
Mélange 2 : \(1,5\ \mathrm{mol}\) de propane et \(7,5\ \mathrm{mol}\) de dioxygène.
Question⚓
Q2. Pour le mélange 1, compléter le tableau d’avancement correspondant, puis déterminer l’avancement maximal et l’état final du système (c'est la dernière ligne du tableau d'avancement).
Solution partielle : \(x_\mathrm{max}=1,4\ \mathrm{mol}\)
Solution⚓
A3-Q2.
Détermination de \(\mathbf{x_\mathrm{max}}\) :
Si \(\ce{C3H8}\) est le réactif limitant : \(2-x_\mathrm{max}=0 \Leftrightarrow x_\mathrm{max}=2,0\ \mathrm{mol}\)
Si \(\ce{O2}\) est le réactif limitant : \(7-5\ x_\mathrm{max}=0 \Leftrightarrow x_\mathrm{max}=1,4\ \mathrm{mol}\)
L’avancement maximal est la plus petite des valeurs calculées précédemment, on a donc : \(\mathbf{x_\mathrm{max}=1,4\ \mathrm{mol}}\)
Le réactif limitant est donc le dioxygène.
Il reste plus qu'à remplir la dernière ligne du tableau d'avancement qui correspond à l'état final du système.
Question⚓
Q3. Même question pour le mélange 2.
Solution partielle : \(x_\mathrm{max}=1,5\ \mathrm{mol}\)
Solution⚓
A3-Q3.
Détermination de \(\mathbf{x_\mathrm{max}}\) :
Si \(\ce{C3H8}\) est le réactif limitant : \(1,5-x_\mathrm{max}=0 \Leftrightarrow x_\mathrm{max}=1,5\ \mathrm{mol}\)
Si \(\ce{O2}\) est le réactif limitant : \(7,5-5\ x_\mathrm{max}=0 \Leftrightarrow x_\mathrm{max}=1,5\ \mathrm{mol}\)
L’avancement maximal est la plus petite des valeurs calculées précédemment, on a donc : \(\mathbf{x_\mathrm{max}=1,5\ \mathrm{mol}}\)
Il n’y a pas de réactif limitant, car les réactifs ont été introduits dans les proportions stœchiométriques[*].
Il reste plus qu'à remplir la dernière ligne du tableau d'avancement qui correspond à l'état final du système.
💪 Exercice n°2 – Combustion de l’ammoniac⚓
On fait réagir \(2,55\ \mathrm{g}\) d’ammoniac \(\ce{NH_{3\ (g)}}\) avec \(10,0\ \mathrm{L}\) de dioxygène \(\ce{O_{2\ (g)}}\) pour obtenir du diazote \(\ce{N_{2\ (g)}}\) et de l’eau \(\ce{H2O_{(\ell)}}\).
Complément : Données
\(M_H=1,00\ \mathrm{g.mol^{-1}} \ \ \ \ M_N=14,0\ \mathrm{g.mol^{-1}} \ \ \ \ M_O=16,0\ \mathrm{g.mol^{-1}}\)
Volume molaire des gaz : \(V_M=24,0\ \mathrm{L.mol^{-1}}\)
Question⚓
Q5. Compléter le tableau d’avancement, déterminer l’avancement maximal et la composition de l’état final du système.
Solution partielle : \(x_\mathrm{max}=3,75\cdot{10}^{-2}\ \mathrm{mol}\)
Solution⚓
A3-Q5.
Il faut ici faire le bilan matière à l'état initial :
Ammoniac :
\(\left( n_{\ce{NH3}}\right)_i=\dfrac{\left(m_{\ce{NH3}}\right)_i}{M_{\ce{NH3}}}=\dfrac{2,55}{14,0+3\times1,00}=0,150\ \mathrm{mol}\)
Dioxygène :
\(\left(n_{\ce{O2}}\right)_i=\dfrac{\left(V_{\ce{O2}}\right)_i}{V_M}=\dfrac{10,0}{24,0}=0,417\ \mathrm{mol}\)
Détermination de \(\mathbf{x_\mathrm{max}}\) :
Si \(\ce{NH3}\) est le réactif limitant : \(0,150-4\ x_\mathrm{max}=0 \Leftrightarrow x_\mathrm{max}=3,75\cdot{10}^{-2}\ \mathrm{mol}\)
Si \(\ce{O2}\) est le réactif limitant : \(0,416-3\ x_\mathrm{max}=0 \Leftrightarrow x_\mathrm{max}=0,139\ \mathrm{mol}\)
L’avancement maximal est la plus petite des valeurs calculées précédemment, on a donc : \(\mathbf{x_\mathrm{max}=3,75\cdot{10}^{-2}5\ \mathrm{mol}}\)
Le réactif limitant est donc l’ammoniac.
Il reste plus qu'à remplir la dernière ligne du tableau d'avancement qui correspond à l'état final du système.
Question⚓
Q6. En déduire la masse d’eau et le volume de diazote obtenu.
Aide partielle : Utiliser la formule \(n_\mathrm{A}=\dfrac{V_A}{V_M}\) où \(V_M\) est le volume molaire des gaz.
💪 Exercice n°3 – Résolution graphique⚓
Pour obtenir du fer, on fait réagir dans un haut fourneau, de la magnétite \(\ce{Fe3O_{4\ (s)}}\) avec du monoxyde de carbone \(\ce{CO_{(g)}}\) pour obtenir du fer \(\ce{Fe_{(s)}}\) et du dioxyde de carbone \(\ce{CO_{2\ (g)}}\).
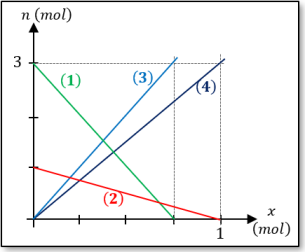
Le graphe ci-contre représente l’évolution en fonction de l’avancement des quantités de matières des réactifs et des produits de cette réaction chimique.
Question⚓
Q8. Identifier les 4 droites présentes dans le graphique.
Solution⚓
A3-Q8.
Les réactifs sont les espèces pour lesquels la quantité de matière diminue avec l’avancement de la transformation, donc courbe \(\definecolor{vert}{RGB}{0, 176, 80}\color{vert} \left(1\right)\) et \(\color{red}\left(2\right)\). Le \(\ce{CO}\) est celui qui disparait le plus vite, donc celui pour qui la courbe sera la plus pentue : la courbe \(\definecolor{vert}{RGB}{0, 176, 80}\color{vert} \left(1\right)\) est donc pour \(\ce{CO}\), et la courbe \(\color{red}\left(2\right)\) pour \(\ce{Fe3O4}\).
Autre justification : lorsque \(x=0,5\ mol\), il aura disparu \(4\ x=2\ mol\) de \(\ce{CO}\)et \(x=0,5\ mol\) de \(\ce{Fe3O4}\). Il faut donc que les courbes aient diminué d’autant, ce qui est bien le cas.
Les produits sont les espèces pour lesquels la quantité de matière augmente avec l’avancement de la transformation, donc courbe \(\definecolor{bleu}{RGB}{0, 112, 192}\color{bleu} \left(3\right)\) et \(\definecolor{bleufonce}{RGB}{0, 32, 96}\color{bleufonce} \left(4\right)\). Le \(\ce{CO2}\)est celui qui apparait le plus vite, donc celui pour qui la courbe sera la plus pentue : la courbe \(\definecolor{bleu}{RGB}{0, 112, 192}\color{bleu} \left(3\right)\) est donc pour \(\ce{CO2}\), et la courbe \(\definecolor{bleufonce}{RGB}{0, 32, 96}\color{bleufonce} \left(4\right)\) pour \(\ce{Fe}\).
Autre justification : lorsque \(x=0,5\ mol\), il se sera formé \(3x=1,5\ mol\) de \(\ce{Fe}\) et \(4\ x=2\ mol\) de \(\ce{CO2}\). Il faut donc que les courbes aient augmenté d’autant, ce qui est bien le cas.
Question⚓
Q9. À partir du graphique, déterminer l’avancement maximal ainsi que la composition de l’état final.
Aide : L'avancement maximal est atteint quand l'un des réactifs est totalement consommé. Qu'est-ce que cela signifie du point de vue de la courbe concernant ce réactif ?
Solution⚓
A3-Q9.
L’avancement devient maximal quand la quantité de matière d’un réactif devient nulle (réactif limitant) ou bien quand tous les réactifs sont entièrement consommés (mélange dans les proportions stœchiométriques).
Ici, on est dans le cas de la présence d’un réactif limitant car la courbe \(\definecolor{vert}{RGB}{0, 176, 80}\color{vert} \left(1\right)\) coupe l’axe des abscisses avant la courbe \(\color{red}\left(2\right)\).
Le réactif limitant est donc celui de la courbe \(\definecolor{vert}{RGB}{0, 176, 80}\color{vert} \left(1\right)\), donc \(\ce{CO}\).
On a donc \(x_{max}=0,75\ \mathrm{mol}\).
Donc à l’état final on a :
\(\left(n_{\ce{CO}}\right)_f=0\ \mathrm{mol}\) ;
\(\left(n_{\ce{Fe3O4}}\right)_f=0,25\ \mathrm{mol}\) ;
\(\left(n_{\ce{Fe}}\right)_f=2,25\ \mathrm{mol}\) ;
\(\left(n_{\ce{CO2}}\right)_f=3,0\ \mathrm{mol}\).