📄 Équation aux dimensions - [Document n°3]

L'équation aux dimensions est la formule qui permet de déterminer la dimension dans laquelle doit être exprimé le résultat d'une formule. C'est une équation de grandeurs, c'est-à-dire dans laquelle on représente les phénomènes mesurés par un symbole : par exemple, une longueur est représentée par la lettre « \(L\) ».

Grandeur de base

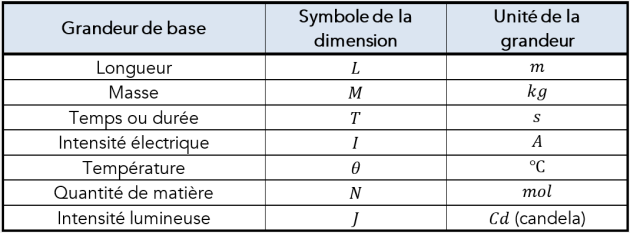
D'une manière générale il est possible d'exprimer la dimension de toutes les grandeurs physiques en fonction de sept dimensions de base. Les notations suivantes sont largement répandues :

Équation aux dimensions

L'équation aux dimensions est l'équation qui relie la dimension d'une grandeur dérivée à celles des sept grandeurs de base.

Dans une équation aux dimensions, la dimension de la grandeur dérivée \(X\) est couramment notée \(\left[X\right]\).

La forme générale d'une équation aux dimensions est : \(\left[X\right]=L^\alpha \ M^\beta \ T^\gamma \ I^\delta \ \theta \ ^\epsilon \ N^\zeta \ J^\eta\)

Où :

• \(L\), \(M\), \(T\), \(I\), \(\theta\), \(N\), \(J\) sont les dimensions respectives des sept grandeurs de base ;

• \(\ ^\alpha,\ \ ^\beta,\ \ ^\gamma,\ \ ^\delta,\ \ ^\varepsilon,\ \ ^\zeta,\ \ ^\eta\) sont les exposants respectifs des sept grandeurs de base.

  Ces derniers sont appelés exposants dimensionnels.