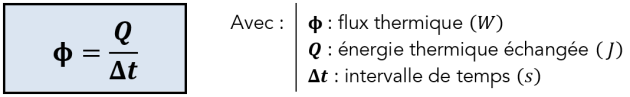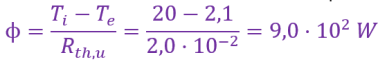🚩 Définitions [Rappels de 1ère année]⚓
Définition : Document n°1 - Transferts thermique et température
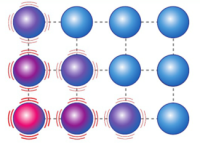
Un transfert thermique, appelé plus communément chaleur, est un transfert d'énergie microscopique désordonnée. L'exemple le plus courant d'un transfert thermique est le cas où deux corps en contact ont des températures différentes. Le corps le plus chaud va céder de l'énergie sous forme de chaleur au corps le plus froid : il y a transfert thermique entre les deux corps.
Complément : Document n°2 - Variation d'énergie interne lors d'un transfert thermique
La variation d'énergie interne \(\mathbf{\Delta U}\) d'un corps de masse \(\mathbf{m}\) dans un état condensé, n'échangeant de l'énergie que par transfert thermique \(\mathbf{Q}\) et passant de la température initiale \(\mathbf{T_i}\) à la température finale \(\mathbf{T_f}\) est :
Complément : Document n°3 - Capacité thermique
La capacité thermique \(\mathbf{C}\) d'un corps est l'énergie thermique que doit recevoir ce corps pour élever sa température d'un degré Celsius ou kelvin. Elle s'exprime en \(\mathbf{J.°C^{-1}}\) ou \(\mathbf{J.K^{-1}}\).
En pratique, on utilise la capacité thermique massique \(\mathbf{c}\), qui représente l'énergie thermique que doit recevoir 1 kg du corps pour élever sa température d'un degré Celsius ou kelvin.
On a alors :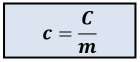 
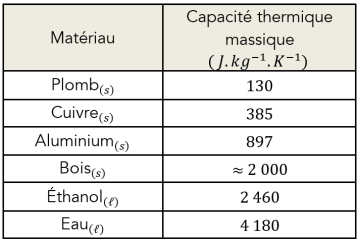
Exemple de capacités thermiques massiques :
💪 Exercice n°1⚓
Question⚓
Q4. Une cuillère à soupe sortant du congélateur est plongée dans un bol de soupe de 250 mL, initialement à 50 °C et finalement à 42 °C. Déterminer la variation d'énergie interne de la soupe constituée essentiellement d'eau.
Données : \(\mathrm{\rho_{eau}=1000\: g.L^{-1}}\) ; \(\mathrm{c_{eau}=4,18\cdot 10^{3}\: J.kg^{-1}.K^{-1}}\)
Solution⚓
A1.Q4. (Ex.1)
La température de l'eau baisse de 50 ℃ à 42 ℃. L'énergie perdue est donnée par :
\(\mathrm{\Delta U=Q=m_{eau}\cdot c_{eau}\cdot(T_f-T_i\ )=\rho_{eau}\cdot V\cdot c_{eau}\cdot(T_f-T_i\ )}\)
\(\mathrm{\Delta U=Q=1\ 000\cdot10^{-3}\times250\cdot10^{-3}\times4,18\cdot10^3\times(42-50)}\)
\(\mathrm{\Delta U=Q=-8,36\cdot 10^3 \: J}\)
👨🎓 Cas d'un système isolé⚓
Complément : Document n°4 - Énergie interne d'un système isolé
Si le système est thermodynamiquement isolé, c'est-à-dire qu'il n'y a aucun échange d'énergie et de matière avec le milieu extérieur alors son énergie interne \(U\) est constante et la variation d'énergie interne \(\Delta U\) est nulle :
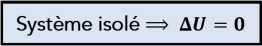
Complément : Document n°5 - Variation d'énergie interne et sous-système
Soit un système S pouvant être décomposé en deux sous-systèmes \(\mathrm{S_1}\) et \(\mathrm{S_2}\). La variation d'énergie interne \(\mathrm{\Delta U}\) du système \(\mathrm{ S}\) est égale à la somme des variations des énergies internes des deux sous-systèmes \(\mathrm{\Delta U_1}\) et \(\mathrm{\Delta U_2}\) :
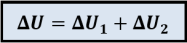
Rappel : Données pour les exercices suivants
\(\mathrm{\rho_{eau}=1000\: g.L^{-1}}\)
\(\mathrm{c_{eau}=4,18\cdot 10^{3}\: J.kg^{-1}.K^{-1}}\)
💪 Exercice n°2⚓
Question⚓
On mélange une quantité 1 d'eau de volume \(\mathrm{V_1=10\ L}\) à la température \(\mathrm{T_1=50\ °C}\) avec une quantité d'eau de volume \(\mathrm{V_2=30\ L}\) à la température \(\mathrm{T_2=10\ °C}\) dans un récipient considéré comme isolé.
Q5. Quelle est la température du mélange ?
💪 Exercice n°3⚓
Question⚓
Léa veut prendre un bain à 35 °C. Elle fait couler 100 L d'eau chaude à 65 °C, provenant de son cumulus électrique. Trouvant son bain trop chaud, elle y ajoute de l'eau froide à 20 °C. Si on considère la baignoire comme isolée.
Q6. Quel volume d'eau froide doit-elle faire couler ?
👨🎓 LES MODES DE TRANSFERTS THERMIQUES⚓
Complément : Document n°6 - Les 3 modes de transferts thermiques
La conduction :
Elle a lieu essentiellement dans les solides mais peut aussi se rencontrer, à une échelle beaucoup plus faible, dans les fluides. C'est un transfert thermique par contact sans transport de matière. D'un point de vue microscopique, les constituants du matériau communiquent à leurs voisins leur agitation thermique, tout en restant globale¬ment à la même place.
La convection :
Elle a lieu dans un fluide dont la température n'est pas homogène : la zone chaude, moins dense que la zone froide s'élève.
La convection est donc un transfert thermique porté par un mouvement de matière.
Le rayonnement :
Tout corps, en raison de sa température, émet des rayonnements thermiques. Le rayonnement est un transfert thermique qui ne nécessite pas de milieu matériel, les ondes électromagnétiques se déplaçant dans le vide.
💪 Exercice n°4⚓
Question⚓
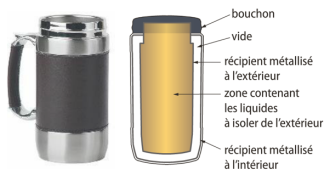
Q8. Voici ci-contre le schéma d'une bouteille thermos. Comment peut-elle, grâce à sa structure, limiter les 3 types de transferts thermiques ?
Solution⚓
A1.Q8. (Ex.4)
Les deux récipients ne sont pas en contact, limitant ainsi le transfert par conduction. Le vide a été fait entre les deux récipients, empêchant ainsi le transfert par convection. Les parois intérieures des deux récipients sont recouvertes de métal afin d'éviter le transfert par rayonnement.
💪 Exercice n°5⚓
🚩 Conclusion⚓
👨🎓 Le flux thermique⚓
Complément : Document n°7 - Le flux thermique
Les transferts thermiques, en fonction des milieux, peuvent se faire plus ou moins rapidement. Pour évaluer cette vitesse de transfert d'énergie, on crée une nouvelle grandeur appelée flux thermique, notée \(\mathbf{\phi}\) et s'exprimant en watt \(\mathbf{W}\). Le flux thermique correspond à l'énergie thermique \(\mathbf{Q}\) transférée par unité de temps \(\mathbf{\Delta t}\) :
Complément : Document n°8 - La résistance thermique
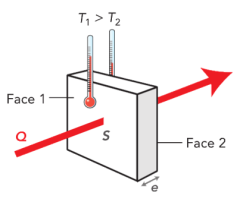
Une paroi plane, dont les deux faces sont à des températures différentes, est le siège d'un transfert thermique par conduction. Ce transfert se fait spontanément de la source chaude vers la source froide et est naturellement irréversible.
On définit la résistance thermique unitaire comme la capacité de la paroi à s'opposer au transfert thermique. Elle dépend de la conductivité thermique, de l'épaisseur et de la surface de la paroi traversée. La résistance thermique unitaire, notée \(\mathbf{R_{th,u}}\), est égale à :
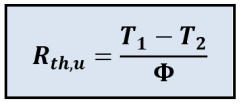
Il faut faire très attention à l'unité de la résistance thermique et du flux thermique !
On parle aussi de résistance thermique surfacique \(\mathbf{R_{th}}\) telle que : \(\mathrm{R_{th}=S\times R_{th,u}}\). L'unité de \(\mathbf{R_{th}}\) est \(\mathrm{m^2.K.W^{-1}}\). Pour utiliser cette grandeur, il faut donc connaître la surface de la paroi. Voir activité n°1 du prochain chapitre.
💪 Exercice n°6⚓
Une habitation présente une résistance thermique unitaire \(\mathrm{R_{th}=2,0\cdot{10}^{-2}\ K.W^{-1}}\). En hiver, la température extérieure est de \(\mathrm{T_e=2,1\ °C}\) et le thermostat est réglé pour maintenir une température intérieure de \(\mathrm{T_i=20\ °C}\) .
Données :
\(\mathrm{1\ W.h=3\ 600\ J}\)
Prix moyen du kW.h électrique en 2019 : 0,14 500 €
Cette habitation est entièrement chauffée par des radiateurs électriques, qui convertissent intégralement la puissance électrique en puissance thermique.
Question⚓
Q14. Quelle autre solution existe-t-il pour réduire le coût du chauffage de cette habitation ?