Activité n°1 : Intensité et niveau sonore - [Chapitre : Ondes sonores, Aspect énergétique]

Titre de l'activité : Activité n°1 : Intensité et niveau sonore - [Chapitre : Ondes sonores, Aspect énergétique]

Durée : 2h

Compétences

RÉA - Calculer, utiliser une formule
APP - Mobiliser les connaissances en rapport avec le problème
APP - Rechercher et extraire l'information
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
ANA - Exploiter ses connaissances, les informations extraites ou les résultats obtenus

Notions

Citer les deux grandeurs influençant la perception sensorielle : l’intensité et la fréquence d’un son.
Définir et mesurer le niveau sonore (dB).
Expliquer l’intérêt de la mesure du niveau sonore en dBA.
Situer, sur une échelle de niveaux sonores, des sons caractéristiques (vie courante et domaine professionnel) ainsi que les seuils d’audibilité et de douleur.

📑 Un peu de théorie (documents)⚓

📄 [Document n°1] - Pression acoustique ⚓

Complément : Variation de pression et son

Le son est la sensation auditive engendrée par la fluctuation périodique de la pression de l'air. Cette fluctuation se fait par rapport à la pression d'équilibre (la pression atmosphérique) et est ressentie au niveau de l'oreille.

Cette variation de pression est sinusoïdale.

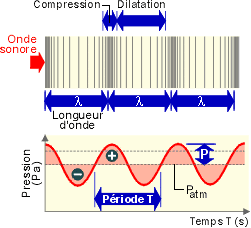
La variation de la pression se représente sous forme d'une onde sinusoïdale dont l'amplitude $P$ caractérise le niveau de pression acoustique.

Cette amplitude traduit l'intensité de la sensation,et est encore appelée le niveau sonore. Elle est mesurée en pascal (Pa). C'est la pression exercée par l'onde sonore sur le récepteur (tympan, membrane d'un microphone, ...).

Plus l'amplitude $P$ est grande, plus le son est fort.

📄 [Document n°2] - Intensité sonore ⚓

Complément : Transport d'énergie

Le son est une onde longitudinale qui transporte de l'énergie. Afin de caractériser ce transfert, on utilise la grandeur intensité sonore.

Définition : 📌 Intensité sonore

L'intensité sonore $I$ caractérise l'intensité du signal reçu par l'oreille, elle s'exprime en $\mathrm{W\,m^{-2}}$, c’est une énergie surfacique.

📄 [Document n°3] - Niveau sonore ⚓

Définition : 📌 Niveau sonore - 1ère partie

En acoustique, on indique couramment le niveau sonore en décibels (dB).

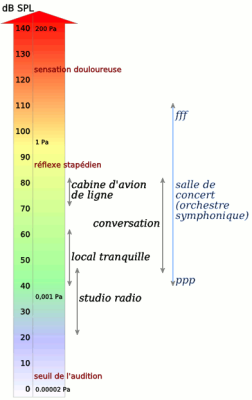
La plage de pressions donnant un niveau sonore perceptible s'étale sur un rapport de un à plusieurs millions. La perception du volume sonore est approximativement logarithmique : une augmentation donnée du volume correspond à multiplier la pression par un facteur identique. Pour cette raison, la mesure de bruit convertit très généralement la pression acoustique en décibels. On obtient ainsi une échelle qui va de 0 à 140 dB et rarement plus.

Définition : 📌 Niveau sonore - 2ème partie

Le niveau sonore exprime le rapport de puissance entre la puissance acoustique et une valeur de référence qui correspond à un son imperceptible,

$L = 10\ \log \left(\dfrac{P}{P_0}\right)$

$L = 10\ \log \left(\dfrac{p^2}{p_0^2}\right) = 20\ \log \left(\dfrac{p}{p_0}\right)$

$P$ la puissance acoustique en watt (W)

$P_0$ la puissance acoustique de référence en watt (W)

$p$ la pression acoustique en pascal (Pa)

$p_0 = 20\ \mathrm{\mu Pa}$ la pression acoustique de référence en pascal (Pa)

ou bien avec l’intensité sonore :

\[\begin{array}{lcl} {\fcolorbox{red}{white}{$ {\large \ \ \ \mathbf{ L = 10\ \log \left(\dfrac{I}{I_0}\right) } \ \ \ } $}} & \large \text{ avec :} & \begin{cases} {\large\ \mathbf{I}\ \text{ :} } & {\large \textsf{Intensité sonore en watt par mètre carré } \mathbf{W/m^2} } \\ {\large\ \mathbf{I_0}\ \text{ :} } & {\large \textsf{Intensité sonore de référence, } \mathbf{I_0=10^{-12}\ W/m^2} } \\ {\large\ \mathbf{L}\ \text{ :} } & {\large \textsf{Niveau d'intensité sonore en décibels } \mathbf{dB} } \end{cases} \end{array} \]

L’oreille humaine peut percevoir des sons d’intensités sonores comprises entre ${1,0\cdot10}^{-12}\ \mathrm{W/m^2}$ et

$25\ \mathrm{W/m^2}$.

Lorsque plusieurs sources sonores sont présentes, les intensités sonores de chaque source s’ajoutent.

Exemple :

Une pression acoustique efficace de $1 \ \mathrm{Pa}$ aura un niveau sonore de,

$L = 20\ \log \left(\dfrac{1}{20\times 10^{-6}}\right) = 94\ \mathrm{dB}$

Attention :

Lorsque plusieurs sources émettent, il faut additionner les intensités sonores des différentes sources au point de mesure et non les niveaux sonores.

Méthode : Calculer du niveau sonore de plusieurs sources

Pour calculer le niveau sonore de plusieurs sources il faut passer par ces étapes,

Déterminer les intensités sonores de chacune des sources.
Additionner ces intensités sonores $I_{tot} = \sum_n I_n$.
Calculer le niveau sonore $L_{tot}$ à partir de $I_{tot} $.

📄 [Document n°4] - Pondération du niveau sonore ⚓

Complément : Pondération A

La pondération A est la pondération standard des fréquences audibles ; elle a été conçue pour se rapprocher de la réaction de l'oreille humaine au bruit. L'oreille humaine n'est pas très sensible aux basses et hautes fréquences, mais entre 500 Hz et 6 kHz l'oreille est alors beaucoup plus sensible.

Le filtre de pondération A couvre la gamme entière des fréquences de 20 Hz à 20 kHz, mais sa façon de percevoir le son se rapproche de la sensibilité de fréquence de l'oreille humaine. Ainsi, la valeur pondérée A d'une source sonore est une approximation de la façon dont l'oreille humaine perçoit le bruit.

Les mesures réalisées en pondération A sont désignées par dB(A) pour annoncer que les informations sont en décibels pondérés A.

Complément : Pondération C

La pondération C est la pondération standard des fréquences audibles généralement utilisée pour la mesure du niveau de crête.

Les mesures réalisées en pondération C sont désignées par dB(C) pour annoncer que les informations sont en décibels pondérés C.

Complément : Pondération par octave

Fréquences (Hz)	63	125	250	500	1k	2k	4k	8k	16k
Pondération A (dB)	-26,2	-16,1	-8,6	-3,2	0	+1,2	+1,0	-1,1	-6,6
Pondération C (dB)	-0,8	-0,2	0	0	0	-0,2	-0,8	-3,0	-8,5

🏋️‍♂️ Un peu de pratique ⚓

Niveau sonore ⚓

Question⚓

Q1. Calculer le niveau d'intensité sonore d'une source d'intensité sonore $1,0\cdot10^{-5}\,\mathrm{W\,m^{-2}}$.

Question⚓

Q2. Quel est l’appareil de mesure qui permet de mesurer le niveau de pression acoustique ou le niveau d’intensité sonore ?

Solution ⚓

A1-Q2.

On utilise un sonomètre pour mesurer le niveau d’intensité sonore.

Intensité sonore ⚓

Question⚓

Un sonomètre mesure un niveau d'intensité sonore de $40\ \mathrm{dB}$.

Q3. Déterminer la formule permettant de calculer l'intensité sonore correspondante, puis en calculer sa valeur en $\mathrm{W/m^2}$.

Question⚓

Q4. Justifier que le niveau d’intensité sonore est plus aisé à exploiter que l’intensité sonore.

Solution ⚓

A1-Q4.

Les valeurs que peux prendre l’intensité sonore peuvent être très faible $10^{-12}\ \mathrm{W.m^{-2}}$, avec des puissances de 10 négatives, ce qui n’est pas facilement compréhensible, alors que le niveau d’intensité sonore prend des valeurs entre 0 et un peu plus de la centaine, donc bien plus simple à comprendre.

Question⚓

Q5. En utilisant le Doc.3-2^ème Partie, calculer les niveaux d’intensité sonore minimum et maximum supportés par nos oreilles. Ces résultats sont-ils en accord avec le Doc.3-1^ère Partie?

Solution ⚓

A1-Q5.

$L_\mathrm{min}=10\cdot\log{\left(\dfrac{1,0\cdot{10}^{-12}}{1,0\cdot{10}^{-12}}\right)}$

$L_\mathrm{min}=0\ dB$

$L_\mathrm{max}=10\cdot\log{\left(\dfrac{25}{1,0\cdot{10}^{-12}}\right)}$

$L_\mathrm{max}=134\ dB$

Ces résultats sont en accord avec les valeurs fournies par le Doc.3.

Question⚓

Q6. Calculer l’intensité sonore du seuil de danger (risque avéré pour l’audition) qui se situe vers $90 \mathrm{dB}$.

Solution ⚓

A1-Q6.

$I=I_0\times{10}^{\tfrac{L}{10}}=1,0\cdot{10}^{-12}\times{10}^{\tfrac{90}{10}}\color{blue}=1,0\cdot{10}^{-3}\ \mathrm{W.m^{-2}}$

À plusieurs ⚓

Deux instruments de musique jouent respectivement à $70 \ \mathrm{dB}$ et à $80 \ \mathrm{dB}$.

Question⚓

Q7. Quand ils jouent ensemble, quel est le niveau sonore ?

Question⚓

Q8. Quel est le niveau d'intensité sonore si 3 instruments jouent simultanément à $80 \ \mathrm{dB}$ ?

Question⚓

Q9. Montrer que lorsque le nombre de source identique double, le niveau sonore augmente de $3\ \mathrm{dB}$.

Solution ⚓

A1-Q9.

$L=10\cdot\log{\left(\ \frac{I}{I_0}\ \right)}$

avec $I^\prime=2\times I$, on a :

$L^\prime=10\cdot\log{\left(\ \dfrac{2\times I}{I_0}\ \right)}$

$L^\prime=10\cdot\log{\left(2\right)}+10\cdot\log{\left(\ \dfrac{I}{I_0}\ \right)}$

$L^\prime=3+10\cdot\log{\left(\ \dfrac{I}{I_0}\ \right)}$

$L^\prime=3+L$

Donc lorsque l‘intensité sonore double (nombre de source identique qui double), on a bien une augmentation de $3\ \mathrm{dB}$ du niveau sonore.

Un violon produit un son de niveau d’intensité sonore : $L=70\ \mathrm{dB}$.

Question⚓

Q11. Quel est le niveau sonore d’un orchestre de 5 violons ?

Solution ⚓

A1-Q11.

$L_{tot}=10\ \log{ \left( 10^{\tfrac{70}{10}}\times7\right)}=77\ \mathrm{dB}$

Question⚓

Q12. Combien de violon doivent jouer ensemble pour atteindre le seuil de danger ?

Solution ⚓

A1-Q12.

On chercher le nombre x de violons pour avoir $L_{tot}=90\ \mathrm{dB}$

\mathrm{dB}

$L_{tot}=10\cdot\log{\left({10}^{\tfrac{L}{10}}\times x\right)}$

$\dfrac{L_{tot}}{10}=\log{\left({10}^{\tfrac{L}{10}}\times x\right)}$

$10^{\tfrac{L_{tot}}{10}}=10^{\tfrac{L}{10}} \times x$

$x=\dfrac{{10}^{\tfrac{L_{tot}}{10}}}{{10}^{\tfrac{L}{10}}}$

$x=10^{\tfrac{L_{tot}}{10}-\tfrac{L}{10}}$

$x={10}^{\tfrac{90}{10}\ -\ \tfrac{70}{10}}={10}^2=100\ \textsf{ violons}$