Activité n°2 : Protection contre le bruit - [Chapitre : Ondes sonores, Aspect énergétique]

Titre de l'activité : Activité n°2 : Protection contre le bruit - [Chapitre : Ondes sonores, Aspect énergétique]

Durée : 2h

Compétences

RÉA - Suivre une procédure, un mode opératoire
RÉA - Calculer, utiliser une formule
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
ANA - Proposer une stratégie pour répondre à la problématique
ANA - Formuler une hypothèse
COM - Présenter la démarche suivie ou les résultats obtenus à l'aide d'un langage adapté
VAL - Interpréter les résultats obtenus

Notions

Citer les deux grandeurs influençant la perception sensorielle : l’intensité et la fréquence d’un son.
Définir et mesurer le niveau sonore (dB).
Expliquer l’intérêt de la mesure du niveau sonore en dBA.
Situer, sur une échelle de niveaux sonores, des sons caractéristiques (vie courante et domaine professionnel) ainsi que les seuils d’audibilité et de douleur.

Problématique

Un technicien participe à la mise en place d’un ventilateur puissant. On s’interroge sur les nuisances sonores qu’il va engendrer et en particulier les risques pour les techniciens travaillant dans son voisinage.

Comme l’oblige la législation, le ventilateur est fourni avec sa caractéristique spectrale de bruit dont on reporte les valeurs ci-dessous :

\(f\ \left( \ Hz\ \right)\)

125

250

500

1 000

2 000

4 000

8 000

\(L\ \left( \ dB\ \right)\)

L’objet de cette étude est de définir les risques auditifs liés à la présence de ce ventilateur dans l’environnement de travail et les protections envisageables.

Des documents sont fournis en fin d’activité.

📑 S'approprier ⚓

Question⚓

Q1. À l’aide des documents fournis, définir l’unité \(\mathrm{dB}\), expliquer l’intérêt de la mesure en \(\mathrm{dB}(A)\). Situer sur une échelle de niveaux sonores des sons caractéristiques ainsi que les seuils d’audibilité et de douleur (en \(\mathrm{Pa}\) et en \(\mathrm{dB}\)).

Solution ⚓

A2-Q1.

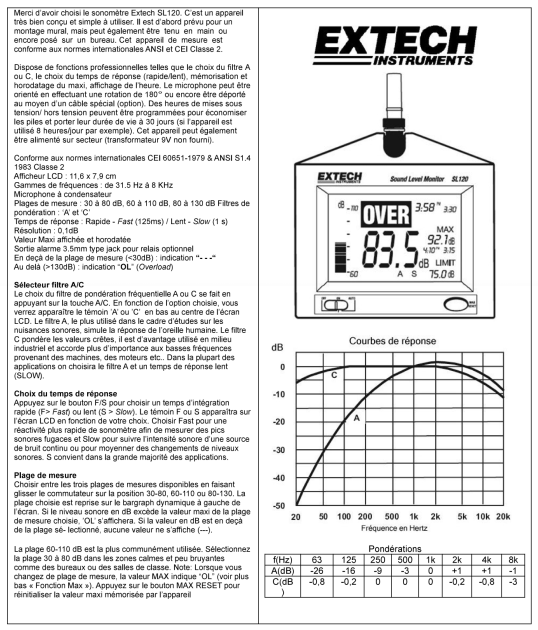
Il faut convertir les \(\mathrm{dB}\) en \(\mathrm{dB(A)}\) l’aide du Doc.1, puis calculer les intensités sonores de chaque fréquence. Ensuite on calculera l’intensité sonore totale puis le niveau d’intensité sonore.

\(I=I_0\times{10}^{\tfrac{L}{10}}\)

\(f\ \left( \ Hz\ \right)\)	63	125	250	500	1 000	2 000	4 000	8 000
\(L\ \left( \ dB\ \right)\)	95	92	95	91	88	80	76	66
\(L\ \left( \ dBA\ \right)\)	\(\color{blue}95-26\) \(\color{blue}=69\)	\(\color{blue}92-16\) \(\color{blue}=76\)	\(\color{blue}95-9\) \(\color{blue}=86\)	\(\color{blue}91-3\) \(\color{blue}=78\)	\(\color{blue}88-0\) \(\color{blue}=88\)	\(\color{blue}80+1\) \(\color{blue}=81\)	\(\color{blue}76+1\) \(\color{blue}=77\)	\(\color{blue}66-1\) \(\color{blue}=65\)
\(I\ \left( \ W.m^{-2}\ \right)\)	\(\color{blue}7,9\cdot{10}^{-6}\)	\(\color{blue}7,9\cdot{10}^{-5}\)	\(\color{blue}4,0\cdot{10}^{-4}\)	\(\color{blue}6,3\cdot{10}^{-5}\)	\(\color{blue}6,3\cdot{10}^{-4}\)	\(\color{blue}1,3\cdot{10}^{-4}\)	\(\color{blue}5,0\cdot{10}^{-5}\)	\(\color{blue}3,2\cdot{10}^{-6}\)

\[\begin{array}{lll} I_{tot}=7,9\cdot{10}^{-6}+7,9\cdot{10}^{-5}+4,0\cdot{10}^{-4}+6,3\cdot{10}^{-5}+6,3\cdot{10}^{-4}+1,3\cdot{10}^{-4}+5,0\cdot{10}^{-5}+3,2\cdot{10}^{-6} \\ \color{blue}I_{tot}=1,3\cdot{10}^{-2}\ \mathrm{W.m^{-2}} \\ \\ L_{tot}=10\log{\left(\ \dfrac{I_{tot}}{I_0}\ \right)}=10\log{\left(\ \dfrac{1,3\cdot{10}^{-2}}{1,0\cdot{10}^{-12}}\ \right)} \\ \color{red}L_{tot}=91\ \mathrm{dB(A)} \end{array}\]

Méthode plus rapide :

\[\definecolor{vert}{RGB}{0, 176, 80} \begin{array}{lll} \color{vert}\textsf{Méthode plus rapide :} \\ \color{vert} L_{tot}= 10\log { \left( {10}^{\tfrac{69}{10}}+{10}^{\tfrac{76}{10}}+{10}^{\tfrac{86}{10}}+{10}^{\tfrac{78}{10}}+{10}^{\tfrac{88}{10}}+{10}^{\tfrac{81}{10}} +{10}^{\tfrac{77}{10}}+{10}^{\tfrac{65}{10}} \right)}= 91\ \mathrm{dB(A)} \end{array} \]

Question⚓

Q2. Compte tenu de la législation en vigueur, indiquer comment l’utilisation du ventilateur nécessitera la mise en place d’actions spécifiques de prévention.

Solution ⚓

A2-Q2.

Comme le niveau d’intensité sonore est de \(\mathrm{91\ dB\left(A\right)\ >\ 80\ dB\left(A\right)}\), une action spécifique de prévention se déclenche : il faut mettre en place des protections individuelles comme un casque anti-bruit tel que le casque Peltor X1A ou X2A.

🔎 Analyser et 🖍 Réaliser ⚓

Par analogie avec le problème posé on vous propose d’étudier les nuisances sonores d’équipements techniques disponibles au lycée (CTA, PAC…). L’objectif est de mesurer le bruit émis par l’équipement et sa propagation dans le local.

Question⚓

Q3. Proposer un protocole expérimental permettant de mesurer l’atténuation du bruit, \(R\), en fonction de la distance. Vous préciserez, entre autres éléments, les réglages à effectuer pour le sonomètre (voir Document n°1).

Solution ⚓

A2-Q3.

L’atténuation du bruit se calcul en faisant \(R=L_\text{mesuré}-L_0\)

\(R=L_{final}-L_{initial}\) avec \(L_0\) mesuré à \(1\ \mathrm{m}\).

Question⚓

Q4. Effectuer les mesures et présenter les résultats à l’aide du tableur sous forme de tableau et d’un tracé (abscisse en échelle logarithmique).

Solution ⚓

A2-Q4.

✔ Valider et 📣 Communiquer ⚓

Question⚓

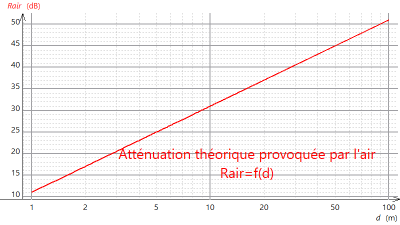
Q5. En espace libre, dans l’air, on peut estimer l’atténuation \(R_{air}\ \left(en\ dB\right)\) en fonction de la distance \(d\ \left(en\ m\right)\) par la formule : \(R_{air}=10\ \log{\ \left(4\pi d^2\right)}\). Tracer l’atténuation théorique provoquée par l’air et comparer aux mesures effectuées. Identifier les sources d’erreur.

Solution ⚓

A2-Q5.

Complément : Quelques informations supplémentaires

Lorsque la distance double, l’intensité acoustique est divisée par 4.

L’intensité acoustique est liée à la pression acoustique par la relation : \(I=\dfrac{p^2}{\rho\times c}\) donc :

\(p=\sqrt{I\times\rho\times c}\) et si \(I\) est divisé par 4, \(p\) est divisé par \(\sqrt4=2\).

Question⚓

Q6. Exploiter le graphique ci-contre en expliquant quantitativement comment évolue le niveau de bruit lorsqu’on double la distance par rapport à la source. Indiquer l’effet produit sur la pression acoustique exprimée en pascal et rattacher cet effet à l’impact sur les tympans du technicien subissant le bruit.

Solution ⚓

A2-Q6.

On voit sur le graphique que lorsqu’on double la distance l’atténuation est de \(6\ \mathrm{dB}\) (pour chaque doublement de distance). Donc le niveau de bruit diminue de \(6\ \mathrm{dB}\) lorsque la distance double.

p=\sqrt{I\times\rho\times c} et si I est divisé par 4, p est divisé par \sqrt4=2

Comme on a L_p=20\log{\left(\ \frac{p}{p_0}\ \right)}, alors une variation de L_p=6\ dB correspond à une pression acoustique :

\(p=p_0\times{10}^{\tfrac{L_p}{20}}=2\cdot{10}^{-5}\times{10}^{\tfrac{6}{20}}=4\cdot{10}^{-5}\ Pa\)

Donc sur le tympan, lorsqu’on double la distance, la pression va diminuer de \(4\cdot{10}^{-5}\ Pa\), ce qui est faible. Il va donc falloir s’éloigner davantage pour avoir une pression acoustique tolérable et sans danger.

Question⚓

Q7. Conclure sur les précautions envisageables pour se protéger du bruit en présence du ventilateur.

Solution ⚓

A2-Q7.

Pour le ventilateur, la pression acoustique vaut : \(p=p_0\times{10}^{\tfrac{91}{20}}=0,71\ \mathrm{Pa}\) ce qui est vraiment une valeur très importante. Même si on double la distance plusieurs fois, la pression acoustique restera trop importante et donc dangereuse. (et doubler la distance va rendre impossible le travail du technicien car s’il doit intervenir à un endroit précis, cet endroit ne pourra pas se déplacer…)

Il faut donc utiliser une protection individuelle comme un casque antibruit.

📃 Annexes (Documents)⚓

📄 [Document n°1] - Extrait de la notice d’un sonomètre ⚓

Complément :

Voir la version pdf pour un affichage plus grand.

📄 [Document n°2] - Code du travail – Protection des travailleurs exposés au bruit (Aide-mémoire juridique TJ16 – INRS)⚓

Complément :

Voir la version pdf pour un affichage plus grand.

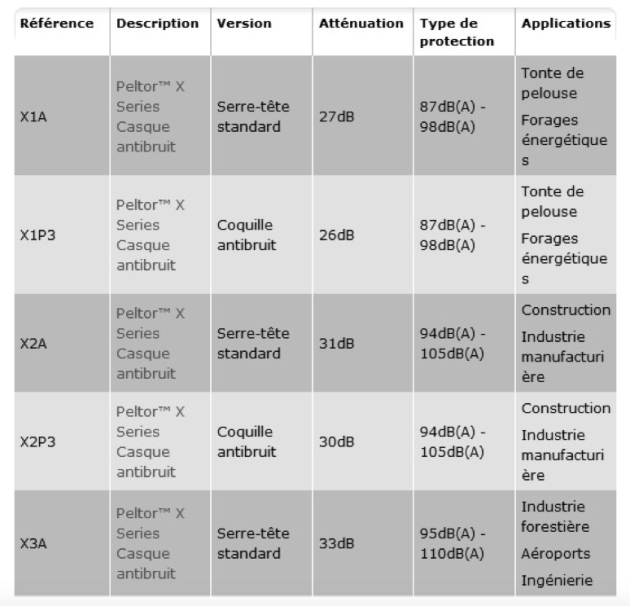
📄 [Document n°3] - Caractéristiques techniques de casques antibruit – 3M™ Peltor X séries ⚓

Complément :

Voir la version pdf pour un affichage plus grand.