Activité n°3 (Chap.1) : Équation de continuité (conservation du débit d'écoulement)

Définition :

En écoulement permanent (ou stationnaire) dans une canalisation en charge, la masse de fluide traversant l'ensemble des sections droites d'une canalisation par unité de temps reste la même. Le débit massique $Q_{\mathrm{m}}$ est constant.
La vitesse ne dépend pas du temps, elle est la même en chaque point pendant tout le temps de l'étude mais peut être différente en différents points de l'écoulement. Dans un écoulement permanent, la vitesse (comme la pression) est indépendante du temps mais dépend de la position.
Si le fluide est incompressible, sa masse volumique est constante (elle n'évolue pas dans le temps). Le débit volumique est alors constant lui aussi.

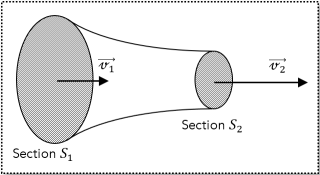
Cliquer sur le petit i pour avoir le lien direct vers l'animation → | Informations^[*]

À l'aide de l'animation utilisée lors de l'activité n°1, on peut établir la relation existant entre les vitesses moyennes $v_1$ et $v_2$ dans deux sections $S_1$ et $S_2$ de la canalisation. (voir la définition suivante)

Définition : Équation de continuité - (🚩À SAVOIR)

\[\fbox{$ {\Large {\color{blue} \text{ } S_1\times \mathrm{v}_1=S_2\times \mathrm{v}_2 \text{ } } } $}\]

→ L'objectif de ce début d'activité est de retrouver cette relation en étudiant un écoulement dans une canalisation.

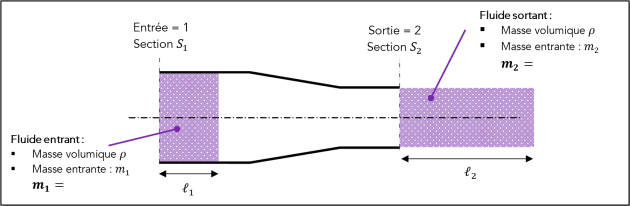
Complément : La situation - [Document n°1]

À un instant donné :

Il entre une masse $m_1$ de fluide de masse volumique $\large \rho$ par la section d'entrée 1 d'aire $S_1$.
Cette masse de fluide peut être représentée par une longueur $\large \ell_1$ (voir schéma ci-dessous).
Il sort une masse $m_2$ de fluide de masse volumique $\large \rho$ par la section de sortie 2 d'aire$ S_2$.
Cette masse de fluide peut être représentée par une longueur $\large \ell_2$ (voir schéma ci-dessous).

Le fluide se déplace à une vitesse ${v}_1$ dans la section $S_1$ et avec une vitesse ${v}_2$ dans la section $S_2$.

On peut écrire pour une durée $\Delta t$ : $\large \;\;\;\;\;\;{v}_1=\dfrac{\ell_1}{\Delta t} \;\;\;\;\;\;\; \text{et} \;\;\;\;\;\;\; {v}_2=\dfrac{\ell_2}{\Delta t}$

Question⚓

Q0. (RCO/RÉA) Compléter le schéma avec les relations sur les masse $m_1$ et $m_2$.

Solution ⚓

A3-Q0.

Question⚓

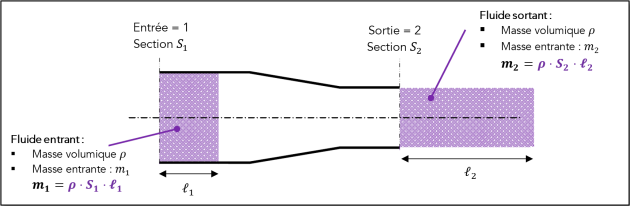
Q1. (RÉA) Écrire l'expression littérale de la masse $m_1$ et celle de la masse $m_2$ en fonction de la masse volumique, de la section traversée, de la vitesse et de la durée $\Delta t$.

Solution ⚓

A3-Q1.

\[ \begin{array}{lll} {\large m_1=\rho\cdot S_1\cdot\ell_1 } & & {\large m_2=\rho\cdot S_2\cdot\ell_2 } \\ {\large m_1=\rho\cdot S_1\cdot {v}_1\cdot \Delta t } & & {\large m_2=\rho\cdot S_2\cdot {v}_2\cdot \Delta t } \end{array}\]

Question⚓

Q2. (APP) Que peut-on dire de la masse du fluide entrant et de la masse du fluide sortant ? Pourquoi ?

Solution ⚓

A3-Q2.

Comme la matière ne disparaît pas dans la tuyauterie, la masse du fluide sortant est donc égale à la passe du fluide entrant.

Question⚓

Q3. (RÉA) Écrire alors la relation entre les sections et les vitesses d'écoulement.

Solution ⚓

A3-Q3.

\[ \begin{array}{rll} {\large m_1 } & {\large =} & {\large m_2 } \\ {\large \rho\cdot S_1\cdot {v}_1\cdot \Delta t } & {\large =} & {\large \rho\cdot S_2\cdot {v}_2\cdot \Delta t } \\ {\large \color{blue} S_1\cdot {v}_1 } & {\large \color{blue} =} & {\large \color{blue} S_2\cdot {v}_2 } \end{array}\]

Définition : Le débit volumique

À partir des équations précédentes, on peut démontrer que le débit volumique s'écrit :

\[\fbox{$ {\Large {\color{blue} \text{ } Q_\mathrm{V}=S\times {\mathrm{v}} \text{ } } } $}\]

Question⚓

Q4. (ANA/RÉA) À partir de l'expression du débit volumique vue dans l'activité n°2, $\large Q_\mathrm{V}=\dfrac{V}{\Delta t}$, démontrer la relation précédente.

Préciser le nom et l'unité des grandeurs suivantes : $S$, $S_1$, $S_2$, $v_\mathrm{moy}$, $v_1$, $v_2$ et $Q_\mathrm{V}$

Cette relation est à connaître.

Solution ⚓

A3-Q4.

$\large {Q_\mathrm{V}=\dfrac{V}{\Delta t}= \dfrac{S \times {\color{blue} \ell} } {{\color{blue} \Delta t}}=S\times {\color{blue} v}}$

Les sections $S$, $S_1$ et $S_2$ sont en $\mathrm{m^{2}}$, les vitesses moyennes ${v}_{moy}$ , ${v}_1$ et ${v}_2$ sont en $\mathrm{m.s^{-1}}$ et le débit $Q_\mathrm{V}$ volumique est en $\mathrm{m^{-3}.s^{-1}}$.

👨‍🎓 Dans le cas d'un écoulement permanent, la vitesse est-elle toujours le même dans les tuyaux ?⚓

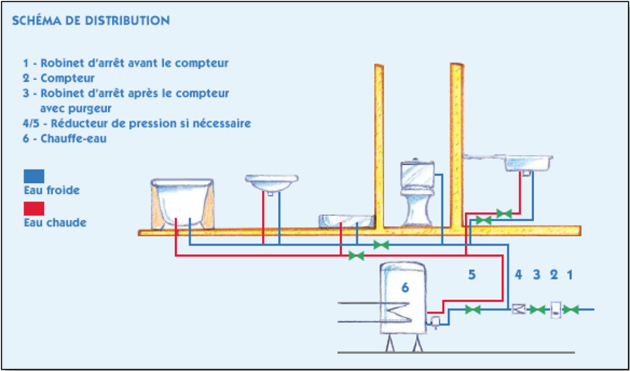
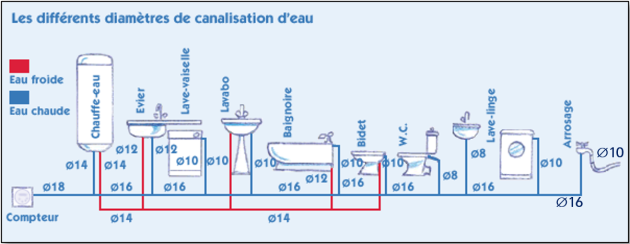
Dans la recherche de faire des économies sur sa consommation d'eau, M. Jean a ressorti le plan de distribution de l'eau dans son habitation. Un schéma vous est donné ci-dessous.

On y retrouve le compteur d'eau, le réducteur de pression et surtout il peut constater que l'eau circule dans des canalisations de diamètres différents.

M. Jean s'aperçoit ainsi que sur son installation, le diamètre de son tuyau d'arrosage est beaucoup plus petit (Ø 10) que celui qui arrive à son robinet (Ø16).

On notera :

$Q_\mathrm{m1}$ le débit massique dans la canalisation
$Q_\mathrm{m2}$ le débit massique dans le tuyau d'arrosage

Définition : Vitesse moyenne d'un fluide dans une section droite de canalisation - (🚩À SAVOIR)

La vitesse moyenne de déplacement d'un fluide dans une section droite de canalisation est définie par :

\[\fbox{$ {\Large {\color{blue} \text{ } \mathrm{v} =\dfrac{Q_\mathrm{V}}{S} \text{ } } } $}\]

Avec :

$Q_\mathrm{V}$ : Débit volumique du fluide en $\mathrm{m^{3}.s^{-1}}$
$S$ : Surface de la section de la canalisation en $\mathrm{m^{2}}$
$v$ : Vitesse moyenne de déplacement du fluide en $\mathrm{m.s^{-1}}$

Question⚓

Q5. (RCO/RÉA) En supposant que le débit massique ne change pas entre le tuyau d'arrosage et la canalisation, que peut-on dire du débit volumique ?

Solution ⚓

A3-Q5.

Comme le débit est supposé constant entre le tuyau et la canalisation, on peut écrire : $\large Q_\mathrm{m1}=Q_\mathrm{m2}$.

Or : $\large Q_\mathrm{m1}=\rho\times Q_\mathrm{V1}$ et $\large Q_\mathrm{m2}=\rho\times Q_\mathrm{V2}$ (voir activité n°2 & 3) avec $\large \rho$ la masse volumique de l'eau.

On a donc : $\large \rho\times Q_\mathrm{V1}= \rho\times Q_\mathrm{V2}$

C'est-à-dire : $\large Q_\mathrm{V1}=Q_\mathrm{V2}$

Le débit volumique est donc constant lui aussi.

Question⚓

Q6. (RÉA) Écrire la relation qui relie les vitesses d'écoulement ${v}_1$ et ${v}_2$ ainsi que les sections $S_1$ et $S_2$ des deux tuyaux.

Solution ⚓

A3-Q6.

$Q_\mathrm{V1}=Q_\mathrm{V1} \;\; \Longleftrightarrow \;\; \color{red} S_1 \times v_1=S_2 \times v_2$

Question⚓

Q7. (RÉA) Faire un petit schéma explicatif dans le cadre ci-contre en indiquant les vecteur vitesse et les sections.

Solution ⚓

A3-Q7.

Dans le cas de M. Jean, le diamètre de la canalisation est de $16\ \mathrm{mm}$ et celui du tuyau d'arrosage est de $10\ \mathrm{mm}$. Il faut $2\ \mathrm{min}$ à M. Jean pour remplir un arrosoir de $10\ \mathrm{L}$.

Question⚓

Q8. (RÉA) Calculer le débit massique d'eau $Q_\mathrm{m2}$ et le débit volumique $Q_\mathrm{V2}$ dans le tuyau d'arrosage de $10\ \mathrm{mm}$ de diamètre.

Solution ⚓

A3-Q8.

\[\begin{array}{rll} \large { Q_\mathrm{V2} } & \large{ =} & {\large { \dfrac{V_2}{\Delta t} } } \\ & \large{ =} & {\large { \dfrac{10\cdot 10^{-3} } { 2\times 60 } } } \\ & \large{ =} & {\large { \color{blue} 8,3 \cdot{10}^{-5}\ \mathrm{m^{3}.s^{-1}} }} \end{array}\]

Où $V_2$ est le volume d'eau écoulé pendant la durée $\Delta t$ (temps de remplissage de l'arrosoir), donc $V_2=10\ \mathrm{L}=10\cdot{10}^{-3}\ \mathrm{m^3}$

Il faut aussi convertir la durée en secondes, et le volume en $\mathrm{m^3}$.

\[\begin{array}{rll} \large { Q_\mathrm{m2} } & = & {\large { \rho \times Q_\mathrm{V2} } } \\ &\large{ =} & {\large { 1\ 000 \times 8,3 \cdot{10}^{-5} } } \\ & \large{ =} & {\large { \color{blue} 8,3 \cdot{10}^{-2}\ \mathrm{kg.s^{-1}} }} \end{array}\]

Avec $\large \rho=1\ 000\ \mathrm{kg.m^{-3}}$

Question⚓

Q9. (RÉA) En déduire la vitesse de l'écoulement ${v}_2$ dans le tuyau d'arrosage.

Solution ⚓

A3-Q9.

\[\begin{array}{ccl} \large { v_2 = \dfrac{ Q_\mathrm{V2}}{ S_2 } } & = & {\large { \dfrac{ Q_\mathrm{V2}}{ \pi \ \frac{d_{2}^{2}}{4} } }} \\ & \large{ =} & {\large { \dfrac{ 8,3\cdot 10^{-5} }{ \pi \ \frac{\left( 10\cdot 10^{-3} \right)^2 }{4} } }} \\ & \large{ =} & {\large { \color{blue} 1,1\ \mathrm{m.s^{-1}} }} \end{array}\]

Avec $S_2=\pi \dfrac{d_2^2}{4}$ où $d_2=10\ \mathrm{mm}=10\cdot{10}^{-3}\ \mathrm{m}$.

Question⚓

Q10. (RÉA) En déduire la vitesse de l'écoulement ${v}_1$ dans la canalisation.

Solution ⚓

A3-Q10.

On a montré à la question Q6 : $S_1\times {v}_1=S_2\times {v}_2$, donc :

\[\begin{array}{ccl} \large { v_1 = \dfrac{S_2 \times v_2 }{ S_1 } } & = & {\large { \dfrac{ Q_\mathrm{V2}}{ \pi \ \frac{d_{1}^{2}}{4} } }} \\ & \large{ =} & {\large { \dfrac{ 8,3\cdot 10^{-5} }{ \pi \ \frac{\left( 16\cdot 10^{-3} \right)^2 }{4} } }} \\ & \large{ =} & {\large { \color{blue} 0,41\ \mathrm{m.s^{-1}} }} \end{array}\]

Avec $S_1=\pi \dfrac{d_1^2}{4}$ où $d_1=16\ \mathrm{mm}=16\cdot{10}^{-3}\ \mathrm{m}$.

Question⚓

Q11. (APP) Conclure sur la vitesse.

Solution ⚓

A3-Q11.

Les vitesses d'écoulement sont différentes lorsque le diamètre de la canalisation change car il y a conservation du débit.

Définition :

Q12. (APP) Compléter l'encadré suivant.

Dans le cas d'un écoulement permanent, le débit étant le même dans toutes les portions d'un circuit, il y a conservation de la masse et on peut écrire :

\[\fbox{$ {\Large {\color{blue} \text{ } S_1\times \mathrm{v}_1=S_2\times \mathrm{v}_2 \text{ } } } $}\] Ou bien encore \[\fbox{$ {\Large {\color{blue} \text{ } S\times {\mathrm{v}}=Constante \text{ } } } $}\]

Avec :

$S_1$ et $S_2$ : Surface des sections du circuit en $\mathrm{m^{2}}$
$v_1$ et $v_2$ : Vitesse moyenne des écoulements en $\mathrm{m.s^{-1}}$

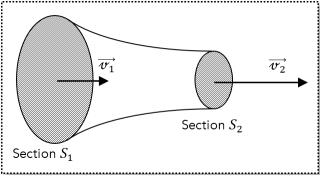
En écoulement permanent (stationnaire), la masse de fluide traversant l'ensemble des sections droites d'une canalisation par unité de temps reste la même. Le débit massique $Q_\mathrm{m}$ est constant.

Si les fluides sont considérés comme incompressibles, leur masse volumique est alors constante, leur débit volumique $Q_\mathrm{V}$ est donc constant aussi.

🏋️ Exemples d'application ⚓

💪 Exercice n°1 : Un fleuve tranquille ?⚓

Question⚓

Q13. (RÉA) Un fleuve a un débit de $850\ {m^3}/{s}$. Combien de litres d'eau s'écoulent en 1 heure ?

Aide : Faire attention aux unités ; Réponse : $\small V=3,06\ \mathrm{milliards\ de\ L}$

💪 Exercice n°2 : Canalisation de section variable ⚓

Une canalisation voit son diamètre passer de $D=400\ \mathrm{mm}$ à $d=200\ \mathrm{mm}$. On suppose que le débit d'écoulement est de 252 litres par seconde. Le fluide circulant est de l'eau $\left(\rho=1\ 000\ \mathrm{kg.m^{-3}}\right)$.

Question⚓

Q14. (RÉA) Faire un schéma de la situation en y faisant figurer les cotes.

Question⚓

Q15. (RÉA) Déterminer les vitesses moyennes d'écoulement pour chacune des deux sections de la canalisation.

Aide : Utiliser le débit volumique, puis utiliser l'équation de continuité ; Réponse : $\small v_1=2,01\ \mathrm{m.s^{-1}}\; ; \; v_2=8,02\ \mathrm{m.s^{-1}}$.

Question⚓

Q16. (RÉA) Calculer la valeur du diamètre de tuyauterie qu'il faudrait pour avoir une vitesse moyenne de $5,00\ \mathrm{m.s^{-1}}$.

Aide : Utiliser l'équation de continuité ; Réponse : $\small d_1=253\ \mathrm{mm}$.

Question⚓

Q17. (RÉA) Calculer la valeur du débit massique.

Aide : Utiliser la formule du débit massique ; Réponse : $\small Q_\mathrm{m}=252\ \mathrm{kg.s^{-1}}$.

💪 Exercice n°3 : Alimentation d'un réservoir ⚓

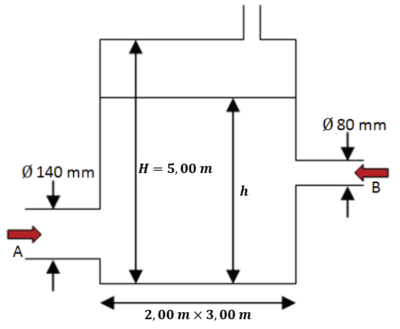
Deux canalisations A (de diamètre $140\ \mathrm{mm}$) et B (de diamètre $80,0\ \mathrm{mm}$) alimentent un réservoir parallélépipédique $\left(L\times P\times H=2,00\ \mathrm{m}\times3,00\ \mathrm{m}\times5,00\ \mathrm{m}\right)$.

La vitesse moyenne du fluide en A est de $0,620\ \mathrm{m.s^{-1}}$, celle en B vaut $0,500\ \mathrm{m.s^{-1}}$.

Question⚓

Q18. (RÉA) Déterminer la vitesse de montée $v_\text{montée}$ de l'eau dans le réservoir.

Aide : Bien lister les données fournies. Que vaut le volume du réservoir ? Qu'est-ce qui permet le remplissage du réservoir ? Quelle grandeur peut être associée à ce remplissage ? Écrire la formule littérale. Utiliser la formule donnée avant la Q5 pour déterminer la vitesse de montée ; Réponse : $\small v_\text{montée}=2,01\ \mathrm{mm.s^{-1}}$.

Question⚓

Q19. (RÉA) Déterminer le temps de remplissage depuis $h=0\ \mathrm{m}$.

Aide : Utiliser la formule du débit volumique ; Réponse : $\small \Delta t=41\ \mathrm{min}\ 20\ \mathrm{s}$.