Objectifs
Découvrir comment se propage un son et calculer la vitesse de propagation d'un son dans différents milieux.
👨🎓 Nature ondulatoire du son et propagation⚓
📄 Documents⚓
Complément : Document n°1.a : Qu'est-ce qu'une onde ?
Une onde est la propagation d'une perturbation produisant sur son passage une variation réversible des propriétés physiques locales du milieu. Elle se déplace avec une vitesse déterminée qui dépend des caractéristiques du milieu de propagation. Une onde transporte de l'énergie sans transporter de matière.
Source : http://fr.wikipedia.org/wiki/Onde
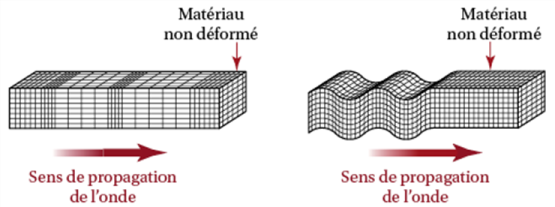
Une onde peut être transversale ou longitudinale.
Complément : Document n°1.b : Animation sur les ondes transversales et longitudinales
Regarder l'animation suivante pour mieux comprendre la différence entre ces deux types d'ondes :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Lien de cette animation avec QR-Code : https://dgxy.link/YRYyD 
Complément : Document n°2 : Ondes sonores
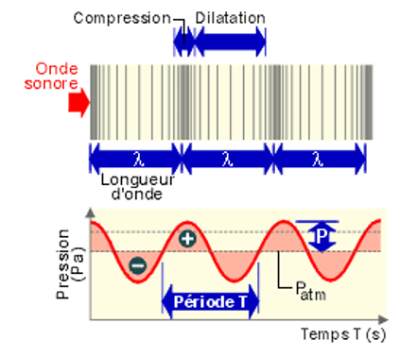
Le son est l'onde correspondant à la vibration d'un support qui se propage de proche en proche grâce aux propriétés élastiques du milieu. Si elle reste toujours basée sur le même principe, la propagation d'une onde sonore varie suivant que le milieu est compressible (air...) ou incompressible (eau, acier...).
Pour un milieu compressible (le plus souvent un fluide), l'onde sonore se déplace sous la forme d'une variation de pression. Sans se déplacer réellement, les molécules présentes dans le milieu peuvent osciller autour de leur position d'origine en avançant et reculant d'une ou deux tailles, mais en revenant toujours à la position d'origine.
Par exemple pour un haut-parleur, la membrane externe avance et recule en fonction du son à émettre, ce qui génère une surpression ou une dépression pour les molécules en contact avec elles. De proche en proche cette variation de pression se propage aux autres molécules en s'éloignant du haut-parleur. L'avancement de l'onde correspond à la succession des zones de compression et de raréfaction. Ces zones passent successivement d'un état à l'autre, permettant à l'onde d'avancer.
Dans un milieu non compressible, les molécules ont moins de liberté. Leurs déplacements relatifs sont d'autant plus limités que le milieu est dense et solide. Le déplacement de l'onde se fait également grâce au déplacement des atomes ou molécules, mais sur des distances beaucoup plus faibles.
Complément : Document n°3 : Vitesse de propagation d'un son dans l'air
Dans l'air, la vitesse d'une onde sonore dépend de la température de l'air θ et peut être calculée avec
la relation suivante :
\(c_\mathrm{air}\) en mètre par seconde (\(\mathrm{m\, s^{−1}}\) )
\(\theta\) en degré Celsius (°C ou K)
Cette relation est valable pour des températures comprises entre −20 °C et 40 °C et la valeur obtenue est précise à 0,2 %.
Complément : Document n°4 : Vitesse de propagation d'un son dans un liquide
La vitesse de propagation d’un son dans un liquide dépend de la masse volumique \(\rho\) du liquide et de son coefficient de compressibilité adiabatique \(\chi\) :
\(c_\mathrm{liquide}\) en mètre par seconde (\(\mathrm{m\, s^{−1}}\) )
\(\rho\) en kilogramme par mètre cube (\(\mathrm{kg\, m^{−3}}\) )
\(\chi\) en par pascal (\(\mathrm{Pa^{−1}}\) )
Complément : Document n°5 : Vitesse de propagation d'un son dans un solide
La vitesse de propagation d’un son dans un solide dépend de la masse volumique \(\rho\) du solide et de son module de Young \(E\) :
\(c_\mathrm{solide}\) en mètre par seconde (\(\mathrm{m\, s^{−1}}\) )
\(\rho\) en kilogramme par mètre cube (\(\mathrm{kg\, m^{−3}}\) )
\(E\) en pascal (\(\mathrm{Pa}\) )
Le module de Young correspond à la contrainte mécanique qu'il faut appliquer à un matériau pour qu'il double sa longueur. Plus \(E\) est grand plus le matériau est rigide.
Complément : Document n°6 : Données physiques de quelques liquides
Liquide | Masse volumique ( \(\mathrm{kg\, m^{−3}}\) ) | Coefficient de compressibilité adiabatique \(\chi\) ( \(\mathrm{Pa^{−1}}\) ) |
|---|---|---|
Alcool | 789 | \(9,4 \times 10^{−10}\) |
Eau | 1000 | \(4,9 \times 10^{−10}\) |
Eau de mer | 1000 à 1032 | \(4,0 \times 10^{−10}\) |
Complément : Document n°7 : Données physiques de quelques solides
Solide | Masse volumique ( \(\mathrm{kg\, m^{−3}}\) ) | Module de Young \(E\) ( \(\mathrm{GPa}\) ) |
|---|---|---|
Acier | 7500 à 8100 | 210 |
Béton | 2200 | 20 à 40 |
Brique | 1900 à 2000 | 14 |
Verre | 2530 | 69 |
Polystyrène | 1040 à 1060 | 2,8 à 3,4 |
❔ Questions⚓
Question⚓
Q5. Calculer la vitesse de propagation d'un son dans chaque liquide du document 6.
Solution⚓
A3-Q5.
Alcool :
\(c_\mathrm{liquide1}=\sqrt{\ \dfrac{1}{\rho\times\chi}\ }\)
\(c_\mathrm{liquide1}=\sqrt{\ \dfrac{1}{789\times9,4\cdot{10}^{-10}}\ }\)
\(\color{blue}c_\mathrm{liquide1}=1\ 161\ \mathrm{m.s^{-1}}\)
Eau :
\(c_\mathrm{liquide2}=\sqrt{\ \dfrac{1}{1\ 000\times4,9\cdot{10}^{-10}}\ }\)
\(\color{blue}c_\mathrm{liquide2}=1\ 429\ \mathrm{m.s^{-1}}\)
Eau de mer : (pour \(\rho=1\ 000\ \mathrm{kg.m^{-3}}\))
\(c_\mathrm{liquide3}=\sqrt{\ \dfrac{1}{1\ 000\times4,0\cdot{10}^{-10}}\ }\)
\(\color{blue}c_\mathrm{liquide3}=1\ 581\ \mathrm{m.s^{-1}}\)
Eau de mer : (pour \(\rho=1\ 032\ \mathrm{kg.m^{-3}}\))
\(c_\mathrm{liquide4}=\sqrt{\ \dfrac{1}{1\ 032\times4,0\cdot{10}^{-10}}\ }\)
\(\color{blue}c_\mathrm{liquide4}=1\ 556\ \mathrm{m.s^{-1}}\)
Question⚓
Q6. Calculer la vitesse de propagation d'un son dans chaque solide du document 7.
Solution⚓
A3-Q6.
\(c_{solide}=\sqrt{\ \dfrac{E}{\rho}\ }\)
\(c_{acier1}=\sqrt{\ \dfrac{210\cdot{10}^9}{7\ 500}}=5\ 292\ \mathrm{m.s^{-1}}\)
\(c_{acier2}=\sqrt{\ \dfrac{210\cdot{10}^9}{8\ 100}}=5\ 092\ \mathrm{m.s^{-1}}\)
\(c_{beton1}=\sqrt{\ \dfrac{20\cdot{10}^9}{2\ 200}}=3\ 015\ \mathrm{m.s^{-1}}\)
\(c_{beton2}=\sqrt{\ \dfrac{40\cdot{10}^9}{2\ 200}}=4\ 264\ \mathrm{m.s^{-1}}\)
\(c_{brique1}=\sqrt{\ \dfrac{14\cdot{10}^9}{1\ 900}}=2\ 714\ \mathrm{m.s^{-1}}\)
\(c_{brique2}=\sqrt{\ \dfrac{14\cdot{10}^9}{2\ 100}}=2\ 582\ \mathrm{m.s^{-1}}\)
\(c_{verre}=\sqrt{\ \dfrac{69\cdot{10}^9}{2\ 530}}=5\ 222\ \mathrm{m.s^{-1}}\)
\(c_{ps1}=\sqrt{\ \dfrac{2,8\cdot{10}^9}{1\ 040}}=1\ 641\ \mathrm{m.s^{-1}}\)
\(c_{ps2}=\sqrt{\ \dfrac{3,4\cdot{10}^9}{1\ 040}}=1\ 808\ \mathrm{m.s^{-1}}\)
\(c_{ps3}=\sqrt{\ \dfrac{2,8\cdot{10}^9}{1\ 060}}=1\ 625\ \mathrm{m.s^{-1}}\)
\(c_{ps4}=\sqrt{\ \dfrac{3,4\cdot{10}^9}{1\ 060}}=1\ 791\ \mathrm{m.s^{-1}}\)
Question⚓
Q7. Comparer les résultats précédents et conclure.
🚩 Définitions (à savoir)⚓
Q8. Compléter les phrases des définitions suivantes :
📌 Les autres grandeurs physiques qui caractérisent un son⚓
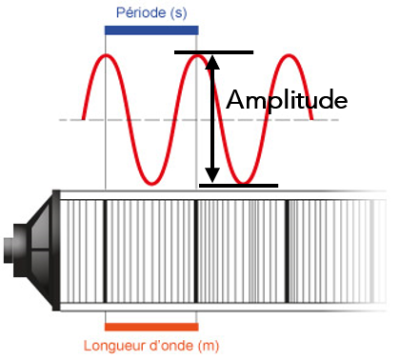
Complément : Document n°8 : Caractéristiques d’une onde périodique
Un son est une onde (une déformation, une information) qui se répète de manière régulière, pendant un certain temps. On dit alors que l’onde est périodique.
Une onde sonore (comme toute onde), est caractérisée par une amplitude, une longueur d'onde, une période.
Complément : Document n°9 : L’amplitude d’un son
L’amplitude d’un son se rapporte à son intensité ou à sa puissance. Nous ressentons directement cette « amplitude » lorsque nous percevons un son ; en effet lorsqu’un son est qualifié de « fort » et qu’il nous semble « puissant » à l’écoute, c’est que son onde est ample.
Pour mesurer l’amplitude d’une onde sonore, on mesure la variation de pression entre la compression et la dépression maximale du milieu de propagation.
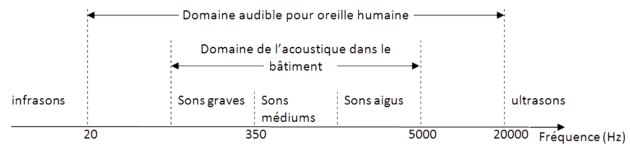
Complément : Document n°10 : Domaine audible
Le domaine de l’audible de l’Homme se situe entre \(20\ \mathrm{Hz}\) et \(20\ 000\ \mathrm{Hz}\) (ce domaine se rétrécit avec l'âge) mais nous ne produisons pas, avec la voix, des fréquences supérieures à \(1\ 000\ \mathrm{Hz}\).
❔ Quelques questions⚓
Question⚓
Q9. Quelles sont les grandeurs physiques caractérisant une onde (sonore) présentées dans le Doc.n°8 ? En donner une définition.
Solution⚓
A3-Q9.
Les grandeurs physiques qui caractérisent une onde (sonore) sont la période, l'amplitude et la longueur d’onde.
La période est la durée séparant deux répétitions.
La longueur d’onde est la distance parcourue par l’onde pendant une période.
L'amplitude est l'intensité (ou puissance) de l'onde.
Question⚓
Écrire la réponse à la question suivante dans la zone de définition ci-dessous.
Q10. Comment appelle-t-on le nombre de fois qu'un phénomène périodique se reproduit par unité de mesure du temps ? Donner la formule la calculant ainsi que les unités des grandeurs.
Solution⚓
A3-Q10.
Le nombre de fois qu'un phénomène périodique se reproduit par unité de mesure du temps se nomme la fréquence.
Définition :
Question⚓
Écrire la réponse à la question suivante dans la zone de définition ci-dessous.
Q11. En partant de la définition de la longueur d’onde, donner la relation qui la relie à la fréquence et à sa célérité.
Solution⚓
A3-Q11.
La longueur d’onde est la distance que parcourt l’onde en une période, on a alors l’expression de la célérité :
\(c=\dfrac{\lambda}{T}=\lambda\times f\)
Définition :
Question⚓
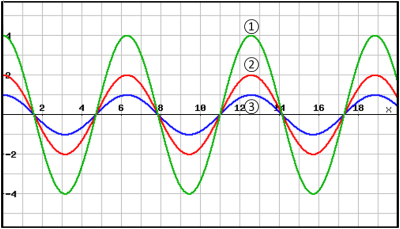
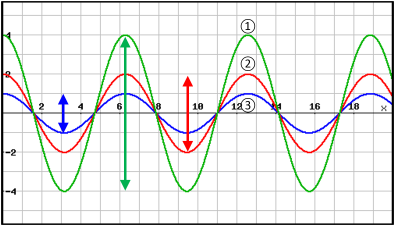
Q12. Représenter et donner la valeur des amplitudes (sans unité dans cet exemple) des trois signaux suivants. Puis classer les signaux par ordre de puissance.
L’unité de l’amplitude dépend de l’onde utilisée et de l’appareil de mesure utilisé. On trouve fréquemment les unités suivantes : le volt \(\mathrm{V}\), le mètre \(\mathrm{m}\).
Solution⚓
A3-Q12.
L’amplitude du signal (1) est de 8, celle du signal (2) de 4, et celle su signal (3) de 2.
Par ordre de puissance : (3) < (2) < (1).
- 1 Amplitude du signal (1)
Elle vaut 8 carreaux.
- 2 Amplitude du signal (2)
Elle vaut 4 carreaux.
- 3 Amplitude du signal (3)
Elle vaut 2 carreaux.
🏋️♂️ Exercices⚓
💪 Exercice n°1⚓
Un télémètre est un appareil de mesure permettant de mesurer des distances.
Question⚓
Q16. En imaginer le principe de fonctionnement.
Solution⚓
A3-Q16.
Le télémètre va émettre une onde dont on connait la vitesse qui va aller se réfléchir sur l’objet dont on cherche à déterminer la distance qui le sépare de nous.
L’onde va alors revenir vers le télémètre qui va mesurer la durée de l’aller-retour et pouvoir calculer la distance entre le télémètre et l’objet.
Question⚓
La distance entre le télémètre (laser) et la cible est de \(5\ \mathrm{m}\). Sachant que la vitesse c de la lumière est de \(3,00\cdot{10}^8\ \mathrm{m.s^{-1}}\), déterminer le temps mis par la lumière pour effectuer l’aller-retour.
Q17. Quelle caractéristique d’un télémètre le rendra plus précis dans ses mesures ?
Question⚓
Q18. La fréquence de l’horloge d’un télémètre est de \(100\ \mathrm{GHz}\). Cela signifie que la durée la plus courte mesurable correspond à la période de l’horloge. En déduire la précision/erreur sur la mesure d’une distance.
Solution⚓
A3-Q18.
La période de cette horloge est : \(T=\dfrac{1}{f}=\dfrac{1}{100\cdot{10}^9}={10}^{-11}\ \mathrm{s}=10\ \mathrm{ps}\)
La durée la plus courte mesurable est donc de \(10\ \mathrm{ps}\). La distance minimale mesurable sera alors de :
\(d=c\times T=3,00\cdot{10}^8\times{10}^{-11}=3,00\cdot{10}^{-3}\ \mathrm{m}=3,00\ \mathrm{mm}\)
Question⚓
Les télémètres optiques sont parfois remplacés par des télémètres à ultrasons. L’onde ultrasonore émise se propage à la vitesse du son dans l’air environnant, soit \(342\ \mathrm{m/s}\). Nous souhaitons une précision au \(\mathrm{cm}\).
Q19. Quelle fréquence minimale d’horloge devra-t-on choisir dans ce télémètre ?
Question⚓
Q20. Le son a une vitesse de \(343\ \mathrm{m/s}\) à \(20\ \mathrm{^\circ C}\) et de \(331\ \mathrm{m/s}\) à \(0\ \mathrm{^\circ C}\), ceci influence la mesure de manière significative. Expliquer ce qu’il faudra donc effectuer comme réglage sur un télémètre à ultrasons.
💪 Exercice n°2⚓
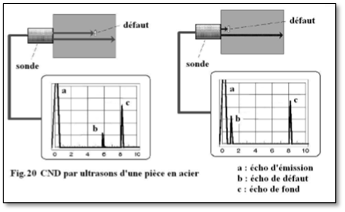
Les ultrasons sont utilisés dans de nombreux domaines et dans de multiples applications. Ils peuvent permettre entre autres de mettre en évidence des défauts dans une pièce, une paroi, mais également aussi de déterminer l’épaisseur d’une cloison. Ces différentes techniques sont basées sur les phénomènes de réflexion et de transmission (réfraction) d’une onde lorsqu’elle change de milieu de propagation.
Question⚓
Q21. En vous aidant d’internet, définir (avec vos mots à vous) les phénomènes de réflexion et de transmission d’une onde sonore lorsqu’elle change de milieu de propagation. Un schéma peut avantageusement compléter l’explication.
Question⚓
Q22. Commenter la situation ci-dessus. La sonde d’ultrasons s’appelle également un palpeur.
Solution⚓
A3-Q22.
La sonde envoi des ultrasons sur une pièce en acier. Il y a un écho démission qui correspond à la face en contact avec la sonde, et un écho de fond qui correspond à la face opposée de la pièce en acier. S’il y a un défaut, on aura un écho supplémentaire entre celui d’émission et celui de fond qui permettra de savoir où se trouve le défaut.
Question⚓
Q23. Deux échos sont mesurés avec un intervalle de temps de \(2,9\cdot{10}^{-6}\ \mathrm{s}\) dans un mur en béton. En déduire la largeur de la faille.
Données : \(c_\text{béton}=3\ 000\ \mathrm{m.s^{-1}}\)