📄 Documents⚓
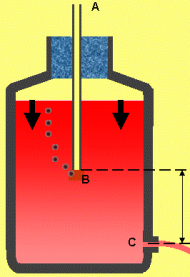
Complément : Présentation du dispositif expérimental - [Document n°1]
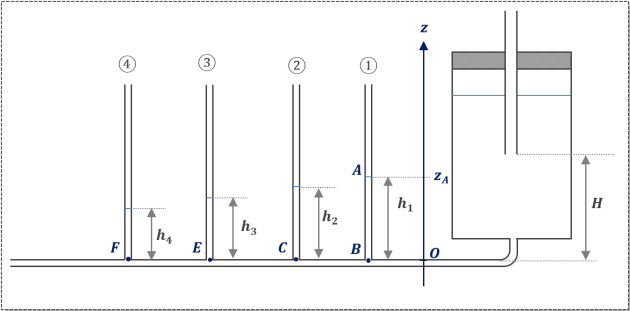
Quatre tubes verticaux, équidistants, sont soudés sur une canalisation horizontale de diamètre constant.
Un vase génère un écoulement stationnaire (le débit constant).
On peut faire varier le débit d'écoulement en modifiant la hauteur entre l'extrémité du tube plongeant (B) et la canalisation horizontale (C).
Petite vidéo de l'expérience : 01 - Act.n°4 - VIDEO - Dispositif-debit-pression-volume.mp4 
Complément : Observations - [Document n°2]
👨🎓 Questionnement⚓
Question⚓
Q1. (ANA/RÉA) En vous aidant du schéma ci-dessous, expliquer comment chacun des 4 tubes verticaux permet de mesurer la pression qui règne en un point de la canalisation horizontale. Donner l'expression littérale de la pression relative en ces points de la canalisation horizontale.
Solution⚓
A4-Q1.
Si on prend le tube ①, la hauteur de montée d'eau \(h_1\) nous permet de déterminer une variation de pression entre le niveau de l'eau (point A) et le point de la canalisation au niveau du tube ① (point B).
Comme on connaît la valeur de la pression au point A (c'est la pression atmosphérique), et que la hauteur \(h_1\) ne varie pas, on peut déterminer à l'aide de la relation fondamentale de l'hydrostatique la pression absolue au point B dans la canalisation horizontale :
Si on définit un axe des altitudes tel que \(z_\mathrm{B}=0\) et \(z_\mathrm{A}=h_1\), alors on a : \(p_\mathrm{B}=p_\mathrm{Atm}+\rho\cdot g\cdot h_1\)
Ceci est une pression absolue. Ce qui nous intéresse est la pression relative dans la canalisation, c'est-à-dire :
\[\fbox{$ {\Large {\color{blue} \text{ } p_\mathrm{B_{\, rel}} = \rho \cdot g \cdot h_1 \text{ } } } $}\] car \(\large p_\mathrm{rel}=p_\mathrm{abs}-p_\mathrm{atm}\).
On a donc ainsi de la même manière :
\({\Large {\color{blue} \text{ } p_\mathrm{C_{\, rel}} = \rho \cdot g \cdot h_2 \text{ } } }\)
\({\Large {\color{blue} \text{ } p_\mathrm{E_{\, rel}} = \rho \cdot g \cdot h_3 \text{ } } }\)
\({\Large {\color{blue} \text{ } p_\mathrm{F_{\, rel}} = \rho \cdot g \cdot h_4 \text{ } } }\)
Question⚓
Q2. (ANA/COM) Expliquer comment ces expériences permettent de décrire l'évolution de la pression le long d'une canalisation horizontale.
Question⚓
Q3. (ANA/COM) Le phénomène observé s'appelle pertes de charge régulières. Selon vous à quoi est-il dû ?
Question⚓
Q4. (ANA/COM) D'après les deux expériences menées, de quels paramètres dépend ce phénomène ?
🏋️♂️ Entraînement à l'utilisation du diagramme de Moody⚓
Question⚓
Q5. (ANA/RÉA) En vous appuyant sur les documents fournis en annexe (clic droit, ouvrir dans un nouvel onglet), estimer les pertes de charge entre les deux extrémités d'une canalisation horizontale, en tube de PVC, de diamètre \(100\ \mathrm{mm}\), et de longueur \(50,0\ \mathrm{m}\), transportant de l'eau à \(10\ \mathrm{^\circ C}\), avec pour vitesse moyenne d'écoulement \(2,00\ \mathrm{m.s^{-1}}\).
Aide : Calculer le nombre de Reynolds \(Re\) pour la situation. Puis utiliser le diagramme de Moody pour déterminer le coefficient de frottement f (il faudra déterminer la rugosité relative de la canalisation). Et enfin calculer les pertes de charges \(\Delta P\).
Réponses à trouver : \(Re=1,53 \cdot{10}^5\) , \(f \approx 0,0175\), \(\Delta P \approx1,75\cdot{10}^4\ \mathrm{Pa}\)
Question⚓
Q6. (ANA/RÉA) Même question pour une canalisation en fonte, puis en fonte goudronnée.
Aide : Même raisonnement qu'à la question précédentes, mais déterminer la valeur minimale du coefficient de frottement. ; Réponses : \(Re=1,53\cdot{10}^5\) , \(f_{fonte}\approx0,025\), \(\Delta P_{fonte}\approx2,50\cdot{10}^4\ Pa\)
\(f_{fonte\ goud}\approx0,022\), \(\Delta P_{fonte\ goud}\approx2,20\cdot{10}^4\ Pa\)
Question⚓
Q7. (ANA/RÉA) Estimer les pertes de charge pour \(50\ \mathrm{m}\) d'une canalisation horizontale en PVC, de diamètre \(200\ \mathrm{mm}\), transportant de l'eau à \(5\ \mathrm{^\circ C}\), avec une vitesse moyenne d'écoulement de \(0,100\ \mathrm{m.s^{-1}}\).
Aide : Même raisonnement qu'à la question précédentes. ; Réponses : \(Re=1,32\cdot{10}^4\) , \(f_{PVC}\approx0,030\), \(\Delta P_{PVC}\approx37,5\ Pa\) .
Conseil :
On peut calculer via ce site internet le coefficient de frottement et le nombre de Reynolds en entrant la viscosité cinématique, la rugosité, le diamètre de la canalisation et la vitesse du fluide : http://www.lmnoeng.com/moody.php