Activité n°4 : Force des acides et de bases - [Chapitre : Les réactions acido-basiques]

Titre de l'activité : Activité n°4 : Force des acides et de bases - [Chapitre : Les réactions acido-basiques]

Durée : 2h

Compétences

ANA - Exploiter ses connaissances, les informations extraites ou les résultats obtenus
ANA - Élaborer une démarche
APP - Rechercher et extraire l'information
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
APP - Mobiliser les connaissances en rapport avec le problème
RÉA - Calculer, utiliser une formule
RCO - Restituer des connaissances

Notions

Connaître l'expression du pH d'une solution aqueuse. Connaître son étendue.
Calculer le pH d'une solution aqueuse dans des cas simples (solutions acide et basique).
Identifier un acide (fort/faible) et une base (forte/faible) de Brönsted.
Exploiter les diagrammes de prédominance.
Identifier l'espèce prédominante d'un couple acide-base connaissant le pH du milieu et le pKa du couple.
À l'aide d'un diagramme de répartition obtenu par simulation, déterminer le pourcentage en acide et en base d'un couple acide – base à un pH donné.
Écrire l'équation chimique d'une réaction acide-basique et exprimer la constante d'acidité, les couples étant donnés.

👨‍🎓 Les acides forts ⚓

Définition :

Certains acides $AH$, appelés acides forts, réagissent totalement avec l'eau en libérant des ions oxonium $H_3O_{\left(aq\right)}^+$ suivant l'équation : $AH+H_2O_{\left(\ell\right)}\ \longrightarrow\ \ A_{\left(aq\right)}^-+\ H_3O_{\left(aq\right)}^+$
L'acide $AH$ n'existe donc pas dans l'eau : il est sous la forme d'ion $A_{\left(aq\right)}^-$ et d'ion oxonium $H_3O_{\left(aq\right)}^+$.

Cette équation doit être écrite avec une simple flèche $\longrightarrow$ pour indiquer que la réaction est totale.

Question⚓

Q1. Écrire les équations modélisant l'apparition des ions oxonium $H_3O_{\left(aq\right)}^+$ lors de la réaction des acides forts ci-dessous avec l'eau :

Le chlorure d'hydrogène $HC\ell_{\left(g\right)}$ :
L'acide nitrique $HNO_{3\ \left(\ell\right)}$ :
L'acide perchlorique $HC\ell O_{4\ \left(\ell\right)}$ :

Solution ⚓

A4-Q1.

Le chlorure d'hydrogène $HC\ell_{\left(g\right)}$ : $HC\ell_{\left(g\right)}+H_2O_{\left(\ell\right)}\ \longrightarrow \ H_3O_{\left(aq\right)}^++C\ell_{\left(aq\right)}^-$
L'acide nitrique $HNO_{3\ \left(\ell\right)}$ : $HNO_{3\ \left(\ell\right)}+H_2O_{\left(\ell\right)}\ \longrightarrow \ H_3O_{\left(aq\right)}^++NO_{3\ \left(aq\right)}^-$
L'acide perchlorique $HC\ell O_{4\ \left(\ell\right)}$ : $HC\ell O_{4\ \left(\ell\right)}+H_2O_{\left(\ell\right)}\ \longrightarrow \ H_3O_{\left(aq\right)}^++C\ell O_{4\ \left(aq\right)}^-$

Question⚓

Q2. On fait réagir $n\ \mathrm{mol}$ d'un acide fort noté $AH$ avec de l'eau en excès. Le volume total de la solution obtenue est noté $V$. Donner l'expression littérale de la concentration $C_A$ de l'acide $AH$.

Solution ⚓

A4-Q2.

Comme l'acide a totalement réagit avec l'eau, on a : $C_A=\dfrac{n}{V}$

Question⚓

Q3. Donner l'expression littérale de la concentration en ion oxonium $\Big[H_3O^+\Big]$ à l'état final (une fois que la réaction est terminée).

Solution ⚓

A4-Q3.

Comme tous les $AH$ se sont transformés en ions $H_3O^+$ et en $A^-$, on a donc : $\Big[H_3O^+\Big]_f=\dfrac{n}{V}=C_A$

Question⚓

Q4. Donner l'expression littérale de la valeur du pH de la solution en fonction de $C_A$.

Solution ⚓

A4-Q4.

$pH=-\log{{\ \left[H_3O^+\right]}_f}\ \ \ \ \Longleftrightarrow\ \ \ \mathbf{pH=-\log\ {C_A}}$

Définition : Conclusion (À SAVOIR)

Un acide $AH$ est fort si sa réaction avec l'eau est totale : $AH+H_2O_{\left(\ell\right)}\ \longrightarrow\ \ A_{\left(aq\right)}^-+\ H_3O_{\left(aq\right)}^+$

Pour une solution d'acide fort de concentration $C_A$ : ${\fcolorbox{red}{white}{$\color{blue}\mathbf{pH=-\log\ C_A}$}}$.

👨‍🎓 Les bases fortes ⚓

Définition :

Certaines bases $AH$, appelées bases fortes, réagissent totalement avec l'eau en libérant des ions hydroxyde $HO_{\left(aq\right)}^-$ suivant l'équation : $B^-+H_2O_{\left(\ell\right)}\ \longrightarrow\ \ BH_{\left(aq\right)}+\ HO_{\left(aq\right)}^-$
La base $B^-$ n'existe donc pas dans l'eau ; elle est sous la forme $BH$ et d'ion hydroxyde $HO_{\left(aq\right)}^-$.

Une base forte $XHO_{\left(s\right)}$ peut aussi libérer des ions hydroxyde $HO_{\left(aq\right)}^-$ par sa dissolution totale dans l'eau suivant l'équation : $XHO_{\left(s\right)}\ \longrightarrow\ X_{\left(aq\right)}^++\ HO_{\left(aq\right)}^-$
Cette équation doit être écrite avec une simple flèche $\longrightarrow$ pour indiquer que la réaction est totale.

Question⚓

Q5. Écrire les équations modélisant l'apparition des ions hydroxyde $HO_{\left(aq\right)}^-$ lors de la réaction des bases fortes ci-dessous avec l'eau :

L'ion amidure $NH_{2\ \left(aq\right)}^-$ :
L'ion méthylate $CH_3O_{\left(aq\right)}^-$ :
La soude $NaOH_{\left(s\right)}$ (hydroxyde de sodium) :

Solution ⚓

A4-Q5.

L'ion amidure $NH_{2\ \left(aq\right)}^-$ : $NH_{2\ \left(aq\right)}^-+H_2O_{\left(\ell\right)}\rightarrow NH_{3\ \left(aq\right)}+HO_{\left(aq\right)}^-$
L'ion méthylate $CH_3O_{\left(aq\right)}^-$ : $CH_3O_{\left(aq\right)}^-+H_2O_{\left(\ell\right)}\rightarrow CH_3OH_{\left(aq\right)}+HO_{\left(aq\right)}^-$
La soude $NaOH_{\left(s\right)}$ (hydroxyde de sodium) : $NaOH_{\left(s\right)}\rightarrow Na_{\left(aq\right)}^++\ HO_{\left(aq\right)}^-$

Question⚓

Q6. (RÉA) On fait réagir $\mathrm{mol}$ d'une base forte noté $B^-$ avec de l'eau en excès. Le volume total de la solution obtenue est noté $V$. Donner l'expression littérale de la concentration $C_B$ de la base $B^-$ .

Solution ⚓

A4-Q6.

Comme la base a totalement réagit avec l'eau, on a : $C_B=\dfrac{n}{V}$

Rappel :

À $25\mathrm{^\circ C}$, on a : $K_e=\left[H_3O^+\right] \times \left[HO^-\right]=1,0\cdot{10}^{-14}$

$\log{\frac{A}{B}}=\log{A}-\log{B}$

Question⚓

Q7. Donner l'expression littérale de la concentration en ion oxonium $\Big[HO^+\Big]$ à l'état final (une fois que la réaction est terminée).

Données :

Solution ⚓

A4-Q7.

$\Big[HO^-\Big]_f=\dfrac{n}{V}=C_B$

Question⚓

Q8. Donner l'expression littérale de la valeur du $pH$ de la solution en fonction de $C_B$.

Données :

Solution ⚓

A4-Q8.

$pH=-\log{{\ \left[H_3O^+\right]}_f}$

$pH=-\log{\frac{K_e}{\left[HO^-\right]}}$

$pH=-\log{K_e}+\log{C_B}$

$\color{blue}\mathbf{pH=pK_e+\log{C_B}}$ avec $\mathbf{pK_e=14}$

Définition : Conclusion (À SAVOIR)

Une base $B^-$ est forte si sa réaction avec l'eau est totale : $B^-+H_2O_{\left(\ell\right)}\ \longrightarrow\ \ BH_{\left(aq\right)}+\ HO_{\left(aq\right)}^-$

Pour une solution de base forte de concentration $C_B$ : ${\fcolorbox{red}{white}{$\color{blue}\mathbf{pH=pK_e+\log{C_B}}$}}$.

👨‍🎓 Réaction entre un acide fort et une base forte ⚓

Définition :

La réaction entre un acide fort et une base forte est une réaction totale d'équation :

$H_3O_{\left(aq\right)}^+\ +\ HO_{\left(aq\right)}^-\ \longrightarrow\ 2\ H_2O_{\left(\ell\right)}$

Cette réaction qui peut libérer beaucoup d'énergie thermique (exothermique) et doit être réalisée avec précaution.

💪 Exercice n°1 ⚓

Un volume $V=5,0\ \mathrm{mL}$ d'une solution aqueuse $S$ d'hydroxyde de sodium (base forte) de concentration

$c=1,5\cdot{10}^{-3}\ \mathrm{mol.L^{-1}}$ est versé dans un volume $V^\prime=20\ \mathrm{mL}$ d'une solution aqueuse $S^\prime$ d'acide chlorhydrique (acide fort) de concentration $c^\prime=7,5\cdot{10}^{-4}\ \mathrm{mol.L^{-1}}$.

Question⚓

Q9. Calculer le $pH$ de $S$ et $S^\prime$.

Réponse à trouver : pH de 11 pour $S$, et pH de 3,1 pour $S^\prime$.

Solution ⚓

A4.Q9.

$pH\left(S\right)=pK_e+\log{\ c}=-\log{{10}^{-14}}+\log{\ \left(1,5\cdot{10}^{-3}\right)}=11$

$pH\left(S^\prime\right)=-\log{\ c^\prime}=-\log{\ \left(7,5\cdot{10}^{-4}\right)}=3,1$

Question⚓

Q10. Écrire l'équation de la réaction qui a lieu.

Solution ⚓

A4.Q10.

$H_3O_{\left(aq\right)}^+\ +\ HO_{\left(aq\right)}^-\ \longrightarrow\ 2\ H_2O_{\left(\ell\right)}$

Question⚓

Q11. La réaction est-elle totale ? Justifier.

Solution ⚓

A4.Q11.

La réaction est totale car il s'agit de la réaction entre une base forte (la soude) et un acide fort (l'acide chlorhydrique).

Question⚓

Q12. Calculer la quantité de matière n d'ions hydroxyde $HO_{\left(aq\right)}^-$ apportée par $S$ et celle $n^\prime$ d'ions oxonium $H_3O_{\left(aq\right)}^+$ apportée par $S^\prime$.

Aide :

La concentration molaire $C$ et la quantité de matière $n$ sont reliées par la formule : $C=\dfrac{n}{V}$ où $V$ est le volume de la solution.

Réponse à trouver : $n=7,5\cdot{10}^{-6}\ \mathrm{mol}$ et $n^\prime = 1,5\cdot{10}^{-5}\ \mathrm{mol}$

Solution ⚓

A4.Q12.

$n=c\times V=1,5\cdot{10}^{-3}\times5,0\cdot{10}^{-3}=7,5\cdot{10}^{-6}\ \mathrm{mol}$

$n^\prime=c^\prime\times V^\prime=7,5\cdot{10}^{-4}\times20\cdot{10}^{-3}=1,5\cdot{10}^{-5}\ \mathrm{mol}$

Comme les coefficients stœchiométriques^[*] sont de 1 pour les deux réactifs, cela signifie qu'un ion oxonium réagit avec un ion hydroxyde. Si on continue ce raisonnement, $1\ \mathrm{mol}$ d'ions oxonium réagit avec $1\ \mathrm{mol}$ d'ions hydroxyde.

Question⚓

Q13. Compte tenu de ce qui précède, calculer la quantité de matière du réactif en excès (celui pour lequel il en reste à la fin).

Réponse à trouver : $\left(n_{H_3O^+}\right)_{restant}=7,5\cdot{10}^{-6}\ \mathrm{mol}$

Solution ⚓

A4.Q13.

Comme il s'agit d'une réaction 1 pour 1, le réactif en excès est celui pour lequel la quantité de matière est la plus grande, donc c'est $H_3O^+$ qui est en excès.

Il va alors rester :

$\left(n_{H_3O^+}\right)_{restant}=n^\prime - n =1,5\cdot{10}^{-5} -7,5\cdot{10}^{-6}=7,5\cdot{10}^{-6}\ \mathrm{mol}$

Question⚓

Q14. Comment appelle-t-on le réactif qui a été totalement consommé ?

Solution ⚓

A4.Q13.

Le réactif qui a été totalement consommé durant la transformation chimique s'appelle le réactif limitant.

Définition : Conclusion (À SAVOIR)

Le réactif en excès est le réactif qui a été introduit en trop grosse quantité : il n'a pas été totalement consommé, il en reste donc encore à la fin de la transformation chimique.
Le réactif limitant est le réactif qui a été introduit en trop faible quantité : il a été totalement consommé durant la transformation chimique, et donc n'est plus présent à la fin.

👨‍🎓 Les acides faibles et les bases faibles ⚓

Définition : Les réactions partielles

Certains acides $AH$, appelés acides faibles, réagissent partiellement avec l'eau suivant l'équation :
$AH+H_2O_{\left(\ell\right)}\ \rightleftarrows\ A_{\left(aq\right)}^-+\ H_3O_{\left(aq\right)}^+$
Certaines bases $B^-$, appelées bases faibles, réagissent partiellement avec l'eau suivant l'équation :
$B^-+H_2O_{\left(\ell\right)}\ \rightleftarrows\ BH_{\left(aq\right)}+\ HO_{\left(aq\right)}^-$

À la fin de la réaction, les réactifs et les produits sont simultanément présents. Une réaction partielle (ou limitée) conduit à un état d'équilibre.

Ces équations doivent être écrites avec une double flèche $\rightleftarrows$ pour indiquer que les réactions sont partielles.

Complément : Document n°1 : La constante d'acidité

Soit un couple acide-base faible $AH_{\left(aq\right)}\ / \ A_{\left(aq\right)}^-$ associé à la réaction d'équation : $AH_{\left(aq\right)}+H_2O_{\left(\ell\right)}\ \rightleftarrows \ A_{\left(aq\right)}^-+\ H_3O_{\left(aq\right)}^+$

On définit une grandeur $K_a$ sans unité appelée constante d'acidité telle que :

\[{\fcolorbox{red}{white}{$ {\ \ \ \mathbf{K_a=\dfrac{\Big[A^-\Big]\times \Big[H_3O^+\Big]}{\Big[AH\Big]}} \ \ \ } $}} \]

Il est d'usage de poser : ${\fcolorbox{blue}{white}{$\mathbf{pK_a=-\log{\ K_a}}$}}$

Où :

$\mathbf{K_a}$ : Constante d'acidité (sans unité)
$\mathbf{\Big[H_3O^+\Big]}$ : concentration en ion oxonium $\left(\mathrm{mol.L^{-1}}\right)$
$\mathbf{\Big[A^-\Big]}$ : concentration de la forme basique $\left(\mathrm{mol.L^{-1}}\right)$
$\mathbf{\Big[AH\Big]}$ : concentration de la forme acide $\left(\mathrm{mol.L^{-1}}\right)$

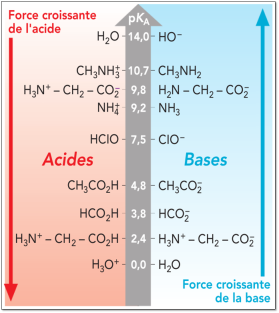
Plus le $pK_a$ du couple est grand (ou plus la constante d'acidité est petite), moins l'acide se dissocie dans l'eau.

En effet, plus $\Big[AH\Big]$ est grand par rapport à $\Big[A^-\Big]$ , plus la constante $K_a$ est petite. Ainsi, plus le $pK_a$ d'un acide est grand, plus cet acide est faible.

Complément : Document n°2 : Valeurs de pKa à 25°C

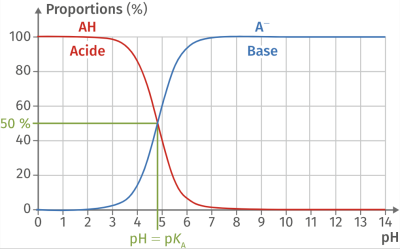
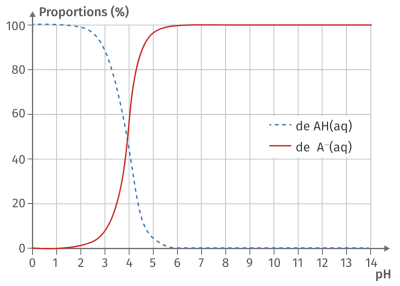
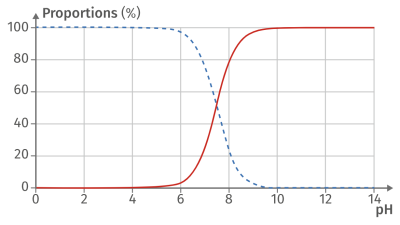
Complément : Document n°3 : Diagramme de distribution

Le diagramme de distribution d'un couple acide-base montre la répartition des deux formes acide et basique d'un couple acide-base en fonction du pH.

Pour $\mathbf{pH=pK_a}$, les deux formes sont en quantités égales.

Attention : Pas de malentendu

Lorsqu'une réaction est limitée, on dit qu'elle atteint un état d'équilibre. Attention, cet état d'équilibre est dynamique, c'est-à-dire que la réaction directe et la réaction inverse se produisent simultanément, à la même vitesse.
Raisonner sur la constante d'acidité ou sur le $pK_a$ amène à la même conclusion. L'une se base sur des puissances de 10 négatives tandis que l'autre est comprise entre 0 et 14 dans l'eau.
La dangerosité d'un acide n'est pas liée à sa force, mais à sa concentration en solution.

Complément : Supplément numérique 🎥

Vous pouvez visionner cette vidéo (clic ici) sur la constante d'acidité (ou QR-Code).

Lien : https://p-berger.canoprof.fr/eleve/Ressources/VIDEO-Constante-acidite.mp4

(Source : C Ciachera sur youtube)

Question⚓

Q15. D'après le document 2, quel(le) est...

...l'acide le plus fort dans l'eau ?
...la base la plus forte dans l'eau ?

Solution ⚓

A4-Q15.

L'acide le plus fort dans l'eau est l'ion oxonium $H_3O^+$.
La base la plus forte dans l'eau est l'ion hydroxyde $HO^-$.

Question⚓

Q16. D'après la définition du $K_a$ dans le Doc.1, établir l'expression littérale du $pH$ d'une solution d'acide faible $AH_{\left(aq\right)}$ en fonction de son $pK_a$, de sa concentration $\Big[AH\Big]$ et de la concentration de sa base conjuguée $\Big[A^-\Big]$.

Solution ⚓

A4-Q16.

\[\begin{array}{rcl} \large{ K_a=\dfrac{\Big[A^-\Big] \times \Big[H_3O^+\Big] }{ \Big[AH\Big] }} & \Longleftrightarrow & \large {\Big[H_3O^+\Big] = \dfrac{K_a \times \Big[AH\Big] }{ \Big[A^-\Big] }} \\ & \Longrightarrow & \large {pH=-\log {\left(\ \dfrac{K_a \times \Big[AH\Big] }{ \Big[A^-\Big] } \ \right) }} \\ & \Longrightarrow & \large {pH= -\log K_a - \log {\left(\ \dfrac{ \Big[AH\Big] }{ \Big[A^-\Big] } \ \right) }} \\ \\ & \Longrightarrow & {\fcolorbox{red}{white}{$ {\large {\color{red} pH= pK_a - \log { \dfrac{ \Big[AH\Big] }{ \Big[A^-\Big] } } } }$}} \large\hspace{10mm} \textsf{ou}\hspace{10mm} {\fcolorbox{blue}{white}{$ {\large {\color{blue} pH= pK_a + \log { \dfrac{ \Big[A^-\Big] }{ \Big[AH\Big] } } } }$}} \end{array} \]

Question⚓

Q17. Que peut-on dire de la concentration de l'acide faible $\Big[AH\Big]$ et de sa base conjuguée $\Big[A^-\Big]$ lorsque $pH=pK_a$ ?

Aide : utiliser le rappel ci-contre →

$\Large{\color{blue}\textsf{Rappels sur les log :}} \\ \\\large{\color{black}\begin{array}{ll}\log{\ (A\times B)}=\log{A}+\log{B} \ \ \ \ &\log{1}=0 \\\textsf{si } x<1 \textsf{ alors } \log{x}<0 & \textsf{si } x>1 \textsf{ alors } \log{x}>0\end{array}}$

Solution ⚓

A4-Q17.

$pH=pK_a$, on a :
\[\begin{array}{rcl} {-\log{\ \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}}=0 } & \Longleftrightarrow & { \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}=1 } \\ \\ & \Longleftrightarrow & {\fcolorbox{red}{white}{$ \hspace{2mm} {\mathbf{\color{red} \Big[AH\Big]=\Big[A^-\Big] } } \hspace{2mm} $}} \end{array} \]

Question⚓

Q18. Que peut-on dire de la concentration de l'acide faible $\Big[AH\Big]$ et de sa base conjuguée $\Big[A^-\Big]$ lorsque $pH>pK_a$ ?

Q19. Que peut-on dire de la concentration de l'acide faible $\Big[AH\Big]$ et de sa base conjuguée $\Big[A^-\Big]$ lorsque $pH<pK_a$ ?

Solution ⚓

A4-Q18.

$pH>pK_a$, on a :

\[\begin{array}{rcl} {pK_A -\log{\ \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}}> pK_a } & \Longleftrightarrow & { pK_a - pK_a > \log{\ \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}} } \\ & \Longleftrightarrow & { 0 > \log{\ \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}} } \\ & \Longleftrightarrow & { \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}} < 1 \\ \\ & \Longleftrightarrow & {\fcolorbox{red}{white}{$ \hspace{2mm} {\mathbf{\color{red} \Big[AH\Big]<\Big[A^-\Big] } } \hspace{2mm} $}} \end{array} \]

A4-Q19.

$pH<pK_a$, on a :

\[\begin{array}{rcl} {pK_A -\log{\ \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}}< pK_a } & \Longleftrightarrow & { pK_a - pK_a < \log{\ \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}} } \\ & \Longleftrightarrow & { 0 < \log{\ \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}} } \\ & \Longleftrightarrow & { \dfrac{\Big[AH\Big]}{\Big[A^-\Big]}} > 1 \\ \\ & \Longleftrightarrow & {\fcolorbox{red}{white}{$ \hspace{2mm} {\mathbf{\color{red} \Big[AH\Big]>\Big[A^-\Big] } } \hspace{2mm} $}} \end{array} \]

Question⚓

Ces informations se résument sur un diagramme appelé diagramme de prédominance.

Q20. Compléter alors le diagramme de prédominance ci-dessous :

Aide : il faut indiquer quelle forme prédomine en fonction de la valeur du $pH$ de la solution (et par rapport à la valeur du $pK_a$ du couple.

Solution ⚓

A4-Q20.

Définition : Conclusion (À SAVOIR)

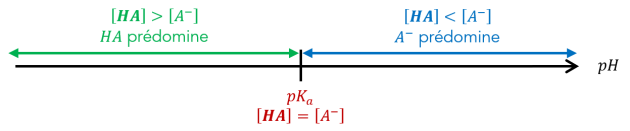
Le diagramme de prédominance montre graphiquement les espèces d'un couple acide-base qui sont majoritairement prédominantes à une valeur de $\mathbf{pH}$ donnée.

Quand le $pH$ est égale au $pK_a$ d'un couple, les concentrations de la forme acide et de la forme basique de ce couple sont égales.
Lorsque le pH est inférieur au $pK_a$, la forme acide prédomine.
Lorsque le pH est supérieur au $pK_a$, la forme basique prédomine.

\[{\fcolorbox{red}{white}{$ {\Large \ \ \ \mathbf{ pH=pK_a + \log{\ \dfrac{\Big[A^-\Big]}{\Big[AH\Big]}} } \ \ \ } $}} \]

🏋️‍♂️ Exercices ⚓

💪 Exercice n°2 :⚓

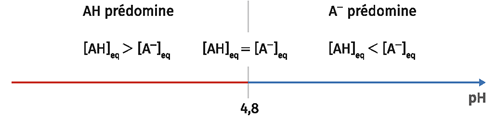
Le $pK_a$ du couple acide éthanoïque / ion éthanoate que l'on notera $AH\ / \ A^-$ vaut 4,8.

Question⚓

Q21. Tracer le diagramme de prédominance de ce couple en faisant apparaître les zones où les espèces $AH$ et $A^-$ prédomine, et aussi les comparaisons des concentrations en ces deux espèces.

Solution ⚓

A4-Q21.

💪 Exercice n°3 : Couple acide lactique/ion lactate ⚓

L'acide lactique est un acide qui peut se trouver dans le lait, le vin ou même certains fruits et légumes. Le diagramme de distribution du couple acide lactique / ion lactate (notés $AH_{\left(aq\right)}$ et $A_{\left(aq\right)}^-$ est représenté ci-contre.

Question⚓

Q22. Déterminer graphiquement le $pH$ pour lequel $\Big[AH\Big]=\Big[A^-\Big]$.

Solution ⚓

A4-Q22.

Graphiquement, on lit $\Big[AH\Big]=\Big[A^-\Big]$ pour $pH = 4$.

Question⚓

Q23. Déterminer le $pK_a$ du couple.

Solution ⚓

A4-Q23.

Lorsque $pH = pK_a$, alors : $\Big[AH\Big]=\Big[A^-\Big]$.

Ainsi, le $pK_a$ du couple vaut 4.

Question⚓

Q24. Déterminer les proportions des deux formes acide et basique pour $pH=3,0$.

Solution ⚓

A4-Q24.

On peut voir graphiquement que, pour $pH = 3,0$, il y a environ $90 \%$ de forme acide et $10 \%$ de forme basique.

Question⚓

Q25. Utiliser les résultats de la question précédente pour déterminer à nouveau le $pK_a$. Comparer cette nouvelle valeur calculée à celle déterminée graphiquement à la question Q23.

Aide : il faut utiliser les % des proportions des deux espèces par rapport à la concentration totale, et utiliser la relation entre le pH et le pKa.

Solution ⚓

A4-Q25.

D'après la question précédente :

$\Big[AH\Big]=0,90\times C_{totale}$

$\Big[A^-\Big]=0,10\times C_{totale}$

$\Big[H_3O^+\Big]=10^{-pH}=10^{-3}\ \mathrm{mol.L^{-1}}$

Ainsi : $K_a=\dfrac{\Big[A^-\Big]\times \Big[H_3O^+\Big]}{\Big[AH\Big]}=\dfrac{0,10\times C_{totale}\times 10^{-3}}{0,90\times C_{totale}}=1,1\cdot 10^{-4}$

On a donc : $pK_a=-\log \ K_a=-\log {\ \left(\ 1,1\cdot 10^{-4}\ \right) }=3,9586...\approx 4$

On retrouve bien la valeur du $pK_a$ déterminée graphiquement précédemment.

💪 Exercice n°4 : Acide hypochloreux/ion hypochlorite ⚓

Les ions hypochlorite, $C\ell O_{\left(aq\right)}^-$, entrent dans la composition de l'eau de Javel. Ils ont pour acide conjugué l'acide hypochloreux $HC\ell O_{\left(aq\right)}$.

Diagramme de distribution

Question⚓

Q26. D'après le diagramme de distribution, déterminer le $pH$ où $\Big[HC\ell O\Big]=\Big[C\ell O^-\Big]$ .

Solution ⚓

A4-Q26.

Graphiquement, on lit $\Big[HC\ell O\Big]=\Big[C\ell O^-\Big]$ pour $pH \approx 7,5$.

Question⚓

Q27. En déduire le $pK_a$ du couple $HC\ell O_{\left(aq\right)} \ / \ C\ell O_{\left(aq\right)}^-$.

Solution ⚓

A4-Q27.

Lorsque $pH = pK_a$, alors $\Big[HC\ell O\Big]=\Big[C\ell O^-\Big]$.

D'après la question précédente, on peut dire que $pK_a\approx 7,5$.

Question⚓

Q28. Attribuer chacune des courbes du diagramme.

Solution ⚓

A4-Q28.

Lorsque $pH < pK_a$ la forme acide prédomine, donc la courbe verte en pointillés correspond au taux de forme acide $HC\ell O_{\left(aq\right)}$.

La courbe rouge en trait plein correspond au taux de forme basique $C\ell O_{\left(aq\right)}^-$.

Question⚓

Q29. Tracer le diagramme de prédominance.

Solution ⚓

A4-Q29.

Question⚓

Q30. Déterminer le $pH$ pour lequel on a $\Big[HC\ell O\Big]=2\times \Big[C\ell O^-\Big]$.

Solution ⚓

A4-Q30.

On doit avoir : $\Big[C\ell O^-\Big]\approx 33,333... \%$ et $\Big[HC\ell O\Big]\approx 66,666... \%$

On lit graphiquement $pH\approx 7,0$.

Une tolérance est appliquée sur la valeur déterminée graphiquement vu que le graphique n'est pas super précis au niveau des graduations...