Activité n°5 {Exp.} : Mesure d'une constante d'acidité - [Chapitre : Les réactions acido-basiques]

Titre de l'activité : Activité n°5 {Exp.} : Mesure d'une constante d'acidité - [Chapitre : Les réactions acido-basiques]

Durée : 1h

Matériels de l'élève

Une solution notée $AH$ d'acide éthanoïque $CH_3COOH_{\left(aq\right)}$ de concentration $C_{AH}=1,0\cdot{10}^{-1}\ mol.L^{-1}$
Une solution notée $A^-$ d'ions éthanoate $CH_3COO_{\left(aq\right)}^-$ de concentration $C_{A^-}=1,0\cdot{10}^{-1}\ mol.L^{-1}$
2 burettes graduées de $25\ \mathrm{mL}$
Un pH-mètre et ses solutions tampons ($pH=4$ et $7$)
Un bécher $100\ \mathrm{mL}$
Un agitateur magnétique et son barreau

Compétences

ANA - Exploiter ses connaissances, les informations extraites ou les résultats obtenus
ANA - Élaborer une démarche
APP - Rechercher et extraire l'information
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
APP - Mobiliser les connaissances en rapport avec le problème
RÉA - Calculer, utiliser une formule
RCO - Restituer des connaissances

Notions

Identifier un acide (fort/faible) et une base (forte/faible) de Brönsted.
Identifier l'espèce prédominante d'un couple acide-base connaissant le pH du milieu et le pKa du couple.
Écrire l'équation chimique d'une réaction acide-basique et exprimer la constante d'acidité, les couples étant donnés.

Complément : Document n°1 : La constante d'acidité

Soit un couple acide-base faible $AH_{\left(aq\right)}\ / \ A_{\left(aq\right)}^-$ associé à la réaction d'équation : $AH_{\left(aq\right)}+H_2O_{\left(\ell\right)}\ \rightleftarrows \ A_{\left(aq\right)}^-+\ H_3O_{\left(aq\right)}^+$

On définit une grandeur $K_a$ sans unité appelée constante d'acidité telle que :

\[{\fcolorbox{red}{white}{$ {\ \ \ \mathbf{K_a=\dfrac{\Big[A^-\Big]\times \Big[H_3O^+\Big]}{\Big[AH\Big]}} \ \ \ } $}} \]

Il est d'usage de poser : ${\fcolorbox{blue}{white}{$\mathbf{pK_a=-\log{\ K_a}}$}}$

Où :

$\mathbf{K_a}$ : Constante d'acidité (sans unité)
$\mathbf{\Big[H_3O^+\Big]}$ : concentration en ion oxonium $\left(\mathrm{mol.L^{-1}}\right)$
$\mathbf{\Big[A^-\Big]}$ : concentration de la forme basique $\left(\mathrm{mol.L^{-1}}\right)$
$\mathbf{\Big[AH\Big]}$ : concentration de la forme acide $\left(\mathrm{mol.L^{-1}}\right)$

Plus le $pK_a$ du couple est grand (ou plus la constante d'acidité est petite), moins l'acide se dissocie dans l'eau.

En effet, plus $\Big[AH\Big]$ est grand par rapport à $\Big[A^-\Big]$ , plus la constante $K_a$ est petite. Ainsi, plus le $pK_a$ d'un acide est grand, plus cet acide est faible.

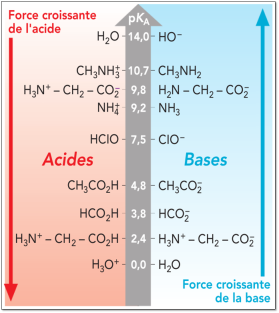
Complément : Document n°2 : Valeurs de pKa à 25°C

Méthode : Protocole expérimental

Remplir la 1ère burette de la solution d'acide éthanoïque.
Ajuster le zéro et vérifier l'absence de bulle d'air au niveau du robinet.
Remplir la 2ème burette de la solution d'ions éthanoate.
Ajuster le zéro et vérifier l'absence de bulle d'air au niveau du robinet.
Placer un bécher sous les deux burettes.
Adapter l'agitateur magnétique sous le bécher et placer le barreau aimanté.
En utilisant judicieusement les burettes, réaliser les mélanges donnés dans le tableau ci-dessous et mesurer la valeur du pH pour chacun d'eux.
Bien garder l'agitation constante.

Tableau de valeurs (à compléter)

$V_{AH}\ \left(\ \mathrm{mL}\ \right)$	$25,0$	$25,0$	$25,0$	$25,0$
$V_{A^-}\ \left(\ \mathrm{mL}\ \right)$	$5,0$	$10,0$	$20,0$	$25,0$
$pH$
$\dfrac{V_{A^-}}{V_{AH}}$
$\log \left( \dfrac{V_{A^-}}{V_{AH}}\right)$

$V_{AH}\ \left(\ \mathrm{mL}\ \right)$	$20,0$	$10,0$	$5,0$
$V_{A^-}\ \left(\ \mathrm{mL}\ \right)$	$25,0$	$25,0$	$25,0$
$pH$
$\dfrac{V_{A^-}}{V_{AH}}$
$\log \left( \dfrac{V_{A^-}}{V_{AH}}\right)$

Question⚓

Q1. Écrire la réaction acido-basique de l'acide éthanoïque sur l'eau.

Solution ⚓

A5-Q1.

$CH_3COOH_{\left(aq\right)}+H_2O_{\left(\ell\right)}\ \rightleftarrows\ CH_3COO_{\left(aq\right)}^-+H_3O_{\left(aq\right)}^+$

On peut la noter aussi (en abrégé) : $AH_{\left(aq\right)}+H_2O_{\left(\ell\right)}\ \rightleftarrows\ A_{\left(aq\right)}^-+H_3O_{\left(aq\right)}^+$

Question⚓

Q2. En s'aidant du Doc.1, déduire l'expression du $pH$ en fonction du $pK_a$.

$\large{\color{blue}\textsf{Rappels sur les log :}} \\ \\\large{\color{black}\begin{array}{ll}\log{\ (A\times B)}=\log{A}+\log{B} \ \ \ \ &\log{1}=0 \\\textsf{si } x<1 \textsf{ alors } \log{x}<0 & \textsf{si } x>1 \textsf{ alors } \log{x}>0\end{array}}$

Solution ⚓

A5-Q2.

$pK_a=-\log{\ K_a}$

$pK_a=-\log{\dfrac{\Big[A^-\Big]\cdot\Big[H_3O^+\Big]}{\left[AH\right]}}$

$pK_a=-\log{\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}}-\log{\ \Big[H_3O^+\Big]}$

$pK_a=pH-\log{\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}}$

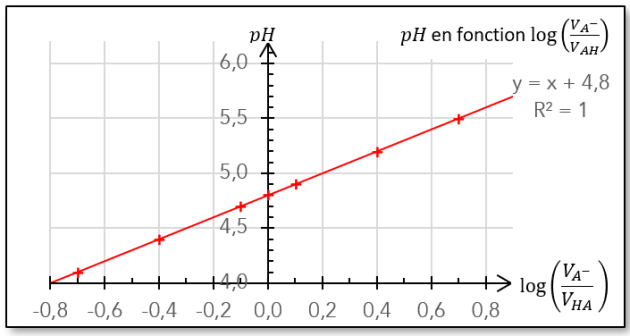
$\color{blue}\mathbf{pH=pK_a+\log{\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}}}$

Question⚓

Q3. Exprimer littéralement la concentration en acide $\Big[AH\Big]$ dans le mélange, en considérant qu'aucune réaction ne se produit. (Aucun calcul numérique ne doit être réalisé ici...)

Solution ⚓

A5-Q3.

$\color{blue}\Big[AH\Big]=\dfrac{n_{AH}}{V_{tot}}\ \ \ \ \Longleftrightarrow\ \ \ \ \ \mathbf{\color{red}\Big[AH\Big]=\dfrac{C_{AH}\times V_{AH}}{V_{AH}+V_{A^-}}}$

Question⚓

Q4. Démontrer alors l'égalité : $\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}=\dfrac{V_A}{V_{AH}}$.

Solution ⚓

A5-Q4.

$\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}=\dfrac{\ \ \dfrac{C_{A^-}\times V_{A^-}}{V_{AH}+V_{A^-}}\ \ }{\dfrac{C_{AH}\times V_{AH}}{V_{AH}+V_{A^-}}}$

$\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}=\dfrac{C_{A^-}\times V_{A^-}}{V_{AH}+V_{A^-}}\times\dfrac{V_{AH}+V_{A^-}}{C_{AH}\times V_{AH}}$

$\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}=\dfrac{C_{A^-}\times V_{A^-}}{C_{AH}\times V_{AH}}$

$\Longleftrightarrow \color{red}\mathrm{\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}= \dfrac{V_{A^-}} {V_{AH}} }$ car $C_{A^-}=C_{AH}=1,0\cdot{10}^{-1}\ \mathrm{mol.L^{-1}}$

Question⚓

Q5. En utilisant le tableur de Regressi, calculer les valeurs des rapports des deux dernières lignes du tableau de valeur : $\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}$ et $\log \dfrac{\Big[A^-\Big]}{\Big[AH\Big]}$.

Question⚓

Q6. Tracer alors la courbe $pH=f\left(\log{\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}}\right)$ montrant l'évolution du pH en fonction de $\log{\dfrac{\Big[A^-\Big]}{\Big[AH\Big]}}$.

La modéliser et l'imprimer.

Solution ⚓

A5-Q6.

Question⚓

Q7. En déduire la valeur de la constante d'acidité $K_a$ du couple $CH_3COOH_{\left(aq\right)}\ / \ CH_3COO_{\left(aq\right)}^-$.

Solution ⚓

A5-Q7.

Lorsque $\log{\left(\dfrac{V_{A^-\ }}{V_{HA}}\right)}=0$ on a avec la relation $\left(1\right) : pH=pK_a$.

Donc grâce à la courbe et à son ordonnée à l'origine, on obtient : $pK_a=4,8$.

\(V_{AH}\ \left(\ \mathrm{mL}\ \right)\)	\(25,0\)	\(25,0\)	\(25,0\)	\(25,0\)
\(V_{A^-}\ \left(\ \mathrm{mL}\ \right)\)	\(5,0\)	\(10,0\)	\(20,0\)	\(25,0\)
\(pH\)
\(\dfrac{V_{A^-}}{V_{AH}}\)
\(\log \left( \dfrac{V_{A^-}}{V_{AH}}\right)\)

\(V_{AH}\ \left(\ \mathrm{mL}\ \right)\)	\(20,0\)	\(10,0\)	\(5,0\)
\(V_{A^-}\ \left(\ \mathrm{mL}\ \right)\)	\(25,0\)	\(25,0\)	\(25,0\)
\(pH\)
\(\dfrac{V_{A^-}}{V_{AH}}\)
\(\log \left( \dfrac{V_{A^-}}{V_{AH}}\right)\)

Complément : Document n°1 : La constante d'acidité

Complément : Document n°2 : Valeurs de pKa à 25°C

Méthode : Protocole expérimental

Tableau de valeurs (à compléter)

Question⚓

Solution⚓

Question⚓

Solution⚓

Question⚓

Solution⚓

Question⚓

Solution⚓

Question⚓

Question⚓

Solution⚓

Question⚓

Solution⚓

Solution ⚓

Solution ⚓

Solution ⚓

Solution ⚓

Solution ⚓

Solution ⚓