🚩 Généralités⚓
Complément : [Document n°1] - Qu'est-ce que la viscosité ?
La viscosité d'un fluide caractérise la capacité d'un fluide à s'écouler, elle est principalement due à l'interaction entre les molécules constituant le fluide.
Pour un fluide parfait, les molécules glissent les unes sur les autres sans interactions, il n'y a donc pas de frottement, la viscosité est nulle.
Pour un fluide réel, la viscosité existe (non nulle) et traduit l'apparition de frottements, ce qui a pour effet de dissiper une partie de l'énergie transportée par le fluide sous la forme de chaleur. Une partie de l'énergie est perdue au fur et à mesure de l'écoulement, ce qui entraîne des pertes de vitesse ou de pression.
Complément : [Document n°2] - Énergie d'un fluide en mouvement
Un fluide en mouvement possède de l'énergie :
sous forme d'énergie cinétique (due à sa vitesse) : \(\large \frac{1}{2} \times \rho \times \mathrm{v}^2\)
sous forme d'énergie potentielle de pesanteur : \(\large \rho \times g \times z\)
sous forme de travail (énergie interne dû aux forces de pression) : \(\large p\) (pression)
Cette énergie peut varier lors de la circulation du fluide dans une canalisation :
à cause des frottements sur les parois de la canalisation ou entre les particules de fluide (viscosité non nulle) (à l'origine des pertes de charge, que l'on étudiera plus tard)
parce qu'une machine a été introduite sur le trajet du fluide :
une pompe va apporter de l'énergie au fluide
une turbine va prélever de l'énergie au fluide
👨🎓 Équation de Bernoulli dans le cas d'un fluide parfait en mouvement⚓
Complément : [Document n°3] - Énergie d'un fluide parfait en mouvement
Pour un écoulement stationnaire (caractérisé par des grandeurs qui sont constantes au cours du temps et en chaque point du fluide (mais peuvent être différentes entre deux points différents du fluide)) d'un fluide incompressible (la masse volumique \(\large \rho\) du fluide est constante) et parfait (sans viscosité donc pas de frottement entre particules de fluide et avec la paroi de la canalisation), un bilan d'énergie sur le fluide circulant entre deux points A et B d'une canalisation, permet d'écrire la loi de conservation de l'énergie :
En l'absence de machine :
où :
\(\large p\) est pression du fluide au point considéré, exprimée en \(\mathrm{Pa}\)
\(\large \rho\) est masse volumique du fluide, exprimée en \(\mathrm{kg.m^{-3}}\)
\(\large z\) est l'altitude du fluide, exprimée en \(\mathrm{m}\)
\(\large \mathrm{v}\) est vitesse moyenne du fluide, exprimée en \(\mathrm{m.s^{-1}}\)
\(\large g\) est l'intensité de la pesanteur telle que \(g=9,81 \ \mathrm{N.kg^{-1}}\) ou en \(\mathrm{m.s^{-2}}\)
Chacun des termes est homogène à une pression (en \(\mathrm{Pa}\)) ou à une énergie volumique (en \(\mathrm{J.m^{-3}}\) ).
En présence de machine :
où :
\(\large W_\mathrm{AB}\) est le travail volumique (exprimé en \(\mathrm{J.m^{-3}}\)), en valeur algébrique, échangé par la présence de la machine :
Avec :
\(Q_{\mathrm{V}}\) : Débit volumique du fluide en \(\mathrm{m^{3}.s^{-1}}\)
\(P_{u}\) : Puissance utile de la machine en \(\mathrm{W}\)
\(\large W_\mathrm{AB}>0\) dans le cas d'une pompe : L'énergie en B (après) est supérieure (grâce à la pompe) à l'énergie en A (avant).
\(\large W_\mathrm{AB}<0\) dans le cas d'une turbine : L'énergie en B (après) est plus petite (à cause de la turbine qui transforme une partie de l'énergie mécanique du fluide en énergie électrique) à l'énergie en A (avant).
Question⚓
Q1. (RÉA) Transformer l'équation de Bernoulli dans le cas d'un fluide immobile, sans apport d'énergie externe. Commenter la nouvelle équation obtenue.
Solution⚓
A6-Q1.
Dans le cas d'un fluide immobile, \(\mathrm{v_A}=0\) et sans apport d'énergie externe \(W_\mathrm{AB}=0\), donc on a :
\(\large p_\mathrm{A} + \rho \times g \times z_\mathrm{A} = p_\mathrm{B} + \rho \times g \times z_\mathrm{B}\)
C'est la loi fondamentale de l'hydrostatique, ce qui est logique puisque dans ce cas le fluide est immobile, donc statique.
💪 Appliquer la loi de conservation pour un fluide parfait
Faire les exercices suivants.
🏋️♂️ Exercice n°1 : Écoulement permanent à travers un ajustage⚓
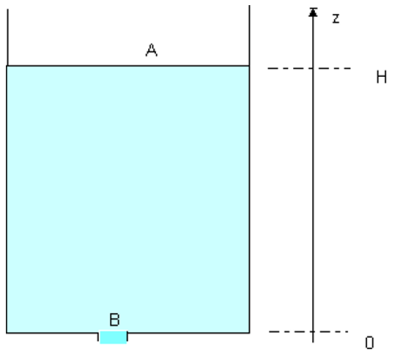
On utilise en travaux pratiques une cuve verticale (voir schéma ci-contre) remplie d'eau ; on supposera que le niveau A dans la cuve est constant. Le fluide s'écoule par un trou de diamètre D situé dans le fond de la cuve. L'eau sera considérée comme un fluide parfait incompressible.
Données numériques :
\(H=0,82\ \mathrm{m}\) ; \(D=2,0\ \mathrm{cm}\)
Masse volumique de l'eau \(\rho=1\ 000\ \mathrm{kg.m^{-3}}\)
\(g=9,81\ \mathrm{m.s^{-2}}\)
Pression atmosphérique normale \(p_0=10^5 Pa\)
Question⚓
Q2. (RÉA) Appliquer la relation de Bernoulli entre les points A et B et déterminer l'expression littérale de la vitesse \(\mathrm{v_B}\) au niveau du trou.
Aide : Penser aux simplifications avec ce qui est nul et ce qui est de même valeur.
Réponse : \(\mathrm{v_B}=\sqrt{\ 2 \times g \times H\ }\)
Solution⚓
A6-Q2.
Comme le niveau A est considéré comme constant, on peut considérer que \(\large \mathrm{v_A}\approx 0\). Comme l'eau s'écoule dans l'air par le trou en B, on a \(\large p_{\mathrm{B}}=p_{\mathrm{0}}=p_{\mathrm{A}}\).
\(\large p_{\mathrm{B}}+\rho \times g \times z_{\mathrm{B}}+\dfrac{1}{2} \times \rho \times \mathrm{v_B}^2\ = \ p_{\mathrm{A}}+\rho\times g\times z_{\mathrm{A}}+\dfrac{1}{2} \times \rho \times \mathrm{v_A}^2\)
Comme \(\large \mathrm{v_A}=0\) et \(z_{\mathrm{A}}=H\) et \(z_{\mathrm{B}}=0\) d'après le schéma :
\(\large p_{\mathrm{0}}+\dfrac{1}{2} \times \rho \times \mathrm{v_B}^2\ =p_{\mathrm{0}}+\rho\times g\times H\)
\(\large \dfrac{1}{2} \times \rho \times \mathrm{v_B}^2=\rho \times g\times H\)
\(\large \dfrac{1}{2} \times \mathrm{v_B}^2=g\times H\)
\(\large \color{blue} \mathrm{v_B}=\sqrt{\ 2 \times g \times H\ }\)
Question⚓
Q4. (RÉA) Calculer numériquement la vitesse \(\large \mathrm{v_B}\) et le débit-volume \(\large q_{\mathrm{V}}\) au point B.
Réponse : \(\mathrm{v_B}=4\ \mathrm{m.s^{-1}}\) et \(q_{\mathrm{V}}=1,3\ \mathrm{L.s^{-1}}\)
Solution⚓
A6-Q4.
\(\large \mathrm{v_B}=\sqrt{\ 2\times9,81\times0,82\ }\)
\(\large \color{blue} \mathrm{v_B}=4,0\ \mathrm{m.s^{-1}}\)
\(\large q_{\mathrm{V}}=\pi\times\dfrac{\left(2,0\cdot{10}^{-2}\right)^2}{4}\times4,0\)
\(\large\color{blue} q_{\mathrm{V}}=1,3\cdot{10}^{-3}\ \mathrm{m^{3}.s^{-1}} \;\;\;\; =1,3\ \mathrm{L.s^{-1}}\)
🏋️♂️ Exercice n°2 : Cavitation dans une conduite⚓
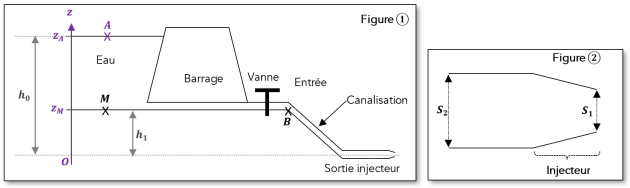
L'eau d'un lac artificiel, retenue par un barrage de montagne, alimente une centrale hydroélectrique située à la sortie d'une canalisation (figure 1 ci-dessous).
La canalisation, de section constante \(S_2\), se termine par un injecteur schématisé (figure 2 ci-dessus). La section de sortie de l'injecteur est \(S_1\). On se propose d'étudier le rôle de l'injecteur.
On donne l'équation de Bernoulli pour un fluide parfait incompressible en écoulement permanent :
\(p+\rho\times g\times z+\dfrac{1}{2}\times\rho\times\mathrm{v}^2=Cste\) On négligera la variation du niveau d'eau du lac au cours de l'écoulement.
Complément : Données numériques :
Les altitudes sont mesurées en prenant comme référence la sortie de la canalisation
\(h_0=100\ \mathrm{m}\) ; \(h_1=60\ \mathrm{m}\)
Les sections de la canalisation sont : \(S_2=3\ \mathrm{m^2}\) et \(S_1=2\ \mathrm{m^2}\)
Masse volumique de l'eau \(\rho=1\ 000\ \mathrm{kg.m^{-3}}\)
\(g=9,81\ \mathrm{m.s^{-2}}\)
Pression atmosphérique normale \(p_0=10^5 Pa\)
Question⚓
Q5. (RÉA) La vanne située à la sortie du barrage est fermée. Déterminer la pression en un point M situé au fond du lac.
Aide : Pourquoi peut-on utiliser le principe fondamental de l'hydrostatique ?
Réponse : \(p_{\mathrm{M}}=4,92\cdot{10}^5\ \mathrm{Pa}\)
Solution⚓
A6-Q5.
Comme la vanne est fermée, on peut appliquer le principe fondamental de l'hydrostatique entre M et A :
\(\large p_\mathrm{M}+\rho\times g\times z_M=p_\mathrm{A}+\rho\times g\times z_\mathrm{A}\) Avec \(\large z_\mathrm{M}=h_1=60\ \mathrm{m}\) et \(\large z_\mathrm{A}=h_0=100\ \mathrm{m}\)
\(\large p_\mathrm{M}=p_\mathrm{A}+\rho\times g\times z_\mathrm{A}-\rho\times g\times z_\mathrm{M}\) Et \(\large p_\mathrm{A}=p_0\) étant la pression atmosphérique.
\(\large p_\mathrm{M}=p_0+\rho\times g\times\left(\ z_\mathrm{A}-z_\mathrm{M}\ \right)\)
\(\large p_\mathrm{M}={10}^5+1\ 000\times9,81\times\left(100-60\right)\)
\(\large \color{blue} p_\mathrm{M}=4,92\cdot{10}^5\ \mathrm{Pa}\)
La vanne est maintenant ouverte. À la sortie de la canalisation, l'eau s'écoule dans l'air.
Question⚓
Q6. (RÉA) Montrer que la vitesse de l'eau à la sortie de l'injecteur est \(\mathrm{v}_1=44,3\ \mathrm{m.s^{-1}}\). On prendra \(z_1=0\ \mathrm{m}\).
Aide : Utiliser l'équation de Bernoulli entre deux points bien choisis, il est possible de le faire de deux manières différentes.
Solution⚓
A6-Q6.
L'eau s'écoule dans l'air, donc la pression en sortie d'injecteur est la pression atmosphérique, on a donc : \(\large p_1=p_0=p_\mathrm{A}\)
Comme la vanne est ouverte, on peut appliquer l'équation de Bernoulli entre A et la sortie de l'injecteur :
\(\large p_{\mathrm{A}}+\rho\ g\ z_{\mathrm{A}}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2=p_{\mathrm{1}}+\rho\ g\ z_{\mathrm{1}}+\dfrac{1}{2} \ \rho \ \mathrm{v_1}^2\)
Comme la surface libre du barrage est très grande par rapport à l'ouverture de l'injecteur, on aura \(\large \mathrm{v_A}\approx 0\).
\(\large \rho\ g\ z_{\mathrm{A}}=\rho\ g\ z_{\mathrm{1}}+\dfrac{1}{2} \ \rho \ \mathrm{v_1}^2\)
\(\large \mathrm{v_1}^2=2\times g\ \left(z_{\mathrm{A}}-z_1\right)\)
\(\large \mathrm{v_1}=\sqrt{\ 2\ g\ \left(z_{\mathrm{A}}-z_1\right) \ }\)
\(\large \mathrm{v_1}=\sqrt{\ 2\times9,81\times\left(100-0\right)\ }\)
\(\large \color{red} \mathrm{v_1}=44,3\ \mathrm{m.s^{-1}}\)
Autre méthode en utilisant l'équation de Bernoulli entre M et la sortie de l'injecteur :
\(p_{\mathrm{M}}+\rho\ g\ z_{\mathrm{M}}+\dfrac{1}{2} \ \rho \ \mathrm{v_M}^2=p_{\mathrm{1}}+\rho\ g\ z_{\mathrm{1}}+\dfrac{1}{2} \ \rho \ \mathrm{v_1}^2\)
Au point M, on considérera que la hauteur d'eau ne variera pas, on aura donc \(p_{\mathrm{M}}=4,92\cdot{10}^5\ Pa\), de plus la vitesse de l'eau au fond du barrage sera nulle : \( \mathrm{v_M}\approx 0\).
\(\dfrac{1}{2} \ \rho \ \mathrm{v_1}^2 = p_{\mathrm{M}} - p_{\mathrm{1}} +\rho\ g\ z_{\mathrm{M}}-\rho\ g\ z_{\mathrm{1}}\)
\(\mathrm{v_1}^2 =2\times \dfrac{p_{\mathrm{M}} - p_{\mathrm{1}} +\rho\ g \ z_{\mathrm{M}} }{\rho}\)
\(\mathrm{v_1}^2 =2\times \left( \dfrac{p_{\mathrm{M}} - p_{\mathrm{1}}}{\rho} + g \ z_{\mathrm{M}} \right)\)
\(\mathrm{v_1} =\sqrt{ \ 2\times \left( \dfrac{p_{\mathrm{M}} - p_{\mathrm{1}}}{\rho} + g \ z_{\mathrm{M}} \right) \ }\)
\(\mathrm{v_1} =\sqrt{2\times\left(\dfrac{4,92\cdot{10}^5-{10}^5}{1\ 000}+9,81\times60\right)}\)
\(\color{cyan} \mathrm{v_1} =44,3\ \mathrm{m.s^{-1}}\)
Question⚓
Q7. (RÉA) Calculer le débit massique \(Q_\mathrm{m1}\) de l'eau.
Réponse : \(Q_\mathrm{m1}=8,86\cdot{10}^4\ \mathrm{kg.s^{-1}}\)
Question⚓
Q8. (RÉA) En utilisant l'équation de continuité, calculer la vitesse\(\large \mathrm{v_2}\) de l'eau en un situé juste avant l'injecteur. Que peut-on dire de cette vitesse en d'autres points de la canalisation ?
Aide : Utiliser l'équation de continuité.
Réponse : \(\mathrm{v_2}=29,5\ \mathrm{m.s^{-1}}\)
Solution⚓
A6-Q8.
Équation de continuité : \(\large S_1\times \mathrm{v}_1=S_2\times \mathrm{v}_2\)
\(\large \mathrm{v}_2=\mathrm{v}_1\times\dfrac{S_1}{S_2}=44,3\times\dfrac{2}{3}\color{blue}=29,5\ \mathrm{m.s^{-1}}\)
La vitesse en d'autres points de cette canalisation sera la même car le diamètre de la canalisation ne variera pas, et qu'on a \(\mathrm{v}\times S=Cste\)
Question⚓
Q9. (RÉA) Déterminer l'altitude \(h^\prime\), de l'entrée de la canalisation au point B (juste après la vanne) pour laquelle la pression en ce point s'annulerait.
Aide : Utiliser l'équation de Bernoulli.
Réponse : \(h^{\prime}=65,8\ \mathrm{m}\)
Solution⚓
A6-Q9.
On veut ici \(\large p_{\mathrm{B}}=0\), on applique donc l'équation de Bernoulli entre B et A avec \(\large \mathrm{v}_A\approx0\) et \(\large p_{\mathrm{A}}=p_0\) et \(\mathrm{v_B}=\mathrm{v}_2=29,5\ \mathrm{m.s^{-1}}\)
\(\large p_{\mathrm{B}}+\rho\ g\ z_{\mathrm{B}}+\dfrac{1}{2} \ \rho \ \mathrm{v_B}^2=p_{\mathrm{A}}+\rho\ g\ z_{\mathrm{A}}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2\)
\(\large\rho\ g\ h^\prime=p_0+\rho\ g\ z_{\mathrm{A}}-\dfrac{1}{2}\ \rho\ \mathrm{v_B}^2\)
\(\large h^\prime=\dfrac{p_0}{\rho\times g}+\ z_{\mathrm{A}}-\frac{1}{2} \times \dfrac{\mathrm{v_B}^2}{g}\)
\(\large h^\prime=\dfrac{{10}^5}{1\ 000\times9,81}+100-\frac{1}{2}\times\dfrac{{29,5}^2}{9,81}\)
\(\large \color{blue} h^\prime=65,8\ \mathrm{m}\)
On supprime l'injecteur.
Question⚓
Q11. (RÉA) Quelle est la vitesse \(\mathrm{v}\) à la sortie de la canalisation ?
Aide : Quels sont les changements dans les valeurs fournies ?
Réponse : \(\mathrm{v}=44,3\ \mathrm{m.s^{-1}}\)
Question⚓
Q12. (RÉA) Déterminer l'altitude \(\large h^{\prime\prime}\) , de l'entrée de la canalisation pour laquelle pression s'annulerait.
Aide : Utiliser l'équation de Bernoulli.
Réponse : \(h^{\prime\prime}=10,2\ \mathrm{m}\)
Solution⚓
A6-Q12.
On veut ici \(\large p_{\mathrm{B}}=0\), on applique donc l'équation de Bernoulli entre B et A avec \(\large \mathrm{v}_A\approx0\) et \(\large p_{\mathrm{A}}=p_0\) et \(\mathrm{v_B}=\mathrm{v}_2=44,3\ \mathrm{m.s^{-1}}\)
\(\large p_{\mathrm{B}}+\rho\ g\ z_{\mathrm{B}}+\dfrac{1}{2} \ \rho \ \mathrm{v_B}^2=p_{\mathrm{A}}+\rho\ g\ z_{\mathrm{A}}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2\)
\(\large\rho\ g\ h^{\prime\prime}=p_0+\rho\ g\ z_{\mathrm{A}}-\dfrac{1}{2}\ \rho\ \mathrm{v_B}^2\)
\(\large h^{\prime\prime}=\dfrac{p_0}{\rho\times g}+\ z_{\mathrm{A}}-\frac{1}{2} \times \dfrac{\mathrm{v_B}^2}{g}\)
\(\large h^{\prime\prime}=\dfrac{{10}^5}{1\ 000\times9,81}+100-\frac{1}{2}\times\dfrac{{44,3}^2}{9,81}\)
\(\large \color{blue} h^{\prime\prime}=10,2\ \mathrm{m}\)
La pression dans une conduite ne peut pas descendre en dessous de la pression saturante vapeur du fluide en-deçà de laquelle le fluide se vaporise. Dès que la pression atteint cette valeur, il se forme des bulles de gaz résultant de la vaporisation du liquide (phénomène de cavitation). C'est un phénomène destructeur : contraintes mécaniques, corrosion...
Question⚓
Q13. (ANA) Justifier la nécessité de l'injecteur à la sortie de la canalisation.
🏋️♂️ Exercice n°3 : Relation de Bernoulli⚓
Question⚓
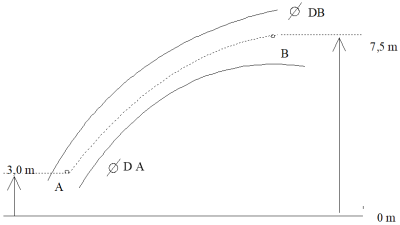
Q14. (RÉA) Calculer la pression en B (détailler les calculs littéraux, puis les applications numériques).
Aide : Appliquer l'équation de Bernoulli, en calculant les vitesses à partir des débits volumiques.
Réponse : \(p_{\mathrm{B}}=3,19\cdot{10}^4\ \mathrm{Pa}\)
Solution⚓
A6-Q14.
On applique l'équation de Bernoulli entre B et A :
\(\large p_{\mathrm{B}}+\rho\ g\ z_{\mathrm{B}}+\dfrac{1}{2} \ \rho \ \mathrm{v_B}^2=p_{\mathrm{A}}+\rho\ g\ z_{\mathrm{A}}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2\)
\(\large p_{\mathrm{B}}=p_{\mathrm{A}}+\rho\ g\ z_{\mathrm{A}}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2-\rho\ g\ z_{\mathrm{B}}-\dfrac{1}{2} \ \rho \ \mathrm{v_B}^2\)
\(\large p_{\mathrm{B}}=p_{\mathrm{A}}+\rho\ g \left( z_{\mathrm{A}} - z_{\mathrm{B}} \right) +\dfrac{1}{2} \ \rho \left( \mathrm{v_A}^2 - \mathrm{v_B}^2 \right)\)
Comme le débit se conserve, on a : \(\large \mathrm{v_A}=\dfrac{Q_{\mathrm{V}}}{S_\mathrm{A}}\) et \(\large \mathrm{v_B}=\dfrac{Q_{\mathrm{V}}}{S_\mathrm{B}}\)
\(\large \color{blue} \left(\mathrm{v_A}=3,64\ \mathrm{m/s} \mathrm{\ \ \ et\ \ \ } \ \mathrm{v_B}=1,09\ \mathrm{m/s} \right) \)
On a également : \(\large p_\mathrm{A}=0,70\ \mathrm{bar}=0,70\cdot{10}^5\ \mathrm{Pa}\)
et \(\large Q_\mathrm{V}=350\ \mathrm{L/s}=0,350\ \mathrm{m^3/s}\)
Calculons les valeurs des surfaces des sections :
\(\large S_\mathrm{A}=\pi\times\dfrac{D_\mathrm{A}^2}{4}=\pi\times\dfrac{\left(35,0\cdot{10}^{-2}\right)^2}{4}=9,62\cdot{10}^{-2}\ \mathrm{m^2}\)
\(\large S_\mathrm{B}=\pi\times\dfrac{D_\mathrm{B}^2}{4}=\pi\times\dfrac{\left(64,0\cdot{10}^{-2}\right)^2}{4}=3,22\cdot{10}^{-1}\ \mathrm{m^2}\)
\(\large p_\mathrm{B}=0,70\cdot{10}^5+1000\times9,81\times\left(3-7,5\right)+\dfrac{1}{2}\times1000\times\left(\left(\dfrac{0,350}{9,62\cdot{10}^{-2}}\right)^2-\left(\dfrac{0,350}{3,22\cdot{10}^{-1}}\right)^2\right)\)
\(\large \color{blue} p_\mathrm{B}=3,19\cdot 10^4\ \mathrm{Pa}\)
🏋️♂️ Exercice n°4 : Barrage hydroélectrique et turbine⚓
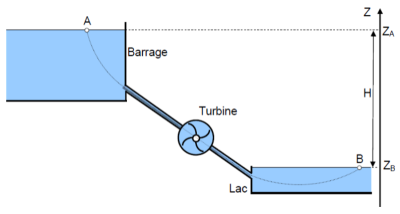
Une conduite cylindrique amène l'eau d'un barrage (dont le niveau \(\large Z_{\mathrm{A}}\) est maintenu constant) dans une turbine, elle-même reliée à un alternateur, pour fabriquer de l'électricité.
On branche à la sortie de la turbine une canalisation évacuant l'eau vers un lac.
Le niveau \(\large Z_{\mathrm{B}}\) de la surface libre du lac est supposé constant.
Le débit massique traversant la turbine est \(\large Q_{\mathrm{m}}=175\ \mathrm{kg/s}\)
On donne :
l'accélération de la pesanteur \(\large g=\ 9,8\ \mathrm{m.s^{-2}}\)
\(\large H=\left(Z_{\mathrm{A}}-Z_{\mathrm{B}}\right)=35\ \mathrm{m}\)
\(\large \rho=1\ 000\ \mathrm{kg.m^{-3}}\)
Question⚓
Q15. (RÉA) Calculer le débit volumique \(\large Q_{\mathrm{V}}\).
Aide : Quelle relation relie \(Q_{\mathrm{V}}\) et \(Q_{\mathrm{m}}\) ?
Réponse : \(Q_{\mathrm{V}}=0,175\ \mathrm{m^3/s}\)
Question⚓
Q16. (RÉA) En appliquant le théorème de Bernoulli, déterminer la puissance utile \(\large P_\mathrm{u}\) développée par la turbine. Préciser toutes les hypothèses simplificatrices.
Aide : Bien préciser les valeurs connues pour faire des simplifications. Utiliser l'équation de Bernoulli avec machine.
Réponse : \(P_\mathrm{u}=-6,0\cdot{10}^4\ \mathrm{W}\)
Solution⚓
A6-Q16.
L'équation de Bernoulli en présence d'une machine entre A et B est :
\(\large \left( \ p_\mathrm{A}+\rho\ g\ z_\mathrm{A}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2 \ \right) + W_\mathrm{AB}\ =\ p_\mathrm{B}+\rho\ g\ z_\mathrm{B}+\dfrac{1}{2} \ \rho \ \mathrm{v_B}^2\)
Avec :
\(p_\mathrm{A}=p_{atm}=p_\mathrm{B}\) car les 2 surfaces sont à l'air libre ;
\(\mathrm{v_A}\approx0\) car on maintient le niveau \(z_\mathrm{A}\) constant ;
\(\mathrm{v_B}\approx0\) car on le niveau \(z_\mathrm{B}\) est supposé constant.
Et aussi : \(W_\mathrm{AB}=\dfrac{P_\mathrm{u}}{Q_\mathrm{V}}\)
\(\large P_\mathrm{u}\) est négatif du point de vue du fluide qui perd de l'énergie donc cette puissance. Mais du point de vue de la machine (ici une turbine), cette énergie doit être comptée positivement. Donc on prend la valeur absolue de \(\large P_\mathrm{u}\).
Question⚓
Q17. (RÉA) Calculer la puissance récupérée sur l'arbre de la turbine si son rendement global est \(\large \eta=70\%\).
Aide : ne pas oublier la valeur absolue dans la définition du rendement.
Réponse : \(P_\text{récupérée}=4,2\cdot 10^4 \ \mathrm{W}\)
Solution⚓
A6-Q17.
Attention : Ici du point de vue de la machine (ici une turbine), l'énergie qu'elle absorbe est la valeur absolue de l'énergie cédée par le fluide. Donc la puissance absorbée par la turbine est \(\large \left| P_\mathrm{u}\right|\).
\(\large P_\text{récupérée}=\eta \times P_\text{absorbée} = \eta \times \left| P_\mathrm{u}\right|=0,70\times 6,0\cdot 10^4 \color{blue} =4,2\cdot 10^4 \ \mathrm{W}\)
Question⚓
Q18. (RÉA) Calculer la quantité d'énergie électrique \(\large W_\mathrm{elec}\) fabriquée si la turbine fonctionne pendant 24 h.
Aide : \(W_\mathrm{elec}\) est l'énergie électrique... Utiliser la puissance.
Réponse : \(W_\mathrm{elec}=1,0\ \mathrm{MW.h}\)
🏋️♂️ Exercice n°5 : Nappe phréatique et château d'eau⚓
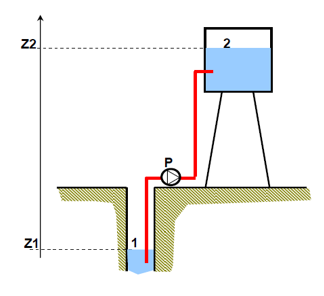
Une pompe P alimente un château d'eau à partir d'un puits à travers une conduite de diamètre \(d=150\ \mathrm{mm}\).
On donne :
les altitudes : \(\large Z_{\mathrm{2}}=26\ \mathrm{m}\), \(\large Z_{\mathrm{1}}=-5\ \mathrm{m}\)
les pressions \(\large p_1 = p_2 = 1,013\ bar\)
la vitesse d'écoulement dans la conduite : \(\large \mathrm{v}=0,4\ \mathrm{m.s^{-1}}\)
\(\large \rho=1\ 000\ \mathrm{kg.m^{-3}}\)
l'accélération de la pesanteur \(\large g=\ 9,8\ \mathrm{m.s^{-2}}\)
On négligera toutes les pertes de charge (fluide parfait).
On considérera les niveaux d'eau dans le puits et le château d'eau comme étant constants. On aura donc \(\large \mathrm{v}_1 \approx 0\) et \(\large \mathrm{v}_2 \approx 0\).
Question⚓
Q19. (RÉA) Calculer le débit volumique \(\large Q_{\mathrm{V}}\) de la pompe en \(\large \mathrm{L/s}\).
Aide : Appliquer la formule issue de l'équation de continuité.
Réponse : \(Q_\mathrm{V}=7,07\ \mathrm{L/s}\)
Solution⚓
A6-Q19.
\(\large Q_\mathrm{V}=S\times \mathrm{v}=\pi \times \dfrac{d^2}{4} \times \mathrm{v}\)
\(\large Q_\mathrm{V}=\pi \times \dfrac{ \left(150\cdot 10^{-3} \right)^2} {4} \times 0,4\)
\(\large \color{blue} Q_\mathrm{V}=7,07\cdot{10}^{-3}\ \mathrm{m^3/s}\; \; \; \; \; \; = 7,07\ \mathrm{L/s}\)
Question⚓
Q20. (RÉA) Écrire l'équation de Bernoulli entre les points 1 et 2.
Aide : Faire les simplifications.
Solution⚓
A6-Q20.
D'après l'énoncé, on a \(\large p_1 = p_2\) et \(\large \mathrm{v}_1=\mathrm{v}_2 \approx 0\).
\(\large \left(p_1+\rho\times g\times Z_1+\dfrac{1}{2}\times\rho\times\mathrm{v}^2\right)+W_{12}=p_2+\rho\times g\times Z_2+\dfrac{1}{2}\times\rho\times\mathrm{v}^2\)
\(\large p_1+\rho\times g\times Z_1+W_{12}=p_2+\rho\times g\times Z_2\)
\(\large \color{blue}\rho\times g\times Z_1+W_{12}=\rho\times g\times Z_2\)
Question⚓
Q21. (RÉA) Calculer la puissance utile \(\large P_\mathrm{utile}\) de la pompe.
Aide : isoler \(W_{12}\) dans l'équation de Bernoulli, puis utiliser sa définition.)
Réponse : \(P_\mathrm{utile}=2,15\ \mathrm{kW}\)
Solution⚓
A6-Q21.
\(\large W_{12}=\rho\times g\times\left(Z_2-Z_1\right)\) avec \(\large W_{12}=\dfrac{P_\mathrm{utile}}{Q_\mathrm{V}}\)
Donc : \(\large \dfrac{P_\mathrm{utile}}{Q_\mathrm{V}}=\rho\times g\times\left(Z_2-Z_1\right)\)
\(\large P_\mathrm{utile}=Q_\mathrm{V}\times\rho\times g\times\left(Z_2-Z_1\right)\)
\(\large P_\mathrm{utile}=7,07\cdot{10}^{-3}\times1000\times9,8\times\left(26-\left(-5\right)\right)\)
\(\large\color{blue} P_\mathrm{utile}=2,15 \cdot 10^3\ \mathrm{W}\)
Question⚓
Q22. (RÉA) En déduire la puissance absorbée \(\large P_\text{absorbée}\) par la pompe sachant que son rendement est de \(\large 80 \%\).
Réponse : \(P_\text{absorbée}=2,69\ \mathrm{kW}\)
👨🎓 Équation de Bernoulli généralisée (pour un fluide réel)⚓
Complément : [Document n°4] - Équation de Bernoulli généralisée
Dans un fluide réel, il existe des frottements, entre le fluide et les parois de la conduite, mais aussi entre les particules de fluide. Un fluide possède donc une viscosité[*].
Ces frottements entraînent alors une perte naturelle de pression du fluide. La pression diminue même de manière linéaire : c'est-à-dire proportionnelle à la longueur de la canalisation. \(\large P_\mathrm{B}\) est plus petit que ce qu'il devrait être. La pression diminue également avec les accidents de parcours.
On note \(\large \Delta P\) ces pertes de pression : \(\large \Delta P>0\)
Ce phénomène de diminution de la pression s'appelle « les pertes de charge ».
On a donc :
Rappels (voir Doc.5, 6, 7 et 8 de l'Activité n°5) :
\(\large \Delta P_\text{tot}=\Delta P_\text{rég} + \Delta P_\text{sing}\) avec : \(\large \Delta P_\text{rég}=\lambda \times\dfrac{\rho \times\ell\times \mathrm{v}^2}{2\times D}\)
Complément : [Document n°5] - Les travaux de Reynolds
Pour résoudre le problème d'écoulement des fluides réels, on fait appel à des résultats expérimentaux, ceux de Reynolds (1883).
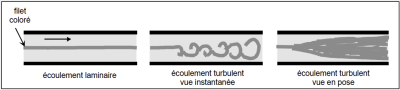
Les expériences réalisées par Reynolds en 1883 sur l'écoulement d'un fluide dans une conduite cylindrique rectiligne ont montré l'existence de deux régimes d'écoulement : laminaire et turbulent.
En utilisant des fluides divers (de viscosités différentes), et en faisant varier le débit et le diamètre de la canalisation, Reynolds a montré que l'on pouvait déterminer le régime d'écoulement (laminaire ou turbulent) via l'estimation d'un nombre sans dimension, appelé nombre de Reynolds et noté \({Re}\), calculable à l'aide de la relation :
Avec :
\(\large \rho\) : masse volumique en \(\large \mathrm{kg.m^{-3}}\)
\(\large \mathrm{v}\) : vitesse en \(\large \mathrm{m.s^{-1}}\)
\(\large D\) : diamètre de la canalisation en \(\large \mathrm{m}\)
\(\large \eta\) : viscosité dynamique[*] du fluide.
Dans le système international (SI), l'unité de viscosité dynamique est le Poiseuille noté Pa.s : \(\large 1 \ \mathrm{Pa.s} = 1\ \mathrm{kg.s^{-1}}\)
Le nombre de Reynolds peut aussi se calculer à l'aide de la relation :
Avec :
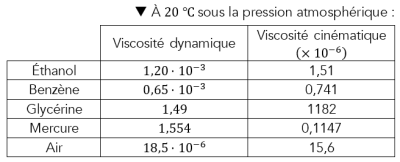
\(\large \nu\) : viscosité cinématique[*] du fluide.
Il vient alors : \(\large \nu=\dfrac{\eta}{\rho}\)
La viscosité cinématique et la viscosité dynamique sont deux grandeurs liées qui permettent de quantifier la viscosité (les frottements d'un fluide).
Bien que la transition d'un régime d'écoulement à un autre se fasse progressivement, on considère généralement que l'écoulement est laminaire pour \(\large Re<2000\), et que l'écoulement est turbulent pour \(\large Re>3000\). (Il faudra toujours tenir compte des consignes de l'énoncé).
Dans le cas d'un écoulement laminaire, il existe une relation entre le coefficient de pertes de charges linéaire \(\large \lambda\) et le nombre de Reynolds \(\large Re\) : \[\fbox{$ {\large { \text{ } \lambda =\dfrac{ 64 }{ Re } \text{ } } } $}\]
💪 Appliquer la loi de conservation pour un fluide réel
Faire les exercices suivants.
🏋️♂️ Exercice n°6 : Fluide réel et nombre de Reynolds⚓
Déterminer le régime d'écoulement dans une conduite de \(\large 3\ \mathrm{m}\) de diamètre pour :
Question⚓
Q23. (RÉA) De l'eau circulant à la vitesse \(\mathrm{v}=10,5\ \mathrm{m.s^{-1}}\) et de viscosité cinématique \(\large 1 \cdot 10^{-6}\ \mathrm{m^2/s}\).
Aide : Comparer la valeur calculée aux valeurs de référence pour déterminer le régime d'écoulement
Réponse : \(Re=3,15⋅10^5\)
Question⚓
Q24. (RÉA) Du fuel lourd à 10 °C circulant à la même vitesse (viscosité cinématique \(290\cdot10^{-6}\ \mathrm{m^2/s}\)).
Aide : Idem question précédente.
Réponse : \(Re=1,086\cdot10^3\)
🏋️♂️ Exercice n°7 :⚓
Du fuel lourd de viscosité dynamique \(\large \eta=0,110\ \mathrm{Pa.s}\) et de densité \(\large d=0,932\) circule dans un tuyau de longueur \(\large L=1\ 650\ \mathrm{m}\) et de diamètre \(\large D=25,0\ \mathrm{cm}\) à un débit volumique \(\large Q_V=19,7\ \mathrm{L/s}\).
On donne la masse volumique de l'eau \(\large \rho_{eau}=1\ 000\ \mathrm{kg.m^{-3}}\).
Question⚓
Q25. (RÉA) Déterminer la viscosité cinématique \(\large nu\) du fuel en \(\large \mathrm{m^2/s}\).
Aide : Déterminer avant la masse volumique du fuel.
Réponse : \(\nu=1,18\cdot{10}^{-4}\ \mathrm{m^2/s}\)
Solution⚓
A6-Q25.
Déterminons d'abord la masse volumique du fuel :
\(\large \rho_\mathrm{fuel}=d\times\rho_\mathrm{eau}\)
\(\large \rho_\mathrm{fuel}=0,932\times1000\)
\(\large \rho_\mathrm{fuel}=932\ \mathrm{kg.m^{-3}}\)
Calculons maintenant la viscosité cinématique :
\(\large \nu=\dfrac{\eta}{\rho}\)
\(\large \nu=\dfrac{0,110}{932}\)
\(\large\color{blue} \nu=1,18\cdot{10}^{-4}\ \mathrm{m^2/s}\)
Question⚓
Q26. (RÉA) Calculer la vitesse d'écoulement \(\large \mathrm{v}\).
Réponse : \(\mathrm{v}=40,1\ \mathrm{cm/s}\).
Solution⚓
A6-Q26.
\(\large \mathrm{v}=\dfrac{Q_\mathrm{V}}{S}=\dfrac{Q_\mathrm{V}}{\ \pi\times\frac{D^2}{4}\ }\)
\(\large \mathrm{v}=\dfrac{4\ Q_\mathrm{V}}{\ \pi\times D^2\ }\)
\(\large \mathrm{v}=\dfrac{4\times19,7\cdot{10}^{-3}}{\pi\times\left(25,0\cdot{10}^{-2}\right)^2}\)
\(\color{blue} \large \mathrm{v}=0,401\ \mathrm{m/s}\)
Question⚓
Q29. (RÉA) Déterminer le coefficient\( \large{\lambda}\) de pertes de charge linéaire
Aide : Utiliser la bonne formule en fonction du régime d'écoulement
Réponse : \(\lambda=7,53\cdot{10}^{-2}\)
Question⚓
Q30. (RÉA) Calculer la perte de charge \(\large \Delta P\) dans le tuyau.
Aide : Appliquer la formule du calcul des pertes de charges.
Réponse : \(\Delta P=0,372\ \mathrm{bar}\)
Solution⚓
A6-Q30.
\(\large \Delta P=\lambda\times\dfrac{\rho\times L\times\mathrm{v}^2}{2\times D}\)
\(\large \Delta P=7,53\cdot{10}^{-2}\times\dfrac{932\times1650\times{0,401}^2}{2\times25,0\cdot{10}^{-2}}\)
\(\large \color{blue} \Delta P=3,72\cdot{10}^4\ \mathrm{Pa}\)
\(\large \Delta P=0,372\ \mathrm{bar}\)
🏋️♂️ Exercice n°8 :⚓
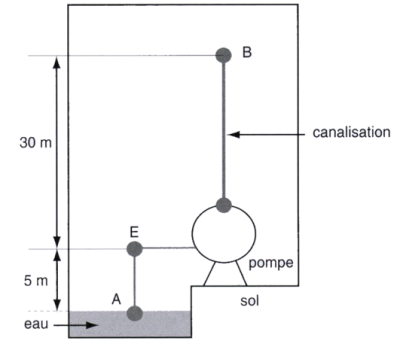
On s'intéresse au circuit d'alimentation en eau potable d'une tour maritime de \(45\ \mathrm{m}\) de hauteur. Le circuit est schématisé ci-contre.
Les pressions en A et B sont supposées égales à la pression atmosphérique.
On donne :
Masse volumique de l'eau :\(\large \rho=1\ 000\ \mathrm{kg.m^{-3}}\)
L'accélération de la pesanteur \(\large g=\ 9,81\ \mathrm{m.s^{-2}}\)
Diamètre de la canalisation : \(\large D=2,7\ \mathrm{cm}\)
Débit volumique : \(\large q_\mathrm{V}=3,5\cdot{10}^{-4}\ \mathrm{m^{3}.s^{-1}}\)
\(\large P_\mathrm{atm}=1\cdot{10}^5\ \mathrm{Pa}\)
Question⚓
Q31. (RÉA) On veut remplir un récipient de \(\large 20\ \mathrm{L}\), situé en B. Combien de temps faut-il pour le remplir ?
Aide : Utiliser la définition du débit volumique.
Réponse : \(\Delta t=57,1\ \mathrm{s}\)
Solution⚓
A6-Q31.
Question⚓
Q32. (RÉA) Calculer la vitesse d'écoulement dans la canalisation.
Aide : Utiliser la relation entre le débit et la vitesse.
Réponse : \(\mathrm{v}=0,611\ \mathrm{m.s^{-1}}\)
Question⚓
Q33. (RÉA) Calculer la pression \(\large p_\mathrm{E}\) à l'entrée de la pompe en utilisant la relation de Bernoulli, les pertes en charge entre A et E valant \(\large \Delta P_1=1\ 000\ \mathrm{Pa}\).
Aide : Utiliser l'équation de Bernoulli sans machine et avec pertes de charges.
Réponse : \(p_{\mathrm{E}}=5,00\cdot{10}^4\ \mathrm{Pa}\)
Solution⚓
A6-Q33.
On défini \(\large z_\mathrm{A}=0\) et \(\large z_\mathrm{E}=5\ \mathrm{m}\) (et aussi \(z_\mathrm{B}=35\ \mathrm{m}\) ).
On applique l'équation de Bernoulli sans machine et avec des pertes de charges entre A et E, avec \(\large \mathrm{v_A}=\mathrm{v_E}=\mathrm{v}\) et \(\large p_A=P_\mathrm{atm}\).
\(\large p_\mathrm{A}+\rho\ g\ z_\mathrm{A}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2 =\ p_\mathrm{E}+\rho\ g\ z_\mathrm{E}+\dfrac{1}{2} \ \rho \ \mathrm{v_E}^2+\Delta P_1\)
\(\large p_\mathrm{E} = P_\mathrm{atm}-\rho\ g\ z_\mathrm{E} - \Delta P_1\)
\(\large p_\mathrm{E} = 1\cdot{10}^5-1000\times9,81\times 5-1000\)
\(\large \color{blue} p_\mathrm{E} = 5,00\cdot{10}^4\ \mathrm{Pa}\)
Question⚓
Q34. (RÉA) Pour éviter les problèmes de cavitation (vaporisation du liquide dans la canalisation très dommageable pour la pompe) la pression de l'eau doit être dans le cas étudié supérieure à \(\large p=1\ 700\ \mathrm{Pa}\) à l'entrée de la pompe. Risque-t-on un problème de cavitation ?
Solution⚓
A6-Q34.
La pression en E est d'environ \(\large 50\ 000\ \mathrm{Pa}\) à \(\large 5\ \mathrm{m}\) de hauteur, il ne faudrait pas que la pompe soit beaucoup plus haute, sinon la pression pourrait devenir inférieure à la valeur de \(\large 1\ 700\ \mathrm{Pa}\), ce qui occasionnerait de la cavitation.
Question⚓
Q35. (RÉA) Les pertes en charge sur l'ensemble du circuit sont estimées à \(\large \Delta P_2=6\ 500\ \mathrm{Pa}\). Calculer la puissance hydraulique \(\large P_\mathrm{h}\) de la pompe.
Aide : Utiliser l'équation de Bernoulli avec machine et avec pertes de charges. Remplacer \(W_{12}\) par son expression.
Réponse : \(P_\mathrm{h}=122\ \mathrm{W}\)
Solution⚓
A6-Q35.
On applique l'équation de Bernoulli avec machine et avec pertes de charges entre A et B.
On a \(\large \mathrm{v_A}=\mathrm{v_B}=\mathrm{v}\) et \(\large p_A=P_\mathrm{atm}\). On défini \(\large z_\mathrm{A}=0\) et \(\large z_\mathrm{B}=35\ \mathrm{m}\).
\(\large p_\mathrm{A}+\rho\ g\ z_\mathrm{A}+\dfrac{1}{2} \ \rho \ \mathrm{v_A}^2 =\ p_\mathrm{B}+\rho\ g\ z_\mathrm{B}+\dfrac{1}{2} \ \rho \ \mathrm{v_B}^2+\Delta P\)
(... quelques étapes ne sont pas écrites ici ...)
\(\large P_\mathrm{h}=q_\mathrm{V}\times \Big( \ \rho\times g\times \left( z_\mathrm{B}-z_\mathrm{A} \right) +\Delta P \ \Big)\)
\(\large P_\mathrm{h}=3,5\cdot{10}^{-4}\times\Big(1000\times9,81\times\big(\ 35-0\ \big)+6500\Big)\)
\(\large \color{blue} P_\mathrm{h}=122\ \mathrm{W}\)