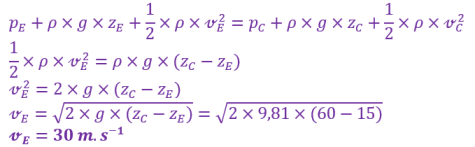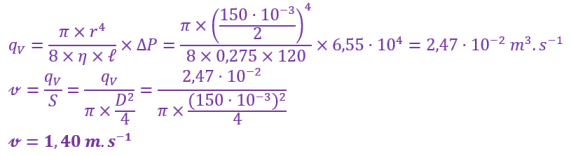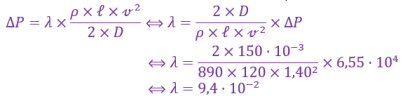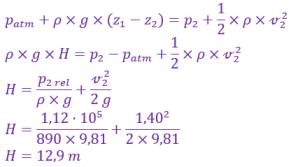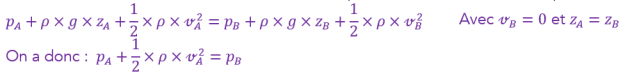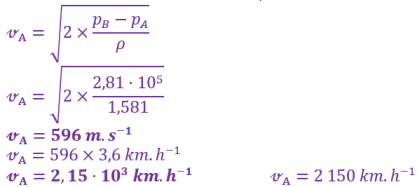Partie n°1 - Avec des fluides parfaits⚓
Exercice n°1 : Distribution d'eau à partir d'un château d'eau⚓
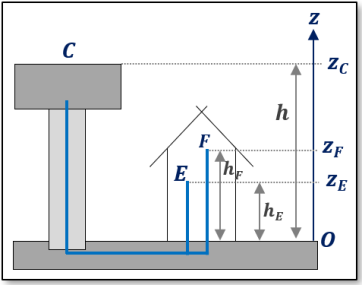
La surface libre C de l'eau contenue dans un château d'eau est à une hauteur \(\large h=60\ \mathrm{m}\) du sol.
Un immeuble est alimenté par ce château d'eau. Le sol sur lequel sont construits l'immeuble et le château d'eau est horizontal (voir figure ci-contre). Deux robinets sont présents en E et F.
Données :
masse volumique de l'eau \(\large \rho=1\ 000\ \mathrm{kg.m^{-3}}\)
\(\large g=\ 9,81\ \mathrm{m.s^{-2}}\)
pression atmosphérique normale \(\large p_0={10}^5\ \mathrm{Pa}\)
Question⚓
Q1. (RÉA) Calculer l'écart entre la pression de l'eau au niveau d'un robinet E situé à \(15\ \mathrm{m}\) de hauteur dans l'immeuble et la pression atmosphérique (on considère le robinet fermé). Justifier l'équation utilisée.
Aide : Le fluide est-il au repos ou en mouvement ? Quelle équation choisir ?
Valeur à trouver : \(4,41\cdot{10}^5\ \mathrm{Pa}\)
On ouvre uniquement le robinet E. La section S de la canalisation alimentant ce robinet est de \(\large 2,01\ \mathrm{cm^2}\) (diamètre de \(\large 16\ \mathrm{mm}\)). Cette section sera considérée comme très très inférieure à celle de la surface libre du château d'eau. En utilisant l'équation de Bernoulli entre les points C et E, répondre aux questions suivantes.
Question⚓
Q5. (ANA) Que peut-on dire de la valeur \(\large \mathrm{v_C}\) de la vitesse d'écoulement au niveau du château d'eau par rapport à celle au niveau du robinet \(\large \mathrm{v_E}\) ?
Question⚓
Q7. (RÉA) Calculer le débit volumique dans cette canalisation.
Valeur à trouver : \(Q_\mathrm{VE}=6,0\ \mathrm{L.s^{-1}}\)
On ferme le robinet E et on ouvre uniquement le robinet F situé à une hauteur de \(\large 25\ \mathrm{m}\). La section S de la canalisation alimentant ce robinet est également de \(\large 2,01\ \mathrm{cm}^2 \)(diamètre de \(\large 16\ \mathrm{mm}\)).
Question⚓
Q9. (RÉA) Calculer alors la vitesse d'écoulement dans la canalisation (au niveau du robinet F) puis le débit volumique dans cette canalisation.
Aide : Utiliser l'équation de Bernoulli entre F et C.
Valeur à trouver : \(\mathrm{v_F}=26\ \mathrm{m.s^{-1}}\) et \(\large Q_\mathrm{VF}=5,2\ \mathrm{L.s^{-1}}\)
Partie n°2 - Avec des fluides réels⚓
Exercice n°2 : Écoulement laminaire – Pertes de charge⚓
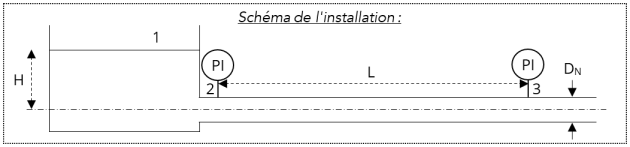
Un écoulement d'huile de graissage de viscosité dynamique moyenne \(\large \eta=0,275\ \mathrm{Pa.s}\) et de masse volumique \(\large \rho=890\ \mathrm{kg.m^{-3}}\) se fait dans un tube horizontal de diamètre nominal \(\large D_\mathrm{N}=150\ \mathrm{mm}\) et de longueur \(\large L=120\ \mathrm{m}\). On installe sur ce tube, deux capteurs de pression statique constitués par deux manomètres de Bourdon (PI pour Pressure Indicator sur le schéma) ; les valeurs des pressions relatives données par ces appareils sont : \(\large p_\mathrm{2\ rel}=1,12\ \mathrm{bar}\) et \(\large p_\mathrm{3\ rel}=0,465\ \mathrm{bar}\).
Données :
\(\large g=\ 9,81\ \mathrm{m.s^{-2}}\)
pression atmosphérique normale \(\large p_0={10}^5\ \mathrm{Pa}\)
Complément : Rappels
Loi de Poiseuille pour un écoulement laminaire dans une conduite horizontale de longueur \(\large \ell\) :
Avec :
\(\large R\) : Rayon de la canalisation cylindrique en \(\mathrm{m}\) ;
\(\large \eta\) : viscosité dynamique du fluide exprimée en \(\mathrm{Pa.s}\) ;
\(\large \ell\) : longueur de la canalisation, exprimée en \(\mathrm{m}\) ;
\(\large q_\mathrm{V}\) : vitesse moyenne du fluide, exprimée en \(\mathrm{m^3.s^{-1}}\) ;
\(\large \Delta P\) : pertes de charges linéraires.
Les pertes de charges linéaires se calculent à l'aide de la relation :
Avec :
\(\large \lambda\) : coefficient de pertes de charges linéaire sans unité (noté également \(\large f\) dans la fiche annexe), il dépend du régime d'écoulement, donc du nombre de Reynolds \(\large Re\)
\(\large \rho\) : masse volumique du fluide, exprimée en \(\mathrm{kg.m^{-3}}\)
\(\large \mathrm{v}\) : vitesse moyenne du fluide, exprimée en \(\mathrm{m.s^{-1}}\)
\(\large \ell\) : longueur de la canalisation, exprimée en \(\mathrm{m}\)
\(\large D\) : diamètre de la canalisation, exprimée en \(\mathrm{m}\)
Question⚓
Q10. (RÉA) Calculer en \(\large \mathrm{Pa}\) la différence de pression \(\large \Delta p_{23}=p_2-p_3\).
Valeur à trouver : \(\Delta p_{23}=6,55\cdot{10}^4\ \mathrm{Pa}\)
Question⚓
Q12. (RÉA) En déduire la valeur du nombre de Reynolds \(\large Re\) (voir feuille annexe de l'activité n°4). Montrer qu'il s'agit bien d'écoulement laminaire.
Valeur à trouver : \(Re=680\)
Question⚓
Q15. (RÉA) Donner la valeur numérique du produit \(\large \lambda\times Re\). Conclure.
Question⚓
Q16. (RÉA) Donner la relation de Bernoulli entre les points 1 et 2 (sans faire de calcul) en négligeant tout frottement entre ces deux points (notamment la perte de charge singulière point A). Quelles sont les conditions d'application ?
Solution⚓
A7-Q16. (exo-2)
\(\large p_1+\rho\times g\times z_1+\frac{1}{2}\times\rho\times\mathrm{v}_1^2\ =\ p_2+\rho\times g\times z_2+\frac{1}{2}\times\rho\times\mathrm{v}_2^2\)
Comme la surface libre du réservoir est très grande par rapport à la section de la canalisation, on peut dire que \(\mathrm{v}_1\approx0\ \mathrm{m.s^{-1}}\). De plus on peut écrire : \(Z_1-z_2=H\). Et enfin, \(p_1=p_\mathrm{atm}\).
Question⚓
Q17. (RÉA) Appliquer la relation de Bernoulli entre les points 1 et 2 pour en déduire l'expression littérale donnant \(\large H\) en fonction de \(\large p_\mathrm{atm}\) , \(\large p_\mathrm{2\ rel}\), \(\large \mathrm{v}\), \(\large \rho\) et \(\large g\). Calculer numériquement \(\large H\).
Valeur à trouver : \(H=12,9\ \mathrm{m}\)
Exercice n°3 : Équation de continuité et théorème de Bernoulli dans une lance à incendie⚓
Pour une petite lance à incendie à eau, le diamètre d'entrée est \(\large 40\ \mathrm{mm}\), celui de sortie vaut \(\large 14\ \mathrm{mm}\). Le débit est de \(\large 250\ \mathrm{L/min}\).
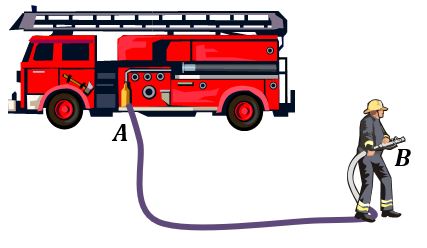
On considère que l'entrée et la sortie d'eau sont à des hauteurs identiques, la longueur de la lance étant de \(\large 30\ \mathrm{m}\).
Question⚓
Q21. (RÉA) Si la lance est orientée verticalement, à quelle hauteur arriverait le jet d'eau si l'on néglige tous les frottements.
Aide : Utiliser l'équation de Bernoulli entre B et C, l'eau s'écoule dans l'air, donc \(p_\mathrm{B}=...\).
Valeur à trouver : \(h=37,4\ \mathrm{m}\)
Solution⚓
A7-Q21. (exo-3)
On cherche l'altitude atteinte par l'eau \(\large z_\mathrm{C}\) telle que \(\large z_\mathrm{C}-z_\mathrm{A}=h\). L'eau s'écoule toujours dans l'air, donc \(\large p_\mathrm{B}=p_0=p_\mathrm{C}\). L'eau en \(\large z_\mathrm{C}\) aura une vitesse nulle : \(\large \mathrm{v_C}=0\ \mathrm{m.s^{-1}}\). Il n'y a aucun frottement donc aucunes pertes de charge.

La perte de charge dans les tuyaux est de \(\large 1,5\ \mathrm{bar}\) pour \(\large 100\ \mathrm{m}\) (application du théorème de Bernoulli).
Question⚓
Q22. (RÉA) Calculer la nouvelle pression \(\large p^\prime\) que doit fournir le compresseur du camion pour compenser la perte de charge.
Aide : Calculer les pertes de charges sur la longueur. Puis utiliser l'équation de Bernoulli entre A et B avec pertes de charge, l'eau s'écoulant encore dans l'air
Valeur à trouver : \(p^\prime=5,10\ \mathrm{bar}\)
Solution⚓
A7-Q22. (exo-3)
Les pertes de charges dans le tuyau sont de \(1,5\ \mathrm{bar}\) pour \(100\ \mathrm{m}\) et le tuyau a une longueur de \(30\ \mathrm{m}\) donc :
\(\large \Delta P=\dfrac{30}{100}\times1,5\ \mathrm{bar}=0,45\ \mathrm{bar}=4,5\cdot{10}^4\ \mathrm{Pa}\)
On peut écrire la relation de Bernoulli entre A et B afin qu'on ait les mêmes conditions en B que pour la question précédente. On a donc encore \(\large z_\mathrm{A}=z_\mathrm{B}\) et en B l'eau s'écoule dans l'air, donc \(\large p_\mathrm{B}=p_0={10}^5\ \mathrm{Pa}\).
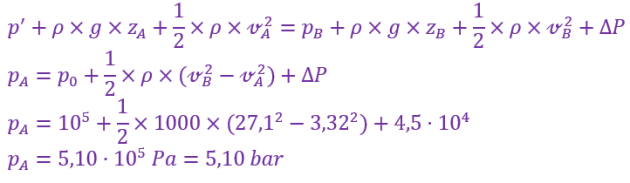
Exercice n°4 : Le tube de Pitot⚓
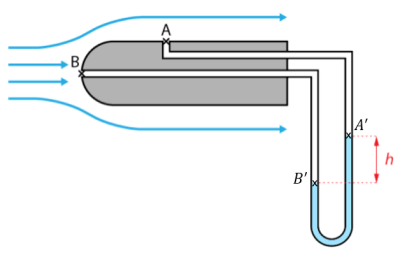
Le tube de Pitot est un système de mesure de la vitesse d'un fluide, principalement dans le cas de l'air en aviation. Le principe est de mesurer la différence de pression entre deux prises de pressions :
Une prise de pression statique dont l'axe est perpendiculaire à l'écoulement du fluide (point \(\large A\) sur le schéma). La vitesse du fluide est mesurée en ce point.
Une prise de pression dynamique dont l'axe est parallèle à l'écoulement du fluide (point \(\large B\) sur le schéma). La vitesse du fluide en ce point est nulle car le fluide est stoppé par le tube de Pitot.
Le fluide en déplacement sera considéré comme étant de l'air dans cet exercice.
La pression au point \(\large A\) se retrouve au point \(\large A^\prime\) car la différence de hauteur entre \(\large A\) et \(\large A^\prime\) est négligeable pour le fluide en déplacement étudié (de l'air). Même chose entre \(\large B\) et \(\large B^\prime\).
Question⚓
Q23. (ANA/RÉA) Si l'on fait l'hypothèse de l'absence de pertes de charge entre les points A et B, et que les points A et B sont à la même hauteur \(\large \left(\ z_\mathrm{A}=z_\mathrm{B}\ \right)\), écrire l'équation de Bernoulli entre les points A et B.
Aide : Penser aux simplifications → que valent les vitesses ? Que valent les altitudes \(z\) ?
Question⚓
Q25. (RÉA)) Si on considère un manomètre à tube en U, contenant un fluide de masse volumique \(\large \rho_0\), exprimer la différence de pression \(\large p_{\mathrm{B}^\prime}-p_{\mathrm{A}^\prime}\) en fonction de la dénivellation \(\large h\).
Aide : Le fluide à l'intérieur du tube en U est-il en mouvement ? Quelle relation peut-on employer dans ce cas ?
Solution⚓
A7-Q25. (exo-4)
Comme le fluide de masse volumique \(\large \rho_0\) est immobile, on applique le principe fondamental de l'hydrostatique entre \(\large A^\prime\) et \(\large B^\prime\) : \(\large p_\mathrm{A^\prime}+\rho_0\cdot g\cdot z_\mathrm{A^\prime}=p_\mathrm{B^\prime}+\rho_0\cdot g\cdot z_\mathrm{B^\prime}\)
\(\large p_\mathrm{B^\prime}-p_\mathrm{A^\prime}=\rho_0\cdot g\cdot\left(z_\mathrm{A^\prime}-z_\mathrm{B^\prime}\right)\)
Si on définit un axe des altitudes orienté vers le haut, alors \(\large z_\mathrm{A^\prime}-z_\mathrm{B^\prime}=h\), on a donc : \(\large \color{blue} p_\mathrm{B^\prime}-p_\mathrm{A^\prime}=\rho_0\cdot g\cdot h\)
Question⚓
Q26. (RÉA) En déduire la différence de pression \(\large p_\mathrm{B}-p_\mathrm{A}\) en fonction de la dénivellation \(\large h\).
Solution⚓
A7-Q26. (exo-4)
Comme \(\large p_\mathrm{B}=p_\mathrm{B^\prime}\) et \(\large p_\mathrm{A}=p_\mathrm{A^\prime}\), alors on a \(\large p_\mathrm{B}-p_\mathrm{A}=p_\mathrm{B^\prime}-p_\mathrm{A^\prime}=\rho_0\cdot g\cdot h\). Donc : \(\large \color{blue} p_\mathrm{B}-p_\mathrm{A}=\rho_0\cdot g\cdot h\).
Question⚓
Q27. (RÉA) En déduire l'expression de la vitesse en fonction de la dénivellation \(\large h\).
Aide : : Il faut combiner la réponse précédente à celle de la question Q24.
Un Airbus A350 vole à la vitesse de \(\large 905\ \mathrm{km/h}\). À l'altitude de croisière (environ \(\large 13\ 000\ \mathrm{m}\)), la masse volumique de l'air est \(\large \rho_{air}=1,581\ \mathrm{kg.m^{-3}}\).
Question⚓
Q28. (RÉA) Quelle sera la différence de pression mesurée par le manomètre en U du tube de Pitot ?
Valeur à trouver : \(5,00\cdot{10}^4\ \mathrm{Pa}\)
Question⚓
Q29. (RÉA) Que vaut la dénivellation \(\large h\) si le fluide du tube en U est de l'eau ? Conclure quant au fluide devant se trouver dans le manomètre.
Valeur à trouver : \(h=5,10\ \mathrm{m}\)
Solution⚓
A7-Q29. (exo-4)
\(\large p_\mathrm{B}-p_\mathrm{A}=\rho_0\cdot g\cdot h\ \ \ \ \ \ \Rightarrow\ \ h=\dfrac{p_\mathrm{B}-p_\mathrm{A}}{\rho_0\cdot g}\)
\(\large h=\dfrac{5,00\cdot{10}^4}{1\ 000\times9,81}\)
\(\large \color{blue} h=5,10\ \mathrm{m}\)
La dénivellation est très grande pour être mesurée ainsi dans un avion. Le fluide qui doit se trouver dans le manomètre doit avoir une masse volumique bien plus grande.
Question⚓
Q30. (RÉA) Que vaut la dénivellation \(\large h\) si le fluide du tube en U était du mercure ? Conclure quant au manomètre en U.
On donne : \(\rho_\mathrm{Hg}=13\ 500\ \mathrm{kg/m^3}\)
Valeur à trouver : \(h=37,8\ \mathrm{cm}\)
Solution⚓
A7-Q30. (exo-4)
\(\large h=\dfrac{p_\mathrm{B}-p_\mathrm{A}}{\rho_0\cdot g}=\dfrac{5,00\cdot{10}^4}{13\ 500\times9,81}\)
\(\large \color{blue} h=0,378\ \mathrm{m}=37,8\ \mathrm{cm}\)
Même avec un fluide de masse volumique très importante, la dénivellation est encore trop importante pour être mesurée ainsi dans un avion. Il faut un autre type de manomètre, par exemple un manomètre à tube de bourdon.
Complément : Note
Dans un avion on utilise plutôt des capteurs de pression électronique.
Le Concorde volait à une altitude d'environ \(\large 17\ 000\ \mathrm{m}\) où la masse volumique de l'air est aussi \(\large \rho_{air}=1,581\ \mathrm{kg.m^{-3}}\). La différence de pression mesurée par un capteur de pression indiquerait une valeur de \(\large 2,81\ \mathrm{bar}\).