Activité n°4 : Exercices d'application - [Chapitre : Échanges thermiques - Calorimétrie]

Titre de l'activité : Activité n°4 : Exercices d'application - [Chapitre : Échanges thermiques - Calorimétrie]

Durée : 1h - 1h30min

Compétences

ANA - Exploiter ses connaissances, les informations extraites ou les résultats obtenus
ANA - Élaborer une démarche
APP - Rechercher et extraire l'information
APP - Connaître le vocabulaire, les symboles et les unités mise en œuvre
APP - Mobiliser les connaissances en rapport avec le problème
RÉA - Calculer, utiliser une formule
RCO - Restituer des connaissances

Notions

Associer un changement d’état macroscopique à l’évolution des interactions entre les entités à l’échelle microscopique.
Échanges thermiques ; conservation, transferts et transmission d’énergie
Appliquer la conservation de l’énergie à l’étude des transferts thermiques d’un système avec le milieu extérieur avec et sans changement d’état.
Établir par la mesure un classement des capacités thermiques de différents matériaux.

Rappel : Données pour tous les exercices

Capacité thermique massique de l'eau liquide : \(c_{\text{eau}} = 4\,180 \; \mathrm{J.kg^{-1}.K^{-1}}\)

💪 Exercice n°1 : La bouilloire ⚓

À l'aide d'une résistance chauffante, l'énergie électrique est convertie et fournie une quantité de chaleur. La capacité thermique de l'eau permet de connaître le temps de chauffage (la capacité thermique de la bouilloire est supposée négligeable) : pour un litre d'eau ( 1 L ) avec une bouilloire de 2,00 kW il faut une durée de 2 min 47 s pour faire monter la température de 20,0°C à 100°C.

Question⚓

Q1. Retrouver ce résultat (la durée) par une démarche calculatoire.

Donnée supplémentaire : \(\rho_{eau}=1\, 000\: g.L^{-1}\)

Solution ⚓

Act.n°4 - Ex.1

Q1.

On a : \(\theta_i=20\ \mathrm{^\circ C^{-1}}\) et \(\theta_f=100\ \mathrm{^\circ C}\) et \(P=2\ kW\).

\(m_{eau}=\rho_{eau}\times V_{eau} \text{ avec } V_{eau}=1\ L\)

Comme \(c_{eau}\) est en \(\mathrm{J.kg^{-1}.^\circ C^{-1}}\), on va convertir la masse volumique : \(\rho_{eau}=1,000\ kg.L^{-1}\).

D'après ce qui a été vu précédemment, on a : \(\Delta U=Q=m\cdot c\cdot\Delta\theta\).

Mais comme on a aussi \(Q=P\times\Delta t\), on a alors :

\[\begin{array}{rll} \large { Q_{\text{eau}} = m\times c_{\text{eau}} \times \Delta \theta =P\times\Delta t } & \Longleftrightarrow & \large { \Delta t=\dfrac{\rho_{eau}\times V_{eau}\times c_{eau}\times\Delta\theta}{P} } \\ & \Longleftrightarrow & \large { \Delta t=\dfrac{1,000\times1,00\times4\ 180\times\left(100-20,0\right)}{2,00\cdot{10}^3} } \\ & \Longleftrightarrow & \large {{\color{blue} \Delta t=167\ s }} \\ \\ & \Longleftrightarrow & \large {{\color{red} \Delta t=2\ min \ 47 \ s }} \end{array}\]

💪 Exercice n°2 : Détermination de la capacité thermique massique de l'huile ⚓

On veut déterminer la capacité thermique massique de l'huile contenue dans un radiateur à bain d'huile.

On verse 0,5 L d'huile dans un récipient calorifugé. On plonge un thermoplongeur relié à un joulmètre et on relève la température. Celle-ci s'élève de 8°C pour une énergie fournie de 8,1 kJ.

Donnée : masse volumique de l'huile : \(\rho_{huile}=0,800\: kg.L^{-1}\).

Question⚓

Q2. Quelle est, en kg, la masse de 0,5 L d'huile ?

Solution ⚓

Act.4 - Ex.2

Q2.

\(m_{huile}=\rho\times V_{huile}=0,800\times0,5=0,400\: kg \; \;\;\; \left(=400\ g\right)\)

Question⚓

Q3. Écrire la relation entre l'énergie thermique Q fournie à l'huile, la masse d'huile, la capacité thermique et la variation de température ?

Solution ⚓

Act.4 - Ex.2

Q3. \(Q=m_{huile}\times c_{huile}\times\Delta\theta \text{ avec } \Delta\theta=+8\ ^\circ \text{C}\)

Question⚓

Q4. Calculer la capacité thermique massique \(c_{huile}\) de l'huile.

Solution ⚓

Act.4 - Ex.2

Q4.

\[\begin{array}{rll} \large { c_{huile} } & = & {\large { \dfrac { Q } { m_{huile} \times \Delta \theta } } } \\ & = & {\large { \dfrac {8,1 \cdot {10}^3 } { 0,400 \times 8 } } } \\ & = & {\large {{\color{blue} 2,5\cdot{10}^3\ \mathrm{J.kg^{-1}.^\circ C^{-1}} }} } \\ & = & {\large {{\color{blue} 2,5\ \mathrm{kJ.kg^{-1}.^\circ C^{-1}} }} } \end{array}\]

💪 Exercice n°3 : Mur à accumulation d'énergie ⚓

La température d'un mur de briques pleines exposé au soleil passe de 14°C à 35°C.

Donnée : \(c_{brique}=840\: \mathrm{kJ.kg^{-1}.^\circ C^{-1}}\).

Question⚓

Q5. Sous quelle forme le mur emmagasine-t-il de l'énergie ?

Solution ⚓

Act.4 - Ex.3

Q5. Le mur emmagasine l'énergie sous forme thermique (de chaleur) : sa température augmente.

Question⚓

Q6. La masse du mur étant de 800 kg, calculer sa variation d'énergie interne en considérant que le mur ne fait que recevoir de l'énergie du Soleil.

Solution ⚓

Act.4 - Ex.3

Q6.

\(\Delta U=W+Q\)

Le mur ne fait que recevoir de l'énergie du Soleil. Donc il ne reçoit que de l'énergie thermique :

\(Q=m_{brique}\times c_{brique}\times\left(\theta_f-\theta_i\right)\)

Donc son énergie internet augmente telle que : \(\Delta U=Q=m_{brique}\times c_{brique}\times\left(\theta_f-\theta_i\right)\)

\(\Delta U=800\times840\cdot {10}^3\times\left(35-14\right)=1,4\cdot{10}^{10}\ J\ \ \ \ \ \left(\ \ =14\ GJ\ \right)\)

La nuit la température du mur passe de 35°C à 16°C en 12 heures

Question⚓

Q7. Calculer l'énergie cédée par le mur.

Solution ⚓

Act.4 - Ex.3

Q7. L'énergie cédée par le mur est :

\(Q_{\text{cédée}}=m_{brique}\times c_{brique}\times\left(\theta_f-\theta_i\right)=800\times840\times\left(16-35\right)=-1,3\cdot{10}^7\ J\)

Question⚓

Q8. Calculer la puissance moyenne transférée.

Solution ⚓

Act.4 - Ex.3

Q8. La puissance moyenne transférée vaut :

\(P=\dfrac{\left|\text{Énergie cédée}\right|}{\Delta t}=\dfrac{\left|Q_{\text{cédée}}\right|}{\Delta t}=\dfrac{1,3\cdot{10}^7}{12\times3600}=3,0\cdot{10}^2\ W\)

Question⚓

Q9. Sous quelles formes a lieu ce transfert d'énergie thermique ?

Solution ⚓

Act.4 - Ex.3

Q9. Ce transfert d'énergie se fait principalement par rayonnement.

💪 Exercice n°4 : Utilisation d'un calorimètre pour mesurer une capacité thermique ⚓

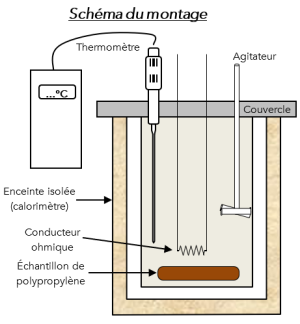
On se propose de mesurer la capacité thermique massique d'un polypropylène (PP). L'appareil de mesure utilisé est un calorimètre qui fonctionne à pression constante. Le système est parfaitement isolé.

Le conducteur ohmique placé dans le calorimètre est un fil métallique de résistance \(R=2,0\ \Omega\). Il dissipe toute l'énergie électrique qu'il reçoit sous forme d'énergie thermique grâce à l'effet Joule telle que la puissance dissipée par effet Joule vaut : \(P_{joule}=R\times I^2\).

Question⚓

Q10. Quelle est la quantité d'énergie \(W_{e\ell}\) apportée par le conducteur ohmique dans le calorimètre s'il est parcouru par un courant d'intensité \(I=2,8\ A\) pendant une durée \(\Delta t=90\ s\).

Solution ⚓

Act.4 - Ex.4

Q10.

\(W_{el}=P_{joule}\times\Delta t=R\times I^2\times\Delta t=2,0\times{2,8}^2\times90=1,4\cdot{10}^3\ J\)

On place \(m=50,0\ g\) de polypropylène dans le calorimètre à une température initiale \(\theta_0=15,0\ \mathrm{^\circ C}\).

Après un apport d'énergie \(Q=1,4\ kJ\), la température à l'intérieur du calorimètre se stabilise à \(\theta_e=28,0\ \mathrm{^\circ C}\).

Question⚓

Q11. Calculer \(Q_1\), quantité de chaleur absorbée par le calorimètre et ses accessoires, si la capacité thermique^[*] du calorimètre et de ses accessoires est \(C=18\ J.K^{-1}\).

Solution ⚓

Act.4 - Ex.4

Q11.

\(Q_1=C\times\left(\theta_e-\theta_0\right)=18\times\left(28,0-15,0\right)=2,3\cdot{10}^2\ J\)

Question⚓

Q12. Établir une relation entre \(Q\), \(Q_1\) et \(Q_2\) (quantité de chaleur absorbée par l'échantillon).

Solution ⚓

Act.4 - Ex.4

Q12.

Comme on est dans un calorimètre qui est isolé, toute l'énergie thermique fournie \(Q\) par le conducteur ohmique est intégralement transmise au calorimètre et ses accessoires et à l'échantillon de PP.

On a donc : \(Q=Q_1+Q_2\)

Question⚓

Q13. Calculer la capacité thermique massique \(C_p\) de ce polypropylène.

Solution ⚓

Act.4 - Ex.4

Q13. On a \(Q_2=c_p\times m\times\left(\theta_e-\theta_0\right)\), donc :

\[\begin{array}{rll} \large { Q=Q_1+Q_2 } & \Longleftrightarrow & {\large { Q-Q_1=c_p\times m\times\left(\theta_e-\theta_0\right) } } \\ & \Longleftrightarrow & {\large { c_p=\dfrac{Q-Q_1}{m\times\left(\theta_e-\theta_0\right)} } } \\ & \Longleftrightarrow & {\large { c_p=\dfrac{1,4\cdot{10}^3-2,3\cdot{10}^2}{50,0\cdot{10}^{-3}\times\left(28,0-15,0\right)} } } \\ & \Longleftrightarrow & {\large {{\color{blue} c_p=1,8 \cdot{10}^3\ \mathrm{J.kg^{-1}.^\circ C^{-1}} }} } \end{array}\]

Question⚓

Q14. On fournit la même quantité de chaleur à deux échantillons de masses identiques, l'un en polypropylène et l'autre en acier : déterminer qualitativement l'échantillon dont la température s'élève le plus.

Donnée : Capacité thermique massique de l'acier : \(c_{acier}=0,45\ \mathrm{J.kg^{-1}.}\mathrm{^\circ C^{-1}}\).

Solution ⚓

Act.4 - Ex.4

Q14. Pour élever d'un degré Celsius une masse de 1 kg de PP, il faut fournir une énergie de 1,8 kJ, alors qu'il faut fournir une énergie de 0,45 kJ pour élever d'un degré Celsius une masse de 1 kg d'acier.

L'élévation de température s'exprime ainsi : \(\Delta\theta=\dfrac{Q}{m\times c}\)

Ainsi, si on fournit la même énergie à la même masse de matière, l'élévation de température sera la plus grande pour l'échantillon qui a la plus petite capacité thermique massique.

Donc entre l'acier et le polypropylène, c'est l'acier dont la température s'élèvera le plus.

(Pour s'en convaincre, vous pouvez calculer \(\Delta\theta\) pour \(m=1\ kg\) et \(Q=1\ kJ\)).

💪 Exercice n°5 : Calorimètre ⚓

Définition : Valeur en eau du calorimètre (À SAVOIR)

Dans cet exercice, en plus de chercher la capacité thermique du calorimètre, nous allons chercher également quelle masse d'eau est équivalente au calorimètre et ses accessoires, en considérant donc que le calorimètre et ses accessoires se comportent comme de l'eau : c'est ce qu'on appelle la valeur en eau^[*] \(\mathbf{\mu}\) du calorimètre et de ses accessoires.

Un calorimètre contient 1 000 g d'eau à 15°C. On y verse 1 000 g d'eau à 65,5°C. La température du mélange étant à l'équilibre de 40°C.

Question⚓

Q15. Calculer la capacité thermique ainsi que la valeur en eau^[*] \(\mathbf{\mu}\) du calorimètre.

Solution ⚓

Act.4 - Ex.5

Q15.

Le système étudié est {Calorimètre et accessoires + eau froide + eau chaude}.

Le calorimètre et ses accessoires et l'eau froide sont à la température \(\theta_1=15\ \mathrm{^\circ C}\). L'eau chaude est à \(\theta_2=65,5\ \mathrm{^\circ C}\).

Le calorimètre reçoit de l'énergie et passe de \(\theta_1=15\ \mathrm{^\circ C}\) à \(\theta_f=40\ \mathrm{^\circ C}\) :
\(Q_1=C_{calo}\times\left(\theta_f-\theta_1\right)\)
L'eau froide de masse \(m_{froid}=1,000\ kg\) reçoit de l'énergie et passe de \(\theta_1=15\ \mathrm{^\circ C}\) à \(\theta_f=40\ \mathrm{^\circ C}\) :
\(Q_2=m_{froid}\times c\times\left(\theta_f-\theta_1\right)\)
L'eau chaude de masse \(m_{chaud}=1,000\ kg\) reçoit de l'énergie et passe de \(\theta_2=65,5\ \mathrm{^\circ C}\) à \(\theta_f=40\ \mathrm{^\circ C}\) :
\(Q_3=m_{chaud}\times c\times\left(\theta_f-\theta_2\right)\)

On considère le calorimètre comme isolé (=adabatique), donc on a : \(\Delta U=Q_1+Q_2+Q_3=0\)

Donc : \({\large { C_{calo}\times\left(\theta_f-\theta_1\right)+m_{froid}\times c\times\left(\theta_f-\theta_1\right)+m_{chaud}\times c\times\left(\theta_f-\theta_2\right)=0 }}\)

\[\begin{array}{rll} {\large { C_{calo}\times\left(\theta_f-\theta_1\right) } } & = & {\large { -m_{froid}\times c\times\left(\theta_f-\theta_1\right)-m_{chaud}\times c\times\left(\theta_f-\theta_2\right) } } \\ {\large { C_{calo} } } & = & {\large { \dfrac{-m_{froid}\times c\times\left(\theta_f-\theta_1\right)-m_{chaud}\times c\times\left(\theta_f-\theta_2\right)}{\theta_f-\theta_1} } } \\ {\large { C_{calo} } } & = & {\large { \dfrac{-1\ 000\cdot{10}^{-3}\times4\ 180\times\left(40-15\right)-1\ 000\cdot{10}^{-3}\times4\ 180\times\left(40-65,5\right)}{40-15} } } \\ {\large {{\color{blue} C_{calo} }} } & = & {\large {{\color{blue} 84\ \mathrm{J.^\circ C^{-1}} }} } \end{array}\]

Pour déterminer la masse en eau du calorimètre, on a : \({\large {\color{red} C_{calo}=\mu\times c}}\) donc :

\[\begin{array}{rll} {\large { \mu } } & = & {\large { \dfrac{C_{calo}}{c} } } \\ {\large { \mu } } & = & {\large { \dfrac {84} {4\ 180} } } \\ {\large {{\color{blue} \mu }} } & = & {\large {\color{blue} 2,0 \cdot 10^{-2} \ \mathrm{kg} } } \\ {\large {{\color{blue} \mu }} } & = & {\large {\color{blue} 20 \ \mathrm{g} } } \end{array}\]

💪 Exercice n°6 : Encore un autre calorimètre ⚓

Le vase calorimétrique d'un calorimètre est en aluminium, sa masse est \(m=50,0\ g\). On supposera ce calorimètre comme isolé (=adiabatique^[*]).

Question⚓

Q16. Calculer la capacité thermique de ce vase sachant que la capacité thermique massique de l'aluminium vaut \(920\ \mathrm{J.kg^{-1}.K^{-1}}\).

Solution ⚓

Act.4 - Ex.6

Q16. \(\large {C_{vase}=m\times c_{alu}=50,0\cdot{10}^{-3}\times920{\color{blue}=46,0\ J.K^{-1}}}\)

Le calorimètre contient une masse d'eau de \(100\ g \; \; \left ( c_{eau} = 4,18 \cdot 10^3\ \mathrm{J.kg^{-1}.K^{-1}} \right )\), le thermomètre et les accessoires du calorimètre ont une capacité thermique de \(15,0\ \mathrm{J.K^{-1}}\).

Question⚓

Q17. Calculer la capacité thermique totale \(C\) du calorimètre et des 100 g d'eau.

Solution ⚓

Act.4 - Ex.6

Q17.

\[\begin{array}{rll} {\large { C } } & = & {\large { C_{vase}+m_{eau}\times c_{eau}+C_{acc} } } \\ {\large { C } } & = & {\large { 46,0+100\cdot{10}^{-3}\times{4,18\cdot10}^3+15,0 } } \\ {\large {{\color{blue} C }} } & = & {\large {\color{blue} 479\ \mathrm{J.K^{-1}} } } \end{array} \]

La température initiale du calorimètre contenant les 100 g d'eau est \(T_1=17,2\ \mathrm{^\circ C}\). On introduit dans le calorimètre une certaine quantité d'eau \(m^\prime\) à la température \(T_2=100\ \mathrm{^\circ C}\), la température d'équilibre s'établit à \(T_e=38,5\ \mathrm{^\circ C}\).

Question⚓

Q18. Calculer la capacité thermique \(C^\prime\) de l'eau introduite. En déduire la valeur de la masse d'eau introduite.

Aide : Définir le système et les sous-systèmes, puis raisonner en partant de l'énergie que reçoit le sous-système {calorimètre et l'eau de départ}.

Solution ⚓

Act.4 - Ex.6

Q18.

Le système étudié est {Calorimètre avec l'eau de départ + eau chaude}.

Le calorimètre et l'eau de départ reçoivent une énergie \(Q_1\) par transfert thermique et passe de \(T_1=17,1\ \mathrm{^\circ C}\) à \(T_e=38,5\ \mathrm{^\circ C}\) :
\(Q_1=C\times\left(T_e-T_1\right)=480\times\left(38,5-17,2\right)=10,2\cdot{10}^3\ J\)
L'eau chaude cède une énergie \(Q_2\) par transfert thermique et passe de \(T_2=100\ \mathrm{^\circ C}\) à \(T_e=38,5\ \mathrm{^\circ C}\) :
\(Q_2=C^\prime\times\left(T_e-T_2\right)\)

On suppose le calorimètre comme isolé (= adiabatique), donc sa variation d'énergie interne est nulle : \(\Delta U=0=Q_1+Q_2\)

Donc :

\[\begin{array}{rll} {\large { C \times\left(T_e-T_1\right)+C^\prime\times\left(T_e-T_2\right)=0\ } } & \Longleftrightarrow & {\large { C^\prime=-\dfrac{C\times\left(T_e-T_1\right)}{T_e-T_2} } } \\ & \Longleftrightarrow & {\large { C^\prime=-\dfrac{479\times\left(38,5-17,1\right)}{38,5-100} } } \\ & \Longleftrightarrow & {\large {\color{blue} C^\prime= 167\ \mathrm{J.K^{-1}} } } \end{array} \]

Or comme \({\large {C^\prime=m^\prime\times c_{eau}}}\),

on a : \({\large { m^\prime=\dfrac{C^\prime}{c_{eau}}=\dfrac{167}{{4,18\cdot10}^3} \color{blue}=4,00\cdot 10^{-2}\ \mathrm{kg}=40,0\ \mathrm{g}}}\)

Glossaire

Adiabatique
Une transformation adiabatique (ou processus adiabatique) est une transformation qui ne produit pas d'échange de chaleur avec le milieu extérieur \(\left (Q = 0\right )\).
Ce type de transformation a lieu lorsque le système thermodynamique (dans ce cas un gaz parfait) se trouve dans un récipient isolé de l'extérieur par l'intermédiaire de parois adiabatiques. Les transformations qui se produisent très rapidement et pour lesquelles le système n'a pas le temps d'échanger de la chaleur avec le milieu extérieur peuvent elles aussi être considérées comme étant adiabatiques.
Capacité thermique
La capacité thermique d'un objet tient déjà compte de la masse de l'objet contrairement à la capacité thermique massique d'un corps.
La capacité thermique d'un objet est donc définie pour l'objet dans son entièreté . Quelque ce soit la masse de cet objet, sa capacité thermique tiendra donc déjà compte de sa masse.
Valeur en eau
La valeur en eau d'un objet est la masse d'eau équivalente à cet objet pour les transferts thermiques.
Par exemple, la valeur en eau d'un calorimètre et de ses accessoires correspond à la masse d'eau équivalente permettant de réaliser les même transferts thermiques.