Activité n°1 (Chap.1) : Les différents régimes d'écoulement en charge

Introduction

Dans le chapitre de la statique des fluides vu en 1ère année, les fluides étaient au repos dans le champ de pesanteur, ils étaient donc immobiles. Dans le cadre de la dynamique des fluides, les fluides ne sont plus en équilibre : ils sont en mouvement.

Attention :

Je vous conseille d'ouvrir une nouvelle fenêtre ou un nouvel onglet rien que pour les documents.

🔎 Notions préliminaires ⚓

Définition :

Les écoulements étudiés sont stationnaires : ils sont caractérisés par des grandeurs dont les valeurs restent constantes au cours du temps et en chaque point du fluide (mais peuvent être différentes entre deux points différents du fluide).

Complément :

La Fig.1 ci-contre montre que le régime permanent d'écoulement à la sortie d'un robinet se produit uniquement dans l'intervalle de temps $\left[5\ s\ ;\ 60\ s\right]$, alors que l'écoulement s'effectue dans l'intervalle $\left[2\ s\ ;\ 110\ s\right]$.

Attention :

On distingue les écoulements en charge, dans lesquels l'eau remplit complètement la canalisation (notamment les réseaux d'eau potable), des écoulements à surface libre pour lesquels il existe une interface entre l'eau et l'air (cas des rivières et des réseaux d'assainissement).

📚 Documents ⚓

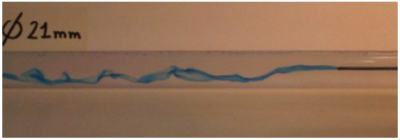
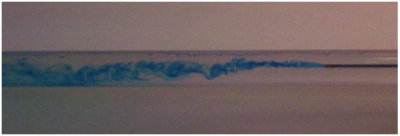
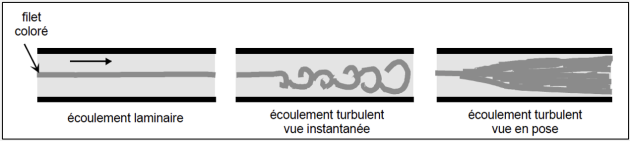
📄 Mise en évidence expérimentale des différents régimes d'écoulement dans une canalisation en charge - [Document n°1]⚓

Complément : Mise en évidence expérimentale des différents régimes d'écoulement dans une canalisation en charge - [Document n°1]

On injecte un colorant dans une canalisation remplie d'eau. Une vanne permet de contrôler le débit d'écoulement de l'eau dans la canalisation. Selon le débit imposé, on observe les photographies reproduites ci-contre :

📄 Les résultats de Reynolds - [Document n°2]⚓

Complément : Les résultats de Reynolds - [Document n°2]

Les expériences réalisées par Reynolds en 1883 sur l'écoulement d'un fluide dans une conduite cylindrique rectiligne ont montré l'existence de deux régimes d'écoulement : laminaire et turbulent.

En utilisant des fluides divers (de viscosités différentes), et en faisant varier le débit et le diamètre de la canalisation, Reynolds a montré que l'on pouvait déterminer le régime d'écoulement (laminaire ou turbulent) via l'estimation d'un nombre sans dimension, appelé nombre de Reynolds et noté ${Re}$, calculable à l'aide de la relation :

\[\fbox{$ {\Large {\color{blue} \text{ } Re =\dfrac{ \rho \ \mathrm{v} \ D }{ \eta } \text{ } } } $}\]

Avec :

$\rho$ : masse volumique en $\mathrm{kg.m^{-3}}$
$v$ : vitesse en $\mathrm{m.s^{-1}}$
$D$ : diamètre de la canalisation en $\mathrm{m}$
$\eta$ : viscosité dynamique^[*] du fluide.

Le nombre de Reynolds peut aussi se calculer à l'aide de la relation :

\[\fbox{$ {\Large {\color{blue} \text{ } Re =\dfrac{ \ \mathrm{v} \ D }{ \nu } \text{ } } } $}\]

Avec :

$\nu$ : viscosité cinématique^[*] du fluide.

Bien que la transition d'un régime d'écoulement à un autre se fasse progressivement, on considère généralement que l'écoulement est laminaire pour $Re<2000$, et que l'écoulement est turbulent pour$ Re>3000$. (Il faudra toujours tenir compte des consignes de l'énoncé).

📄 Équation aux dimensions - [Document n°3]⚓

Complément : Équation aux dimensions - [Document n°3]

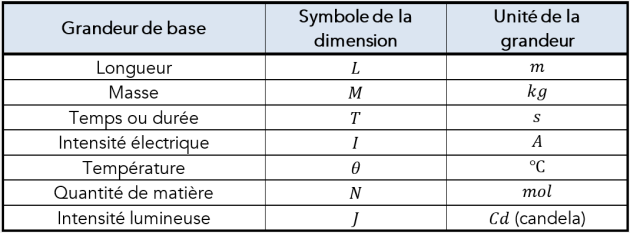
L'équation aux dimensions est la formule qui permet de déterminer la dimension dans laquelle doit être exprimé le résultat d'une formule. C'est une équation de grandeurs, c'est-à-dire dans laquelle on représente les phénomènes mesurés par un symbole : par exemple, une longueur est représentée par la lettre « $L$ ».

Grandeur de base

D'une manière générale il est possible d'exprimer la dimension de toutes les grandeurs physiques en fonction de sept dimensions de base. Les notations suivantes sont largement répandues :

Équation aux dimensions

L'équation aux dimensions est l'équation qui relie la dimension d'une grandeur dérivée à celles des sept grandeurs de base.

Dans une équation aux dimensions, la dimension de la grandeur dérivée $X$ est couramment notée $\left[X\right]$.

La forme générale d'une équation aux dimensions est : $\left[X\right]=L^\alpha \ M^\beta \ T^\gamma \ I^\delta \ \theta \ ^\epsilon \ N^\zeta \ J^\eta$

Où :

$L$, $M$, $T$, $I$, $\theta$, $N$, $J$ sont les dimensions respectives des sept grandeurs de base ;
$\ ^\alpha,\ \ ^\beta,\ \ ^\gamma,\ \ ^\delta,\ \ ^\varepsilon,\ \ ^\zeta,\ \ ^\eta$ sont les exposants respectifs des sept grandeurs de base.
Ces derniers sont appelés exposants dimensionnels.

📄 Viscosité cinématique de l'eau dans le domaine de température 5 °C – 65 °C - [Document n°4]⚓

Complément : Viscosité cinématique de l'eau dans le domaine de température 5 °C – 65 °C - [Document n°4]

(cliquer sur l'image pour l'agrandir)

📄 Profils de vitesses dans une canalisation - [Document n°5]⚓

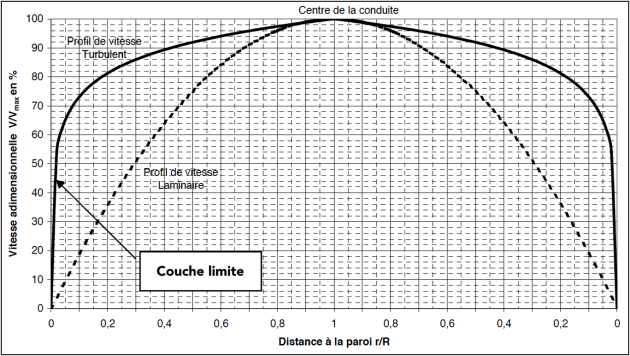
Complément : Profils de vitesses dans une canalisation - [Document n°5]

Les interactions dans l'écoulement sont différentes selon le régime d'écoulement (laminaire ou turbulent). À l'intérieur de la canalisation, on aura par conséquent une distribution différente des vitesses ponctuelles moyennées dans le temps (que l'on appelle vitesses moyennes temporelles) selon le régime d'écoulement.

La plupart des capteurs en réseau mesurent la vitesse moyenne temporelle en quelques points et reconstituent le profil complet de la vitesse. La connaissance du profil de vitesse dans une conduite permet alors de calculer le débit d'écoulement.

Le graphique ci-dessous compare la forme du profil de la vitesse en régimes laminaire et turbulent dans une conduite circulaire.

En abscisse est représenté le rapport entre la distance $\large r$ à la paroi et le rayon $\large R$ de la conduite. L'ordonnée représente le rapport, exprimé en pourcentage, entre la vitesse ponctuelle $\large v$ et la vitesse maximale $\large {v}_\mathrm{max}$ du profil.

On constate que la vitesse est maximale au centre de la canalisation. En revanche, le profil de vitesse en régime turbulent varie beaucoup plus qu'en laminaire au voisinage de la paroi, dans une zone appelée couche limite.

Sur le graphique :

Pour l'écoulement laminaire, la vitesse moyenne (dans une section droite de la canalisation) est de l'ordre de $\large {\dfrac{{v}_\mathrm{max}}{2}}$.
Pour l'écoulement turbulent, la vitesse moyenne est de l'ordre de $\large 0,8\times {v}_{max}$.

La vitesse moyenne $\large {v}_\mathrm{moy}$ sera définie comme la vitesse uniforme à travers la section $\large S$ qui assurerait le même débit que la répartition réelle des vitesses.

👨‍🎓 Questions préliminaires ⚓

Question⚓

Q1. (ANA) Déterminer, à l'aide d'une équation aux dimensions (voir Doc.3), la dimension et l'unité de la viscosité dynamique d'un fluide.

Solution ⚓

A1-Q1.

$\large \eta=\dfrac{\rho\ {v}\ D}{Re}$. L'équation aux dimensions s'écrit alors :

\[\begin{array}{rll} \large { \left[\eta \right] } & = & {\large { \dfrac{\left[ \rho \right] \times \left[ {v} \right] \times \left[ D \right] }{\left[ Re \right] } } } \\ & = & {\large { M.L^{-3}\times L.T^{-1}\times L } } \\ & = & {\large {{\color{blue} M.L^{-1}.T^{-1} }} } \end{array}\]

Question⚓

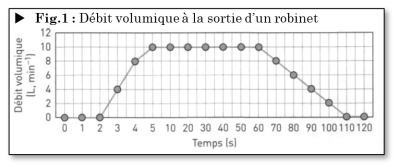
Q2. (ANA/RÉA) Dans l'expérience décrite dans le Doc.1, estimer la vitesse moyenne d'écoulement du fluide lorsque l'écoulement est laminaire puis lorsqu'il est turbulent.

Indiquer précisément les hypothèses que l'on est amené à faire pour mener à bien ces estimations.

Solution ⚓

A1-Q2.

On considère que l'écoulement est laminaire, donc d'après le Doc.2 on doit avoir un nombre de Reynolds tel que : $Re<2000$, c'est-à-dire :

$\large \dfrac{\rho\ {v}\ D}{\eta}<2000\ \ \ \ \ \ \mathrm{ou} \ \ \ \ \frac{{v}\ D}{\nu}<2000$

On cherche $v$ la vitesse d'écoulement :

on sait que le fluide est de l'eau donc $\rho=1\ 000\ \mathrm{kg.m^{-3}}$
on connaît le diamètre du tuyau : $D=21\ \mathrm{mm}=21\cdot{10}^{-3}\ \mathrm{m}$

Mais on ne connaît pas la viscosité dynamique $\large \eta$ ni la viscosité cinématique $\large \nu$.

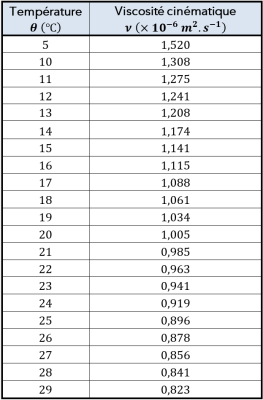
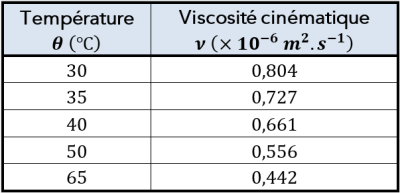
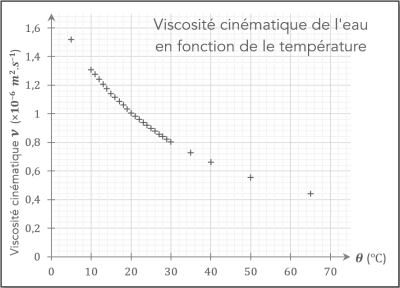
Cependant, le Doc.4 nous donne les valeurs de $\large \nu$ pour différentes températures pour l'eau.

On fera donc l'hypothèse que la température de l'eau est de $20\ \mathrm{^\circ C}$ (température ambiante).

On aura donc : $\large \nu=1,005\cdot{10}^{-6}\ \mathrm{m^2.s^{-1}}$.

Donc :

\[\begin{array}{rll} \large { v } & \large { < } & {\large { \dfrac{2000\ \times\ \nu}{D} } } \\ \large { v } & \large { < } & {\large { \dfrac{2000\ \times\ 1,005\cdot{10}^{-6}}{21\cdot{10}^{-3}} } } \\ \large { v } & \large { < } & {\large {{\color{blue} 9,6\cdot{10}^{-2}\ \mathrm{m.s^{-1}} }} } \\ \large { v } & \large { < } & {\large {{\color{blue} 9,6\ \mathrm{cm.s^{-1}} }} } \end{array}\]

Pour un écoulement turbulent, $Re>3000$, donc (toujours pour $20\ \mathrm{^\circ C}$), on a :

\[\begin{array}{rll} \large { \dfrac{v \ D}{\nu} > 3\ 000 } & \large { \Leftrightarrow } & {\large { {v} >\dfrac{3000\ \times\ \nu}{D} } } \\ & & {\large { {v}>\dfrac{3000\ \times\ 1,005\cdot{10}^{-6}}{21\cdot{10}^{-3}} } } \\ & & {\large {{ {v}> \color{blue}1,4\cdot{10}^{-1}\ \mathrm{m.s^{-1}} }} } \\ & & {\large {{ {v}> \color{blue}14\ \mathrm{cm.s^{-1}} }} } \end{array}\]

Question⚓

Q3. (ANA) Il est rare que l'on rencontre des situations d'écoulement laminaire dans les réseaux d'eau potable et d'assainissement. Le cas n'est toutefois pas totalement exclu. Déterminer les conditions dans lesquelles un tel écoulement peut être observé.

🔎 Investigation ⚓

Question⚓

Q4. (ANA) Le nombre de Reynolds fait intervenir la vitesse moyenne d'écoulement du fluide. Selon vous, qu'entend-on par « vitesse moyenne » d'écoulement ?

Question⚓

Q5. (ANA) Quelle est, selon vous, la répartition des vitesses dans une canalisation horizontale droite ?

Question⚓

Q6. (RÉA) Lancer l'animation « Pression du fluide et Flux » et sélectionner l'onglet « flux ».

L'animation peut être consulté en plus grand via ce lien : https://phet.colorado.edu/fr/simulation/fluid-pressure-and-flow

Q7. (ANA) Après vous être familiarisé avec la simulation, proposer un protocole expérimental exploitant la simulation et permettant de tester votre hypothèse.

✋ Appeler le professeur pour qu'il vérifie votre travail avant de passer à la suite ✋

Q8. (RÉA) Après validation de votre protocole, le mettre en œuvre et conclure.

Question⚓

Q9. (ANA) Que peut-on dire de la vitesse au centre de la canalisation ?

Question⚓

Q10. (ANA) Si on suppose que l'écoulement dans la conduite de la simulation est laminaire, quelle sera la vitesse moyenne de l'eau pour un débit de $5\ 000\ \mathrm{L/{s}}$\ ?

Glossaire

Viscosité cinématique
La viscosité cinématique $\nu$ (lettre grecque nu) est le quotient de la viscosité dynamique $\eta$ par la masse volumique du fluide $\rho$ :
$\nu = \dfrac{\eta}{\rho}$
Elle représente la capacité de rétention des particules du fluide et quantifie sa capacité à s'épancher.
Viscosité dynamique
La viscosité dynamique est une grandeur physique qui caractérise la résistance à l'écoulement laminaire d'un fluide incompressible. Les fluides newtoniens ont une viscosité dynamique indépendante du gradient de vitesse.

Elle est fortement dépendante de la température.

La viscosité dynamique est usuellement notée $\mu$ (lettre grecque mu) dans les ouvrages de mécanique des fluides, mais parfois elle est noté avec la lettre grecque eta $\eta$.

Plus d'info : https://fr.wikipedia.org/wiki/Viscosit%C3%A9_dynamique