🔎 Observations - [§A.]⚓
Complément : Mise en évidence des pertes de charges - [Document n°1]
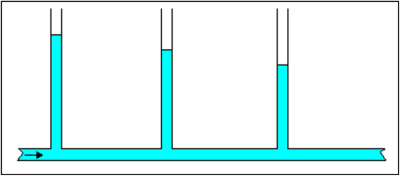
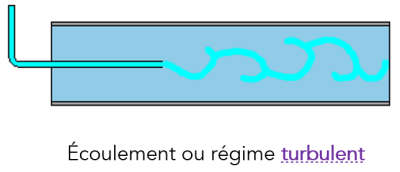
La pression d'un liquide réel diminue tout au long d'une canalisation dans laquelle il s'écoule, même si elle est horizontale et de section uniforme, contrairement au théorème de Bernoulli.
Dans la canalisation représentée ci-contre, le liquide se déplace de la gauche vers la droite. La hauteur de liquide dans un tube vertical est d'autant plus faible qu'il est à droite : la pression dans la canalisation est plus faible à droite.
La pression d'un fluide réel diminue après le passage à travers un coude, une vanne ou un rétrécissement
Définition à savoir 🚩
👨🎓 Les régimes d'écoulement : Nombre de Reynolds (Rappel) - [§B.]⚓
Complément : Régimes d'écoulement - [Document n°2]
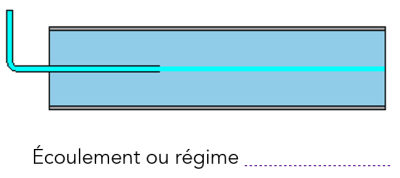
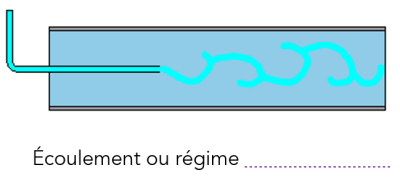
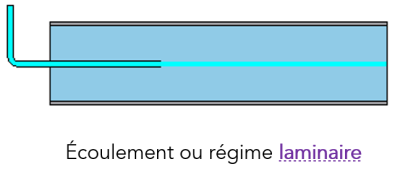
Les expériences réalisées par Reynolds (1883) lors de l'écoulement d'un liquide dans une conduite cylindrique rectiligne dans laquelle arrive également un filet de liquide coloré, ont montré l'existence de deux régimes d'écoulement : laminaire et turbulent.
Petite vidéo d'une reproduction de l'expérience de Reynolds : 01 - Act.n°5 - VIDEO - Laminar Flow then Turbulent Flow.mp4 
Complément : Le nombre de Reynolds - [Document n°3]
En utilisant des fluides divers, en faisant varier le débit et le diamètre de la canalisation, Reynolds a montré que le paramètre qui permettait de déterminer si l'écoulement est laminaire ou turbulent est un nombre sans dimension appelé « nombre de Reynolds » et donné par :
Avec :
\(\large \rho\) : masse volumique en \(\mathrm{kg.m^{-3}}\)
\(\large v\) : vitesse en \(\mathrm{m.s^{-1}}\)
\(\large D\) : diamètre de la canalisation en \(\mathrm{m}\)
\(\large \eta\) : viscosité dynamique[*] du fluide
\(\large \nu\) : viscosité cinématique[*] du fluide.
En fonction de la valeur de \(Re\), l'écoulement sera soit laminaire, soit intermédiaire, soit turbulent.
Définition à savoir 🚩
Attention : Remarque :
Les valeurs limite du nombre de Reynolds de \(2\ 000\) et \(3\ 000\) définissants les différents régimes d'écoulement sont celles que l'on adopte généralement, mais ces valeurs ne sont pas strictes. On peut trouver dans la littérature des valeurs différentes suivant les sources et auteurs. Pour la limite entre écoulement laminaire et intermédiaire, les valeurs sont assez proches : autour de \(2\ 000-2\ 100\). En revanche, pour la limite entre écoulement intermédiaire et turbulent, des valeurs très différentes peuvent être indiquées : les valeurs de \(3\ 000\), \(4\ 000\) ou \(10\ 000\) sont souvent retrouvées.
👨🎓 Les pertes de charges - [§C.] - Documents utiles pour les exercices⚓
📄 Les différentes causes - [Document n°4]⚓
Complément : Les différentes causes - [Document n°4]
Lorsque l'on considère un fluide réel, les pertes de charge dépendent de la forme, des dimensions et de la rugosité de la canalisation, de la vitesse d'écoulement et de la viscosité du liquide mais pas de la valeur absolue de la pression qui règne dans le liquide.
La différence de pression due aux pertes de charge \(\Delta P_{1-2}=p_1-p_2\) entre deux points (1) et (2) d'un circuit hydraulique a pour origine :
Les frottements du fluide sur la paroi interne de la tuyauterie et entre les couches de fluide : on les appelle pertes de charge régulières ou systématiques (elles se répartissent régulièrement le long de la canalisation).
La résistance à l'écoulement provoquée par les accidents de parcours (vanne, coude, rétrécissement, élargissement, clapet, capteur, organe de mesure de vitesse, de débit, ...) : on les appelle pertes de charge accidentelles ou singulières.
📄 Détermination des pertes de charges - [Document n°5]⚓
Complément : Détermination des pertes de charges - [Document n°5]
Les pertes de charge apparaissent dans la loi de Bernoulli (voir Activité n°6), qui peut donc être appliquée pour calculer les pertes de charge. Il faut alors cependant disposer de toutes les informations nécessaires, à savoir vitesse du fluide, pression et altitude pour chacune des deux sections entre lesquelles on veut calculer les pertes de charge.
Ainsi, la plupart du temps, on a recours à des relations empiriques et/ou abaques pour estimer les pertes de charge.
Les pertes de charge régulières et singulières sont estimées séparément, puis sommées pour obtenir les pertes de charge totales :
📄 Les pertes de charges régulières ou linéaires - [Document n°6]⚓
Complément : Les pertes de charges régulières ou linéaires - [Document n°6]
Les pertes de charge régulières (ou linéaires) \(\Delta P_\text{rég}\) dépendent de la vitesse du fluide, de sa viscosité, de la géométrie de la conduite (diamètre, longueur) et de sa rugosité (hauteur des aspérités sur la paroi interne de la conduite). Elles sont calculées suivant l'expression :
Avec :
\(\large \lambda\) : coefficient de pertes de charges linéaire sans unité (noté également \(\large f\) dans la fiche annexe), il dépend du régime d'écoulement, donc du nombre de Reynolds \(\large Re\)
\(\large \rho\) : masse volumique du fluide, exprimée en \(\mathrm{kg.m^{-3}}\)
\(\large v\) : vitesse moyenne du fluide, exprimée en \(\mathrm{m.s^{-1}}\)
\(\large \ell\) : longueur de la canalisation, exprimée en \(\mathrm{m}\)
\(\large D\) : diamètre de la canalisation, exprimée en \(\mathrm{m}\)
📄 Le coefficient de pertes de charge λ - [Document n°7]⚓
Complément : Le coefficient de pertes de charge λ - [Document n°7]
Le coefficient de pertes de charge \(\large \lambda\) dépend du régime d'écoulement du fluide. Il est déterminé soit à l'aide de relations empiriques, soit à l'aide d'abaques, en fonction du nombre de Reynolds \(Re\) et de la rugosité relative de la conduite \({\varepsilon}/{D}\) (dans le cas d'un écoulement en régime turbulent rugueux).
\(\large \varepsilon\) : hauteur moyenne des aspérités \(\left(\mathrm{en \ m}\right)\) ; \(\large D\) : diamètre interne de la conduite \(\left(\mathrm{en \ m}\right)\)
On trouve dans la littérature diverses relations empiriques pour déterminer \(\large \lambda\) en fonction du régime d'écoulement. Les plus utilisées sont données ci-après :
Régime laminaire \(\large \left(\ Re<2\ 000\ \right)\) : \(\lambda=\frac{64}{Re}\) (On peut retrouver cette valeur avec l'abaque de Moody).
Régime turbulent lisse \(\large \left(\ 2\ 000 < Re < 10^4 \ \right)\) : (relation de Blasius) \(\large \lambda=0,316\times Re^{-0,25}\)
Régime turbulent rugueux \(\large \left(\ Re>{10}^4 \ \right)\) : il existe différentes relations empiriques, mais l'utilisation d'un abaque est plus commode dans ce cas (comme l'abaque de Moody).
Divers abaques pour la détermination de \(\large \lambda\) sont également disponibles dans la littérature, les plus classiques étant les abaques de Colebrook et de Moody. Un exemple d'abaque de Moody vous a été donné lors de l'activité n°4.
📄 Les pertes de charges singulières - [Document n°8]⚓
Complément : Les pertes de charges singulières - [Document n°8]
Les pertes de charge singulières (ou ponctuelles) \(\Delta P_\text{sing}\) sont liées à la présence d'élément ou accident sur la conduite (vanne, coude, rétrécissement, élargissement, clapet, capteur, organe de mesure de vitesse, de débit etc...). Elles sont calculées suivant l'expression :
Avec :
\(\large K\) : coefficient dépendant du type d'accident (à chercher dans la littérature)
\(\large \rho\) : masse volumique du fluide, exprimée en \(\mathrm{kg.m^{-3}}\)
\(\large v\) : vitesse moyenne du fluide, exprimée en \(m.s^{-1}\)
Le coefficient \(K\) correspond à l'accident considéré. Sa valeur est à chercher dans la littérature ou dans les documents fournis par les constructeurs.
Il est souvent plus pratique d'exprimer les pertes de charge ponctuelles en utilisant la notion de longueur équivalente \(\ell_\text{éq}\). Cela signifie que l'accident considéré provoque une perte de charge équivalente à celle provoquée par une longueur \(\ell_\text{éq}\) de conduite (de même caractéristiques que celle sur laquelle est placé l'accident). La longueur équivalente peut est calculée comme suit :
Certains abaques fournissent directement la valeur de longueur équivalente.
Ainsi, pour calculer les pertes de charges totales (linéaires + ponctuelles), on pourra ajouter toutes les longueurs équivalentes correspondant aux accidents \(\large \sum \ell_\text{éq}\) à la longueur de conduite simple \(\ell\), ce qui simplifie les calculs :
❔ Questions⚓
Question⚓
Q5. (ANA/APP) Quel est alors le signe de \(\Delta P_{1-2}\) ? Est-ce bien en accord avec la relation de Bernoulli avec pertes de charges suivante ? (voir Activité n°6 pour l'équation de Bernoulli)
Solution⚓
A5-Q5.
\(\Delta P_{1-2}=p_1-p_2>0\). C'est en accord avec la relation de Bernoulli avec pertes de charges, car le fluide perd de l'énergie en se déplaçant à cause des pertes de charges, on a donc :
Énergie du fluide à la section 1 supérieure à Énergie du fluide à la section 2
Il faut donc un terme qui compense cette perte d'énergie du coté 2 de le relation, \(\Delta P_{1-2}\) doit bien être positif.
Question⚓
Q6. (ANA/APP) La notation avec la lettre \(\large \Delta\) signifie-t-elle réellement une variation au sens stricte du terme ?
🏋️♂️ Exercices pour s'entraîner⚓
💪 Exercice n°1 : Installation hydroélectrique⚓
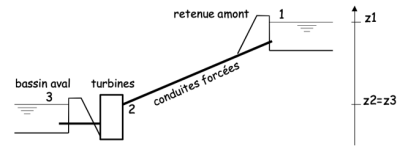
Une installation hydroélectrique comporte une retenue d'eau amont, trois conduites forcées parallèles de diamètre \(D=300\ \mathrm{cm}\) chacune, un ensemble de turbines, un bassin aval selon le schéma donné en annexe. Lors du turbinage, le débit-volume total est \(q_\mathrm{V}=217 \ \mathrm{m^{3}.s^{-1}}\).
On supposera nulles les vitesses de l'eau en 1 et en 3.
Complément : Données :
Viscosité cinématique de l'eau : \(\nu=1,00\cdot{10}^{-6}\ \mathrm{m^{2}.s^{-1}}\)
\(p_1=\ p_3=1\ 100\ \mathrm{mbar}\)
\(p_2=73\ \mathrm{bar}\)
\(z_1=1\ 695\ \mathrm{m}\)
\(z_2=z_3=740\ \mathrm{m}\)
Question⚓
Q7. (RÉA) Calculer la vitesse d'écoulement de l'eau dans les conduites forcées.
Aide : Utiliser le débit volumique et la définition de la surface. Réponse : \(v=30,7\ \mathrm{m.s^{-1}}\).
Solution⚓
A5-Q7.
Question⚓
Q8. (RÉA) Calculer le nombre de Reynolds pour l'écoulement de l'eau dans une conduite forcée ; l'écoulement est-il laminaire ou turbulent ?
Aide : Comparer par rapport aux valeurs de 3 000 et 2 000. Réponse : \(Re=9,21\cdot{10}^7\).
💪 Exercice n°2 : Pipe-Line⚓
Un pipe-line de \(50,0\ \mathrm{cm}\) de diamètre intérieur est destiné à transporter du pétrole brut de viscosité dynamique \(\eta=0,27\ \mathrm{Pa.s}\) et de masse volumique \(900\ \mathrm{kg.m^{-3}}\) avec un débit-masse de 350 tonnes par heure. Des stations de pompage sont régulièrement réparties le long de la conduite ; chaque pompe augmente la pression de \(4,5\ \mathrm{bar}\) et est actionnée par un moteur de rendement 75 %.
Question⚓
Q9. (RÉA) Déterminer l'expression de la vitesse du pétrole brut en fonction de débit massique, de la masse volumique et du diamètre de la canalisation. Puis calculer sa valeur. ?
Aide : Utiliser la relation entre le débit massique et volumique, puis celle entre le débit volumique et la section. Vous devrez obtenir \(v=\frac{4\ Q_m}{\rho\times\pi\times D^2}\). Réponse : \(v=0,550\ \mathrm{m.s^{-1}}\).
Solution⚓
A5-Q9.
Question⚓
Q10. (RÉA) Déterminer l'expression du nombre de Reynolds en fonction du débit massique, du diamètre de la canalisation et de la viscosité dynamique, puis calculer sa valeur. Puis en déduire le type de cet écoulement.
Aide : Il faut injecter la formule de la vitesse de la question précédente dans la formule du nombre de Reynolds pour obtenir \(Re=\frac{4\ Q_m}{\pi\times D\times\eta}\). Réponse : \(Re\approx 920\).
Solution⚓
A5-Q10.
\(\large { Re=\dfrac{\rho\ v \ D}{\eta}=\dfrac{\rho\times\dfrac{4\ Q_m}{\rho\times\pi\times D^2}\times D}{\eta}=\dfrac{\dfrac{4\ Q_m}{\pi\times D}}{\eta} }\)
Question⚓
Q11. (RÉA ) Déterminer les pertes de charges régulières (ou linéaires) pour une conduite de \(500\ \mathrm{m}\) de longueur.
Aide : Déterminer \(\lambda\) avec une formule si l'écoulement est laminaire. Réponse : \(\Delta P_\text{rég}=9,5\ \mathrm{kPa}\).
Solution⚓
A5-Q11.
\(\large \Delta P_\text{rég}=\lambda \times \dfrac{\rho \times \ell \times v^2 }{2\times D}\)
Comme on est en régime laminaire, on peut calculer le coefficient de frottement avec : \(\lambda=\dfrac{64}{Re}\).
\(\large \Delta P_\text{rég}=\dfrac{64}{Re}\times\dfrac{\rho\times\ell\times v^2}{2\times D}\)
\(\large \Delta P_\text{rég}=\dfrac{64}{9,2\cdot{10}^2}\times\dfrac{900\times500\times\left(0,550\right)^2}{2\times50,0\cdot{10}^{-2}}\)
\(\large\color{blue}\Delta P_\text{rég}=9,5\cdot{10}^3\ \mathrm{Pa}\)
Remarque :
Ou peut calculer les pertes de charges grâce à la loi de Poiseuille (voir Doc.9 plus loin (ouvrir dans un nouvel onglet)).
Question⚓
Q12. (ANA/RÉA) Puis calculer la distance maximale entre deux stations de pompage permettant l'écoulement du pétrole.
Aide : Que doivent valoir les pertes de charges maximales pour que le pétrole puisse s'écouler entre 2 pompes ? Utiliser cette valeur avec la formule du Doc.6). Réponse : \(\ell=23,8\ km \).
Solution⚓
A5-Q12.
La première pompe va fournir une pression de \(\large 4,5\ bar=4,5\cdot{10}^5\ \mathrm{Pa}\). La distance maximale que pourra parcourir le pétrole en s'écoulant devra être tel que les pertes de charges régulières soient inférieures à \(\large4,5\cdot{10}^5\ \mathrm{Pa}\). Notons cette valeur \(\large \Delta P_\text{rég max}=4,5\cdot 10^5 \ \mathrm{Pa}\).
Calculons donc la distance pour avoir \(\large \Delta P_\text{rég} < \large \Delta P_\text{rég max}\)
Question⚓
Q13. (RÉA/APP) Réécrire l'équation de poiseuille de manière à avoir le débit volumique \(q_{\mathrm{V}}\) en fonction du rayon de la canalisation, de la viscosité dynamique, de la longueur de la canalisation et des pertes de charges.
Solution⚓
A5-Q13.
📄 Les pertes de charges singulières - [Document n°9]⚓
Complément : Écoulement laminaire en conduite cylindrique : loi de Poiseuille - [Document n°9]
Pour un écoulement laminaire, l'équation de Poiseuille donne la vitesse du fluide en fonction du rayon auquel on se place dans la conduite. Elle traduit le profil parabolique des vitesses.
À partir de cette équation, on peut exprimer la vitesse moyenne du fluide au sein de la conduite sur une longueur \(\large \ell\) donnée :
Avec :
\(\large R\) : Rayon de la canalisation cylindrique en \(\mathrm{m}\) ;
\(\large \eta\) : viscosité dynamique du fluide exprimée en \(\mathrm{Pa.s}\) ;
\(\large \ell\) : longueur de la canalisation, exprimée en \(\mathrm{m}\) ;
\(\large v\) : vitesse moyenne du fluide, exprimée en \(\mathrm{m.s^{-1}}\) ;
\(\large \Delta P\) : pertes de charges telles que \(\large \Delta P=p_\text{entrée} - p_\text{sortie}\)
💪 Exercice n°3 : Une histoire de viscosité⚓
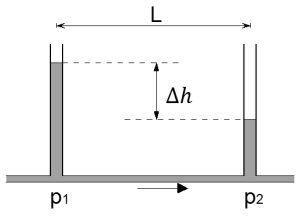
Pour mesurer la viscosité d'une huile, on utilise le dispositif schématisé ci-contre. On fait couler l'huile dans un tube horizontal de \(7,0\ \mathrm{mm}\) de diamètre et comportant deux tubes manométriques verticaux situés à \(L=600\ \mathrm{mm}\) de l'un de l'autre.
On règle le débit-volume de cet écoulement à \(4,0⋅10^{-6}\ \mathrm{m^{3}/s}\).
La dénivellation de l'huile entre ces deux tubes est alors \(\Delta h=267\ \mathrm{mm}\).
La variation de pression dans le tube horizontale s'exprime : \({\Delta P}=p_1-p_2\).
La masse volumique de l'huile est de \(910\ {kg}/{m^3}\) .
On suppose que l'écoulement est de type laminaire. On prendra \(g=9,81\ \mathrm{m.s^{-2}}\).
Question⚓
Q14. (ANA/RÉA) Calculer la viscosité dynamique de l'huile.
Aide : Utiliser la loi de Poiseuille de la Q13, en utilisant le principe fondamental de l'hydrostatique pour déterminer l'expression des pressions p_1 et p_2 par rapport à la pression atmosphérique qui est au niveau des surfaces libres des fluides en haut des tubes manométriques et déterminer \({\Delta P}=p_1-p_2\).
Réponse : \(\eta=5,85\cdot{10}^{-2}\ \mathrm{Pa.s}\).
Solution⚓
A5-Q14.
On utilise la loi de Poiseuille car l'écoulement est supposé laminaire. On peut utiliser la formule de la question Q13.
\(\large \eta=\dfrac{\pi\times R^4}{8\cdot q_V\cdot L}\cdot\Delta P\) Il faut déterminer \(\Delta P=p_1-p_2\).
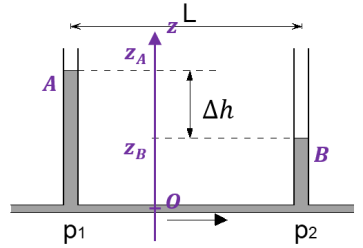
On définit un axe des altitudes avec un point A et B comme indiqués sur le schéma. On a alors \(z_1=z_2=0\) et \(\Delta h=z_{\mathrm{A}}-z_{\mathrm{B}}\) et \(p_{\mathrm{A}}=p_{\mathrm{atm}}=p_{\mathrm{B}}\).
On applique le principe fondamental de l'hydrostatique entre 1 et A, on a :
\(\large p_1+\rho\cdot g\cdot z_1=p_A+\rho\cdot g\cdot z_{\mathrm{A}}\)
\(\color{blue} p_1=p_{\mathrm{atm}}+\rho\cdot g\cdot z_{\mathrm{A}}\)
Avec le même raisonnement entre 2 et B :
\(\color{blue} p_2=p_{\mathrm{atm}}+\rho\cdot g\cdot z_{\mathrm{B}}\)
On a donc :
Question⚓
Q15. (ANA/RÉA) Calculer le nombre de Reynolds de cet écoulement. Justifier l'hypothèse initiale.
Aide : Il faut partir de la formule dans le document n°3 puis déterminer la formule de calcul de \(Re\) qui sera : \(Re=\frac{4\times\rho\times q_V}{\eta\times\pi\times D}\)
Réponse : \(Re=11,3\).
Solution⚓
A5-Q15.
\(\large \color{blue} Re\ll2\ 000\) donc l'écoulement est bien laminaire. L'hypothèse initiale est donc valide.
💪 Exercice n°4 : Le robinet de jardin⚓
Un robinet de jardin a été installé à \(50\ \mathrm{m}\) de l'arrivée principale d'eau où la pression vaut \(3,0\ \mathrm{bar}\).
Le tuyau de raccordement utilisé pour rejoindre le robinet de jardin a un diamètre intérieur standard de \(1,0\ \mathrm{cm}\).
Le débit volumique souhaité est de \(0,40\ \mathrm{L / s}\). La viscosité de l'eau est \(\eta={10}^{-3}\ \mathrm{Poiseuille}\).
Question⚓
Q16. (ANA/RÉA) Évaluer la perte de charge pour cet écoulement de Poiseuille laminaire. Commenter.
(Réponse : \(\Delta P=0,81\ \mathrm{bar}\).)
Solution⚓
A5-Q16.
Les pertes de charges ne sont pas négligeables compte tenu de la pression d'arrivée d'eau qui vaut \(3\ \mathrm{bar}\).
💪 Exercice n°5 : Pertes de charges⚓
On considère une conduite de longueur \(L=10\ \mathrm{m}\) et de diamètre \(D=10\ \mathrm{cm}\) dans laquelle circule une huile de viscosité \(\nu=50\cdot 10^{-6}\ \mathrm{m^2.s^{-1}}\) et de masse volumique \(\rho=865\ \mathrm{kg.m^{-3}}\).
Question⚓
Q17. (ANA/RÉA) Calculer les pertes de charge dans cette conduite pour un débit volumique \(q_{\mathrm{V}}=20\ \mathrm{m^3.h^{-1}}\).
(Aide : Calculer la vitesse, puis le nombre de Reynolds, puis déterminer \(\lambda\) puis enfin \(\Delta P_\mathrm{tot}\).)
(Réponse : \(v=7,1\cdot{10}^{-1}\ \mathrm{m.s^{-1}}\) et \(\Delta P_\mathrm{tot}=1,0\cdot{10}^3\ \mathrm{Pa}\))
Solution⚓
A5-Q17.
Dans ce cas, pas d'accident sur la conduite. Les pertes de charges totales ne sont que des pertes de charge linéaires :
\(\large \Delta P_\mathrm{tot}=\Delta P_\text{rég}=\lambda\times\dfrac{\rho\times L\times v^2}{2\times D}\)
Pour déterminer la valeur de \(\large \lambda\), il faut connaître le régime d'écoulement.
\(\large Re=\dfrac{\rho\times v\times D}{\eta}=\dfrac{v\times D}{\nu}\) avec \(\large v=\dfrac{4\times q_{\mathrm{V}}}{\pi\times D^2}=\dfrac{4\times\dfrac{20}{3\ 600}}{\pi\times\left(0,1\right)^2}=7,1\cdot{10}^{-1}\ \mathrm{m.s^{-1}}\)
\(\large Re=\frac{7,1\cdot{10}^{-1}\times10\cdot{10}^{-2}}{50\cdot{10}^{-6}}\)
\(\large \color{blue} Re=1,4\cdot{10}^3\)
\(\large Re<2\ 000\), le régime d'écoulement est donc laminaire, et on peut déterminer \(\large \lambda\) comme suit :
\(\large \lambda=\dfrac{64}{Re}=\frac{64}{1,4\cdot{10}^3} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \color{blue} \lambda =4,6\cdot{10}^{-2}\)
Donc :
\(\large \Delta P_\mathrm{tot}=4,6\cdot{10}^{-2}\times\dfrac{865\times10\times\left(7,1\cdot{10}^{-1}\right)^2}{2\times10\cdot{10}^{-2}}\)
\(\large \color{blue} \Delta P_\mathrm{tot}=1,0\cdot{10}^3\ \mathrm{Pa}\)
Question⚓
Q18. (ANA/RÉA) Même question avec un débit de \(40\ \mathrm{m^3.h^{-1}}\).
(Aide : Raisonner en comparant le débit volumique de cette question avec celui de la précédente. Que devient la vitesse ? Le nombre de Reynolds ? Calculer le coefficient de frottement puis \(\Delta P_\mathrm{tot}\).)
(Réponse : \(v=1,4\ \mathrm{m.s^{-1}}\) et \(\Delta P_\mathrm{tot}=3,6\cdot{10}^3\ \mathrm{Pa}\))
Solution⚓
A5-Q18.
Il y a un changement de débit, donc de vitesse du fluide, et potentiellement du régime d'écoulement. Le débit est doublé, donc la vitesse aussi, vu que la canalisation n'a pas changée : \(\large v=1,4\ \mathrm{m.s^{-1}}\)
De même, le nombre de Reynolds est lui aussi doublé : \(\large Re=2,8\cdot{10}^3\).
\(\large 2\ 000<Re<10\ 000\), le régime d'écoulement est donc turbulent lisse, et on peut déterminer \(\large \lambda\) comme suit :
On utilise la formule du Document n°7 : \(\large \lambda=0,316\times Re^{-0,25}\)
\(\large \lambda=0,316\times\left(2,8\cdot{10}^3\right)^{-0,25}=4,3\cdot{10}^{-2}\)
Donc :
\(\large \Delta P_\mathrm{tot}=4,3\cdot{10}^{-2}\times\dfrac{865\times10\times\left(1,4\right)^2}{2\times10\cdot{10}^{-2}}\)
\(\large \color{blue} \Delta P_\mathrm{tot}=3,6\cdot{10}^3\ \mathrm{Pa}\)
Question⚓
Q19. (ANA/RÉA) Pour \(q_V=40\ \mathrm{m^3.h^{-1}}\), calculer les pertes de charge engendrées si l'on insère sur cette conduite un robinet-vanne ouvert à \(25\ \%\) : \(K=1,8\). Calculer la longueur de conduite équivalente à cet élément.
(Aide : Calculer \(\Delta P_\mathrm{sing}\) (formule du Document n°8) puis \(\Delta P_\mathrm{tot}\) et enfin \(\ell_\text{éq}\).)
(Réponse : \(\Delta P_\mathrm{sing}=1,5\cdot{10}^3\ \mathrm{Pa}\) et \(\ell_\text{éq}\approx 4,1\ \mathrm{m}\))
Solution⚓
A5-Q19.
Ajout sur la conduite d'un robinet vanne ouvert à \(\large 25\ \%\) : \(K=1,8\)
Calcul des pertes de charge ponctuelles :
\(\large\Delta P_\text{sing}=K\times\dfrac{\rho\times v^2}{2}\)
\(\large\Delta P_\text{sing}=1,8\times\dfrac{865\times\left(1,4\right)^2}{2}\)
\(\large \color{blue} \Delta P_\text{sing}=1,5\cdot{10}^3 \mathrm{Pa} \\\)
Calcul des pertes de charge totales :
\(\large\Delta P_\text{tot}=\Delta P_\text{rég}+\Delta P_\text{sing}\)
\(\large\Delta P_\text{tot}=3,6\cdot{10}^3\ +1,5\cdot{10}^3\)
\(\large \color{blue} \Delta P_\text{tot}=5,1\cdot{10}^3 \mathrm{Pa} \\\)
Calcul de la longueur équivalente au robinet-vanne ouvert à \(\large 25\ \%\) :
\(\large \ell_\text{éq}=\dfrac{2\times D\times \Delta P_\text{sing}}{\lambda\times\rho\times v^2}\)
\(\large \ell_\text{éq}=\dfrac{2\times10\cdot{10}^{-2}\times1,5\cdot{10}^3}{4,3\cdot{10}^{-2}\times865\times\left(1,4\right)^2}\)
\(\large \color{blue} \ell_\text{éq}=4,1\ \mathrm{m}\)